Properties of 3D Shapes - Year 7 PDF Download
Key points
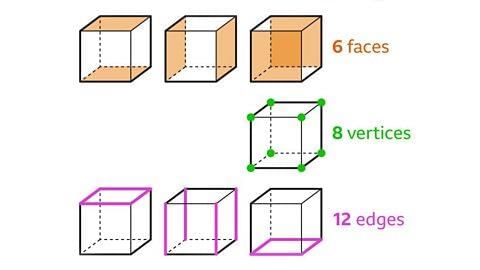 Image caption
Image captionSix Faces of a Cube
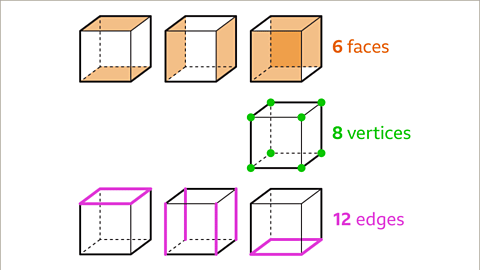
A cube has six faces. For example, imagine a dice. Each side of the dice is a face of the cube.
Eight Vertices of a Cube
A cube has eight vertices or corners. Picture each corner of a cube marked with a dot.
Twelve Edges of a Cube
A cube possesses twelve edges. Consider the edges of a Rubik's Cube, there are twelve of them.
- Definition of 2D Shapes:
- A polygon is a closed 2D shape with straight edges, defined by its length and width.
- Definition of 3D Shapes:
- A polyhedron is a closed 3D shape with polygonal faces, straight edges, and pointed vertices. Regular polyhedra are platonic solids.
- Examples of polyhedra include:
- Prism: A 3D shape with a constant polygon cross-section.
- Pyramid: A 3D shape with a polygon-shaped base and a pointed apex, named by the shape of its base.
- Platonic Solids: Polyhedra with regular polygon faces like tetrahedron, cube, octahedron, dodecahedron, and icosahedron.
- Properties of Polyhedra:
- A polyhedron is defined by its face (flat surfaces), edge (lines where faces meet), and vertex (corners).
- The number of edges in a polyhedron is two less than the sum of vertices and faces, given by the formula: \(E = V + F - 2\).
- Non-Polyhedral 3D Shapes:
- Cylinder: A 3D shape with a constant circular cross-section along its length.
- Cone: A 3D shape with a flat base and a curved surface tapering to a point at the top.
- Sphere: A round 3D shape with no edges, entirely made of curved surfaces.
Understanding 3D Shapes
A polyhedron is a closed 3D shape with polygonal faces, straight edges, and sharp vertices. Regular polyhedra are known as platonic solids.
- Polyhedron
- Prism
- Pyramid
- Platonic Solid
Definitions and Examples
- Polyhedron: A closed 3D shape with polygonal faces, straight edges, and sharp vertices.
- Prism: A 3D shape with a constant polygon cross-section.
- Pyramid: A 3D shape with a polygon-shaped base and a pointed apex.
- Platonic Solid: A polyhedron with regular polygon faces.
Properties of Polyhedra
- The properties of a polyhedron are characterized by its faces, edges, and vertices. The number of edges in a polyhedron is two less than the sum of its vertices and faces, given by the formula V - E + F = 2.
Geometric Shapes and Terminology
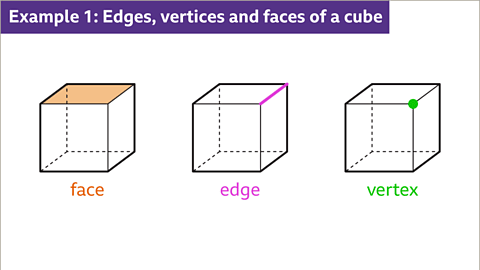
- Face: One of the flat surfaces of a solid shape.
- Edge: The line formed by joining two vertices of a shape. It's the line where two faces meet.
- Vertex: The point where two or more lines intersect or the corner of a shape. The plural form is vertices.
3D Shapes Classification
- 3D shapes that are non-polyhedral include:
- Cylinder: A 3D shape with a constant circular cross-section along its length.
- Cone: A 3D shape with a flat base and a curved surface extending to a point at the top.
- Sphere: A round 3D shape without edges.
- These 3D shapes have at least one curved surface and a face that is not a polygon.
Examples of 3D Shapes
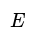 | 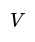 | 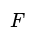 |
Cylinder
- A cylinder is a 3D shape with a constant circular cross-section across its length.
Cone
- A cone is a 3D shape with a flat base at the bottom and a curved surface reaching to a point at the top.
Sphere
- A sphere is a round 3D shape with no edges.
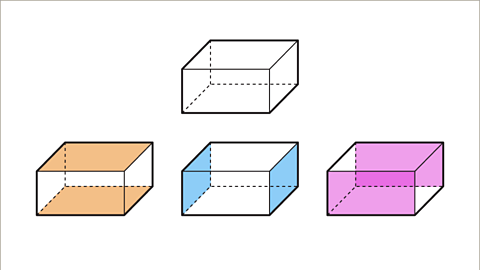
Cube
A cube is a 3D shape with six faces, eight vertices, and twelve edges. Each face of a cube is a square.
| Property | Number |
|---|---|
| Faces | 6 |
| Vertices | 8 |
| Edges | 12 |
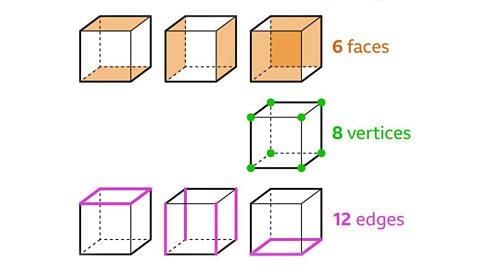 Image captionBack to top
Image captionBack to topUnderstanding 3D shapes
A three-dimensional shape characterized by straight edges and flat faces is known as a polyhedron. Shapes with curved surfaces do not fall under this category.
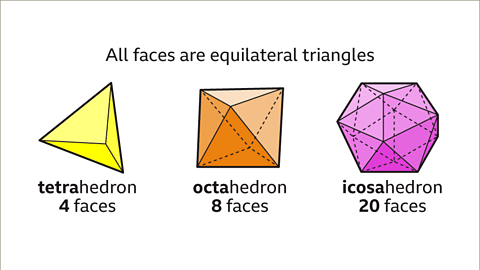
- The Platonic Solids - Regular Polyhedra:
- Tetrahedron: A solid with four equilateral triangle faces.
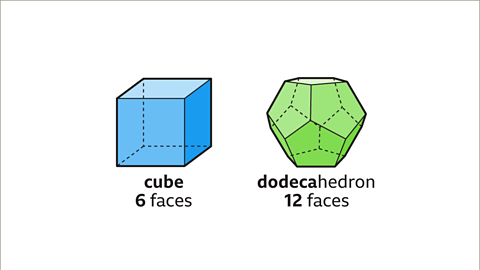
- Cube: A shape featuring six square faces.
- Octahedron: Solid with eight equilateral triangle faces.
- Dodecahedron: Featuring twelve pentagonal faces.
- Icosahedron: Exhibiting 20 equilateral triangular faces.
- All faces are regular polygons of the same size and shape, making them congruent.
- Each vertex has an equal number of faces meeting.
- Other Polyhedra:
- Cuboid: A three-dimensional shape with six rectangular faces, where opposite faces are congruent.
- Prisms: These shapes have a constant cross-section.
- Pyramids: Three-dimensional structures with a polygonal base connected to an apex.
- Non-Polyhedral 3D Shapes:
- Cylinders
- Cones
- Spheres
The Platonic Solids - Regular Polyhedra
The Platonic solids are a series of regular polyhedra, each with unique characteristics:
- Tetrahedron: A solid featuring four equilateral triangle faces.
- Cube: A shape composed of six square faces.
- Octahedron: A polyhedron with eight equilateral triangle faces.
- Dodecahedron: A solid having twelve pentagonal faces.
- Icosahedron: A shape with 20 equilateral triangular faces.
Tetrahedron
- A tetrahedron is a platonic solid characterized by four equilateral triangle faces.
- Each face of a tetrahedron is an equilateral triangle.
- For instance, a pyramid with a triangular base is a tetrahedron.
Cube
- A cube is a three-dimensional shape composed of six square faces.
- All angles in a cube are right angles, making it a regular polyhedron.
- For example, a standard dice is a cube.
Octahedron
- An octahedron is a platonic solid with eight equilateral triangle faces.
- Each face of an octahedron is an equilateral triangle.
- One can imagine two square-based pyramids placed base to base to visualize an octahedron.
Dodecahedron
- A dodecahedron is a platonic solid featuring twelve pentagonal faces.
- Each face of a dodecahedron is a regular pentagon.
- A soccer ball closely resembles a dodecahedron in shape.
Icosahedron
- An icosahedron is a platonic solid with 20 equilateral triangular faces.
- Each face of an icosahedron is an equilateral triangle.
- One can think of a 20-sided die as an approximation of an icosahedron.
Characteristics
- All the faces of these platonic solids are regular polygons.
- This means that each face has equal sides and equal angles.
- Regular polygons are polygons with all sides and angles congruent.
Characteristics of Polyhedra
- All the faces of polyhedra are congruent, meaning they are identical in shape and size.
- The same number of faces meet at each vertex of a polyhedron.
Types of Polyhedra
- Cuboid: A type of polyhedron with six rectangular faces. The opposite faces of a cuboid are congruent.
- Prisms: Polyhedra with a constant cross-section, similar to a rectangular prism.
- Pyramids: Polyhedra with a polygonal base connected to an apex, which is the peak of the pyramid.
Examples of Polyhedra
- Cuboid: Think of a rectangular box where all sides are rectangles.
- Prisms: Visualize a book standing upright, with the same cross-section throughout its height.
- Pyramids: Imagine the Great Pyramid of Giza, with a square base and four triangular faces sloping to an apex.
Non-Polyhedral 3D Shapes
- 3D shapes that are not polyhedra include cylinders, cones, and spheres.
Geometric Shapes: Cylinders, Cones, Spheres
- Cylinders
- Cones
- Spheres
Examples
Image gallerySkip image gallery- Image caption: A 3D shape with regular polygonal faces, meeting at equal angles, is a platonic solid. There are five platonic solids: the tetrahedron, cube, octahedron, dodecahedron, and icosahedron.

- Image caption: The tetrahedron, octahedron, and icosahedron have faces that are all equilateral triangles. Tetra means four. A tetrahedron has four faces, with three triangles meeting at each vertex. Octa means eight. An octahedron has eight faces with four triangles meeting at each vertex. Icosa means twenty. An icosahedron has 20 faces with five triangles meeting at each vertex.
- Image caption: A cube has six square faces, with three squares meeting at each vertex. A dodecahedron has 12 pentagonal faces, with three pentagons meeting at each vertex.
3D Shapes and Their Characteristics
- 3D shapes with flat polygon faces, straight edges, and sharp vertices are diverse, including cuboids, prisms, and pyramids.
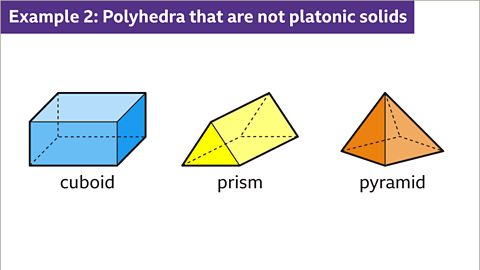
- A cuboid possesses six rectangular faces, where opposite faces are congruent.
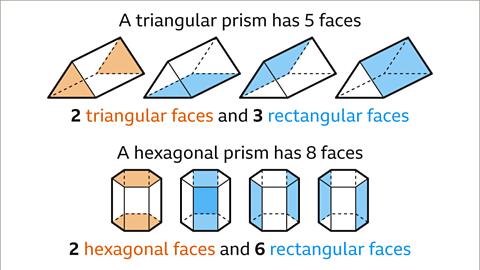
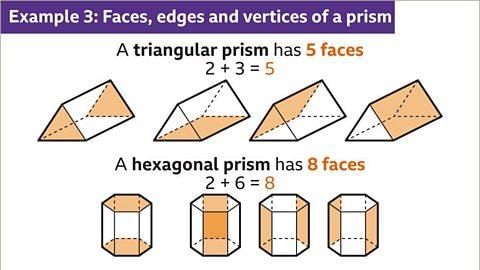
- A prism represents a 3D figure with a constant polygon-shaped cross-section. The name of a prism is derived from the shape of its polygon cross-section. For instance, a triangular prism features a triangular cross-section, while a hexagonal prism showcases a hexagonal one.
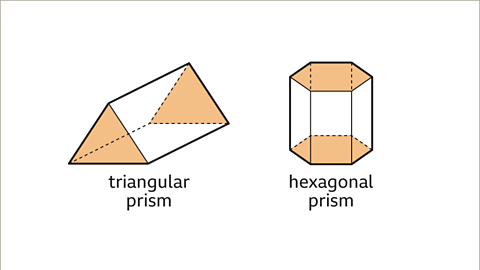
- Each prism consists of congruent polygon 'ends' along with the rectangles that connect them. The number of rectangular faces in a prism corresponds to the sides of its polygon cross-section. For instance, a triangular prism boasts three rectangular faces and two triangular faces, totaling five surfaces. On the other hand, a hexagonal prism contains six rectangular faces and two hexagonal faces, summing up to eight faces.
Pyramids
- A pyramid consists of a polygonal base face and triangular faces meeting at a point called the apex. The naming convention of a pyramid is based on the shape of its base.
- A triangle-based pyramid is a pyramid with a triangular base, while a square-based pyramid has a square base.
- A tetrahedron is a triangular pyramid with all equilateral triangle faces.
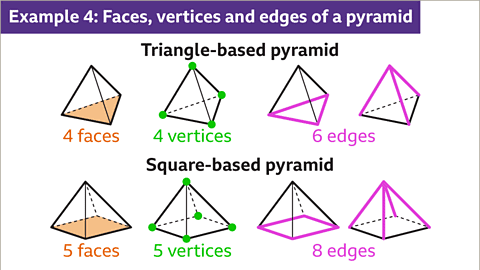
Triangle-based Pyramid
 Image caption: A pyramid is made up of a polygonal base face and triangular faces that meet at a point called the apex. A pyramid is named by the shape of its 'base'. A pyramid with a triangular base is a triangle-based pyramid. A tetrahedron is a triangular pyramid with all equilateral triangle faces. A pyramid with a square base is a square-based pyramid.
Image caption: A pyramid is made up of a polygonal base face and triangular faces that meet at a point called the apex. A pyramid is named by the shape of its 'base'. A pyramid with a triangular base is a triangle-based pyramid. A tetrahedron is a triangular pyramid with all equilateral triangle faces. A pyramid with a square base is a square-based pyramid.Square-based Pyramid
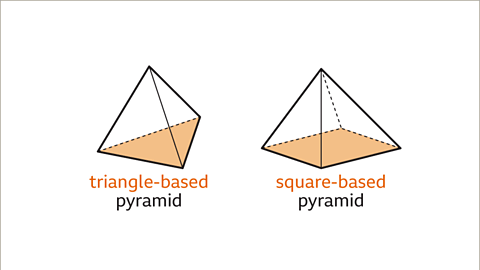 Image caption: A pyramid is made up of a polygonal base face and triangular faces that meet at a point called the apex. A pyramid is named by the shape of its 'base'. A pyramid with a triangular base is a triangle-based pyramid. A tetrahedron is a triangular pyramid with all equilateral triangle faces. A pyramid with a square base is a square-based pyramid.
Image caption: A pyramid is made up of a polygonal base face and triangular faces that meet at a point called the apex. A pyramid is named by the shape of its 'base'. A pyramid with a triangular base is a triangle-based pyramid. A tetrahedron is a triangular pyramid with all equilateral triangle faces. A pyramid with a square base is a square-based pyramid.Non-Polyhedral 3D Shapes
- Non-polyhedral 3D shapes include cylinders, cones, and spheres, where at least one face is not a polygon.
- A cylinder has a constant circular cross-section, two circular faces, and one curved rectangular face.
- A cone features a circular base and one curved face made from a sector of a circle.
- A sphere is completely curved, resembling a ball shape.
Example of Non-Polyhedral Shapes
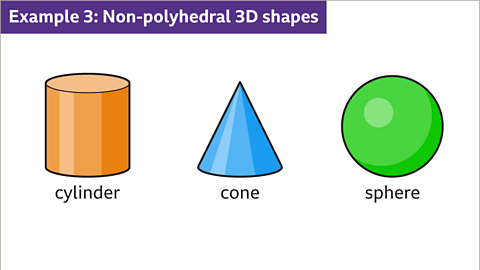 Image caption: 3D shapes that are non-polyhedral include cylinders, cones, and spheres. At least one face is not a polygon. At least one face has a curved surface. A cylinder has a constant circular cross-section, two circular faces and one curved rectangular face. A cone has a circular base and one curved face made from a sector of a circle. A sphere is completely curved, a ball shape.
Image caption: 3D shapes that are non-polyhedral include cylinders, cones, and spheres. At least one face is not a polygon. At least one face has a curved surface. A cylinder has a constant circular cross-section, two circular faces and one curved rectangular face. A cone has a circular base and one curved face made from a sector of a circle. A sphere is completely curved, a ball shape.
Shapes in 3D Geometry
- Image caption: A cylinder has a constant circular cross-section, two circular faces, and one curved rectangular face. A cone has a circular base and one curved face made from a sector of a circle. A sphere is completely curved, resembling a ball shape.
- Image:

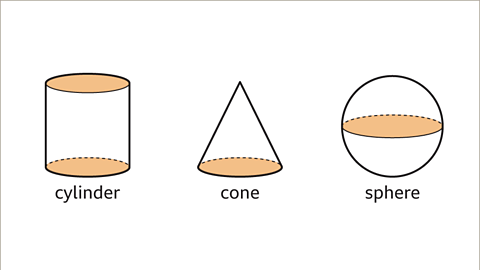
Basic 3D Shapes
- A cylinder features a circular cross-section and two circular faces along with a curved rectangular face.
- A cone includes a circular base and a single curved face formed from a sector of a circle.
- A sphere is entirely curved, resembling a ball shape.
Platonic Solids
- Slide 1 of 10 - Example one: The Platonic Solids
- A series of five images showcasing regular three-dimensional shapes:
- A yellow tetrahedron, a blue cube, an orange octahedron, a green dodecahedron, and a pink icosahedron.
- Each of these shapes is a Platonic solid, characterized by regular polygonal faces meeting at equal angles.
- There are five Platonic solids: the tetrahedron, cube, octahedron, dodecahedron, and icosahedron.
Understanding Vertices, Edges, and Faces of Polyhedra
- Definition of Vertices: Vertices are points where two or more edges meet in a shape. They are essentially the corners of a geometric figure. The plural form of vertex is vertices.
- Example of Vertices: Think of a cube where the points where three edges meet are the vertices.
- Definition of Edges: Edges are the lines that are formed by connecting two vertices in a shape. They are also formed where two faces of a shape meet.
- Example of Edges: In a pyramid, the lines along the sides where two faces meet are the edges.
- Definition of Faces: Faces are the flat surfaces of a three-dimensional solid shape. These surfaces enclose the space inside the shape.
- Example of Faces: In a rectangular prism, each of the six flat surfaces is a face of the prism.
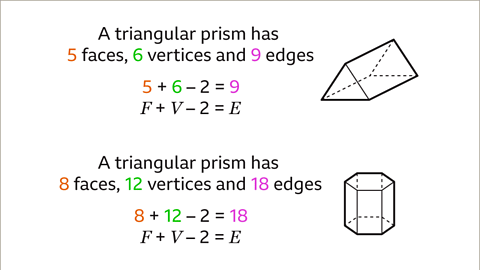
- Relationship among Vertices, Edges, and Faces: In any polyhedron, the number of edges is always two less than the sum of the number of vertices and faces. This relationship is mathematically represented as E = V + F - 2.
- Illustrative Explanation: Consider a tetrahedron with 4 vertices and 4 faces. According to the formula, the number of edges would be 4 (vertices) + 4 (faces) - 2 = 6 edges.
Understanding Geometric Solids
Examples
- Image caption: The flat surface of a cube is a face. Each face of a cube is a square. Two faces are joined by an edge. Three square faces meet at a vertex.
- Image caption: A cube has six faces, eight vertices, and twelve edges.
- Image caption: For any 3D shape that is a polyhedron, the number of edges is equal to two less than the sum of the vertices and faces. This is the formula E = F + V - 2.
- Image caption: For a cube, E = 12, F = 6, and V = 8. The number of edges can be calculated by adding the number of faces and vertices and subtracting two. F + V - 2 = E. 6 + 8 - 2 = 12.
- Image caption: A prism has two end faces that match the cross-section, plus a rectangular face for each side of the end face. A triangle has three sides. A triangular prism has five faces, the two triangles for each end plus three rectangular faces that join them. A hexagonal prism has eight faces, the two hexagons for each end plus six rectangular faces that join them.
Image Gallery
Examples are visually represented through the following images:
 |
 |
 |
Conclusion
Understanding the basic concepts of geometric solids is crucial for further mathematical explorations. By grasping the relationships between faces, vertices, and edges, one can delve deeper into the fascinating world of 3D shapes.
Understanding Prism Geometry
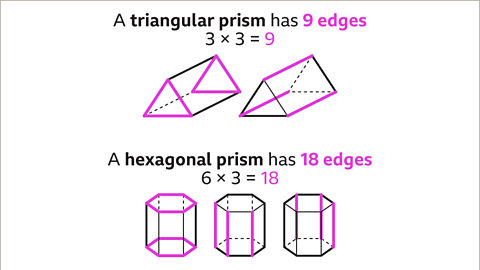
Edges of a Prism
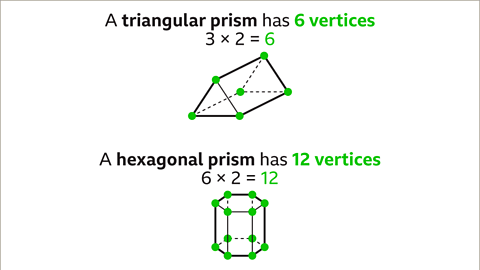
The number of edges of a prism is determined by the number of edges of its end face, multiplied by three. For instance, in a triangular prism, each end face has three edges, and there are three additional edges joining them together. Therefore, a triangular prism has a total of 9 edges (3 x 3 = 9). Similarly, a hexagonal prism, with six edges for each end face and six additional edges joining them, totals to 18 edges (6 x 3 = 18).Vertices of a Prism
The vertices of a prism are located at each end of the 3D shape. The count of vertices is twice the number of vertices of an end face. In a triangular prism with two triangular faces, the total vertices amount to 6 (3 x 2 = 6). Similarly, a hexagonal prism, featuring two hexagonal end faces, has a total of 12 vertices (6 x 2 = 12).- Prisms are a type of polyhedron with specific characteristics:
- A triangular prism has 5 faces, 6 vertices, and 9 edges.
- A hexagonal prism has 8 faces, 12 vertices, and 18 edges.
- Pyramids have unique features based on their base shapes:
- A triangle-based pyramid has 4 faces, 4 vertices, and 6 edges.
- A square-based pyramid has 5 faces, 5 vertices, and 8 edges.
- Pyramids are a type of polyhedron, and a specific formula, 𝑉 = 𝐹 - 𝐸, applies to them.
- For a triangle-based pyramid, with 4 faces and 4 vertices, the formula gives 6. (4 * 4) - 2 = 6.
- Similarly, for a square-based pyramid, with 5 faces and 5 vertices, the formula yields 8. (5 * 5) - 2 = 8.
- Triangle-based pyramid: 4 faces + 4 vertices - 2 = 6 edges.
- Square-based pyramid: 5 faces + 5 vertices - 2 = 8 edges.
- A cube consists of faces, edges, and vertices, each with distinct properties.
- Face: The flat surface of a cube, forming a square.
- Edge: Where two faces of a cube meet.
- Vertex: Where three edges meet in a cube.
- Images illustrating cube components: face, edge, and vertex, each highlighted for clarity.
- Understanding the geometric properties of pyramids and cubes is crucial in geometry, offering insights into their structural composition.
- Platonic solid: A polyhedron with regular polygon faces such as the tetrahedron, cube, octahedron, dodecahedron, and icosahedron, used to make dice.
- One key property of a platonic solid is that all its faces are identical (congruent). This characteristic ensures that the chance of landing on each face is equally likely, making the dice fair.
- The most common type of platonic solid dice is the 6-sided cube dice, although various other shapes are utilized in role-playing games.
- The main aim of Divided Islands is to expand your territory while strategically defending it from opponents.
- Players start with a set number of territories and resources.
- Each turn allows players to either expand their territory or reinforce their defenses.
- Strategic decisions include where to attack, where to defend, and how to manage resources efficiently.
- Focus on securing key strategic locations early in the game to establish a strong foothold.
- Use diplomacy to form alliances with other players for mutual benefit.
- Adapt your strategy based on the actions of opponents to stay ahead in the game.
- Winning the game requires either complete domination of the map or achieving specific objectives outlined at the beginning.
- Players must balance offense and defense to succeed in Divided Islands.
Prisms and Pyramids in Geometry
Prisms and pyramids are fundamental geometric shapes with distinct properties.
Prisms
Pyramids
Illustrative Examples
 |  |
These shapes play a crucial role in geometry, offering insights into spatial relationships and mathematical concepts.
Pyramids and Polyhedrons
Illustrative Examples
Cube Characteristics
Characteristics Explained
Visual Representation
Conclusion
| Slide Number | Content |
|---|---|
| 1 of 10 | Example one: Images depicting cube components and their relationships, aiding in visual comprehension. |
Questions
Back to topPractise working out properties of 3D shapes
Practise working out properties of 3D shapes with this quiz. You may need a pen and paper to help you with your answers.
Quiz
Back to topReal-life maths
 Image caption
Image caption Game - Divided Islands
Divided Islands is a strategic game that challenges players to conquer and defend territories on a map divided into distinct sections.
Objective of the Game
Gameplay Overview
Key Strategies
Victory Conditions
| Player | Territories | Resources |
|---|---|---|
| Player 1 | 12 | 50 |
| Player 2 | 10 | 45 |
| Player 3 | 15 | 55 |
 Image caption, Back to top
Image caption, Back to top 


















