Converting metric units for area and volume - Year 7 PDF Download

Key points

• Area and Volume Measurement:
  • Area is a measure of the size of a surface or 2D shape, typically in square units like square centimeters (cm²) or square meters (m²).
  • Volume represents the space occupied by a 3D shape, measured in cubic units such as cubic centimeters (cm³) or cubic meters (m³).
  • Both area and volume are commonly measured in metric units for consistency.
  • It is crucial to use the same units when comparing or combining areas or volumes to avoid misconceptions.
• Common Misconception:
  • Incorrectly assuming that the conversion between lengths is the same as the conversion between areas or volumes.
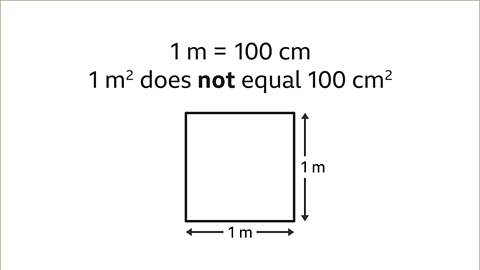
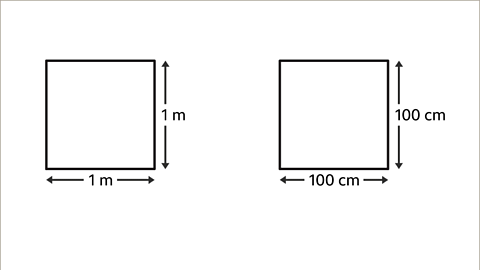
  • For example, 1 meter is equivalent to 100 centimeters, but 1 square meter is not the same as 100 square centimeters.

Geometric Concepts

• Area: Area is a measure of the size of any 2D shape or plane surface. It is quantified in square units such as cm² or m². For instance, when we calculate the area of a rectangle, we multiply its length by its width to determine the space it covers on a flat surface.
• Volume: Volume represents the amount of space occupied by a 3D shape. It is measured in cubic units like cm³, mm³, or m³. For example, when we calculate the volume of a cube, we multiply its length by its width by its height to ascertain the space it occupies in three dimensions.
• When comparing or combining areas or volumes, it is crucial to utilize the same units of measurement. Failure to convert the measurements into a uniform unit can lead to confusion. For instance, comparing 400cm² with 4m² directly may be misleading without converting one of them into the other unit for a fair assessment.

Common Misconceptions in Measurement Conversions

A misconception arises when incorrect thinking leads to misunderstandings in measurement conversions.

• A common misconception is assuming that the conversion ratio for lengths applies to areas. For instance, while 1 meter equals 100 centimeters, 1 square meter is not equivalent to 100 square centimeters.

Explanation with Examples

Let's delve deeper into this misconception with examples:

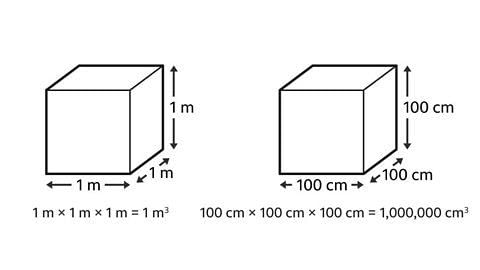
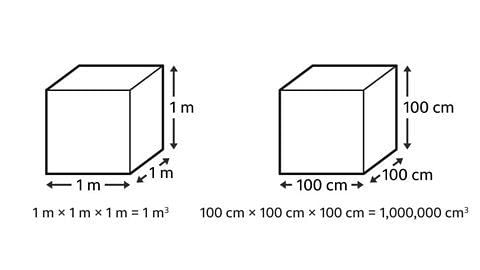
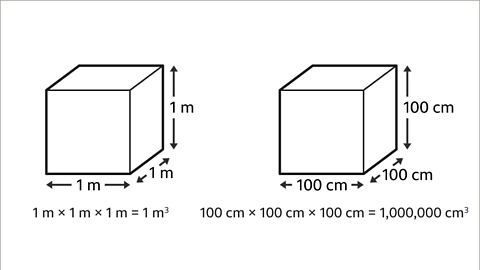
• Consider a cube where each side is labeled as 1 meter. The volume of this cube is 1 cubic meter (1m³).
• Now, envision another cube with each side labeled as 100 centimeters. The volume of this cube is 1 million cubic centimeters (1,000,000 cm³).

Visual Representation

Refer to the images below for a visual representation:

Conclusion

It is crucial to differentiate between linear and square units when converting measurements to avoid common misconceptions.

Back to top

Converting units for area

• Objects can be measured in various units based on their size, highlighting the significance of understanding conversions within metric units.
• The process of converting units for area, which represents the size of any flat surface or 2D shape, involves measurements in square units like square centimeters (cm²) or square meters (m²). This method mirrors the process of converting length units, emphasizing that an area encompasses two dimensions - such as length and width.
• During conversions, it's vital to grasp how many smaller units are necessary to compose a larger unit.

Concepts in Geometry

• Area: Area is a measure of the size of any flat surface or 2D shape. It is quantified in square units such as square centimeters (cm²) or square meters (m²).
• Dimension: Dimension refers to the length, width, height, or depth of an object.

Understanding Unit Conversion

• When converting one type of unit to another, it is essential to determine how many smaller units are required to form one larger unit.

Examples:

• Calculating the area of a rectangular room involves multiplying its length by its width in meters (m²).
• For instance, to convert 1 meter (m) to centimeters (cm), you multiply by 100 (1m = 100cm).

Image 1	Image 2

Examples

• Image caption: Calculate the area in square centimeters needed to cover a 1 square meter area.

• Image caption: Clarification on the misconception that 100 cm² are needed for a 1 m² area.

• Image caption: Importance of understanding dimensions when converting units for area calculations.

• Image caption: Calculating areas in square meters and square centimeters for comparison.

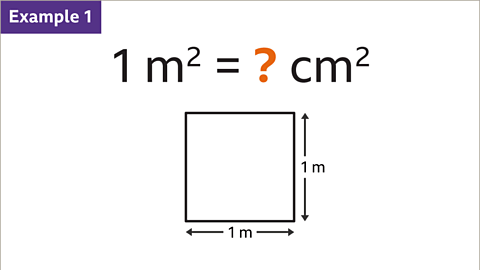
Summary

• Calculating the area in square centimeters for a 1 square meter area is essential and not as straightforward as it might seem.
• Many mistakenly believe that 100 cm² are needed for a 1 m² area, which is incorrect due to dimensional differences.
• Understanding the dimensions and units conversion is crucial when dealing with area calculations, especially with squares.
• Comparing the areas of squares labeled in meters and centimeters highlights the significant difference in the calculated values.

Understanding Area Conversion

Here is a detailed explanation of how to convert areas between different units:

Converting Between Units

• When converting between units for an area calculation, ensure to convert both dimensions (length and width) to the required unit before finding the area.
• Calculate the area conversion factor based on the units being converted.
• For conversions from a larger unit to a smaller unit (e.g., m² to cm²), multiply the conversion factor.
• For conversions from a smaller unit to a larger unit (e.g., mm² to cm²), divide using the conversion factor.

Example Calculation

• Convert 60,000 cm² into m²:
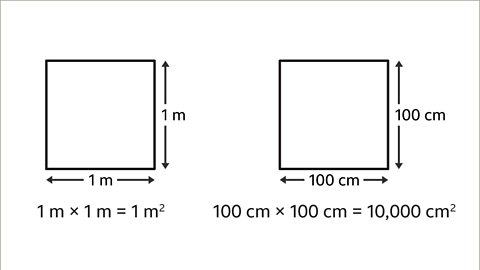
  • 1 m = 100 cm
  • 1 m² = 100 cm x 100 cm = 10,000 cm²
  • Conversion factor is 10,000
• The smaller unit (cm²) is converted to a larger unit (m²) by dividing:
  • 60,000 cm² = 60,000 ÷ 10,000 = 6 m²

Understanding Conversion Factors

• Conversion factors are crucial in converting areas between different units.
• They help in determining the relationship between the units and facilitate accurate conversions.

Key Takeaways

• Always convert dimensions to the same unit before calculating area.
• Remember to use the appropriate conversion factor based on the units being converted.

Original Image	Conversion Process

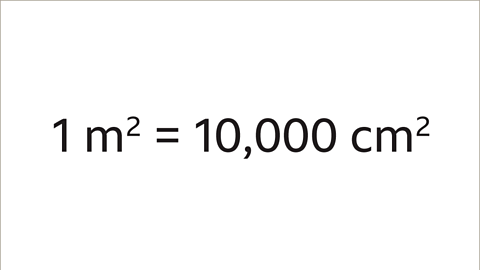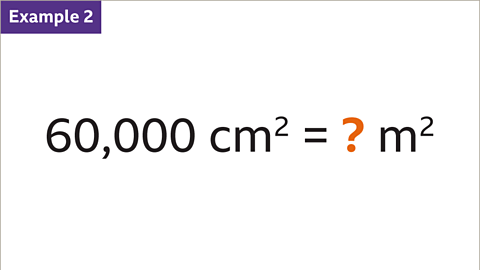Conversion of Area Units

• Converting cm² to mm²: To convert 20 cm² into mm², we know that 1 cm = 10 mm. Therefore, 1 cm² equals 100 mm². Hence, 20 cm² equals 20 x 100 = 2000 mm².

Illustrative Examples

• Example 1: Consider a square with sides labeled as one meter. If we need to find out how many cm² are required to cover an area of 1 m², we can apply the conversion. One meter squared equals a question mark cm², which is 100 x 100 cm².

Question

Back to top

Converting units for volume

• Objects come in various sizes and can be measured using different units. Understanding conversions between metric units is crucial.
• The process of converting units for volume involves determining the space occupied by a 3D object, typically measured in cubic units like cm³, mm³, and m³. Volume is also known as capacity.
• Converting volume units is akin to converting length units, but it's essential to note that volume incorporates three dimensions - length, width, and height.
• When converting from one unit to another, it's important to ascertain how many smaller units are necessary to make up one larger unit.

Volume and Dimension

• Volume: The volume is the amount of space occupied by a 3D shape, measured in cubic units such as cm³, mm³, and m³. It can also be referred to as capacity.
• Dimension: Dimension refers to the length, width, height, or depth of an object.

Conversion of Units

• When converting one type of unit to another, it is essential to understand how many smaller units are required to form one larger unit.

Understanding Volume Conversion

• When we consider volume and conversion of units, it's crucial to grasp the relationship between different units of measurement.
• Visualizing this concept can help us comprehend how dimensions alter when we convert between units.

Examples

• Calculating Volume Equivalents
• Common Misconceptions in Volume Conversion
• Important Points to Remember

Calculating Volume Equivalents

• Given a cube of 1 meter by 1 meter by 1 meter, the volume is 1 cubic meter (1 m³).
• For the same cube in centimeters (100 cm by 100 cm by 100 cm), the volume is 1,000,000 cubic centimeters (1,000,000 cm³).

Common Misconceptions in Volume Conversion

• Mistakenly assuming that 1 meter cubed is equal to 100 centimeters cubed due to the 1:100 relationship between meters and centimeters.

Important Points to Remember

• Volume calculations involve three dimensions: length, width, and height.
• When converting between units, it's essential to recognize that each dimension changes according to the conversion factor.
• Illustrating this with two cubes, one in meters and the other in centimeters, can aid in visualizing the impact of unit conversion on volume.

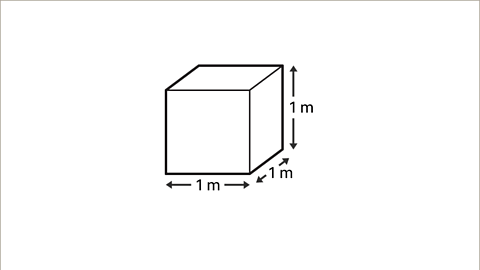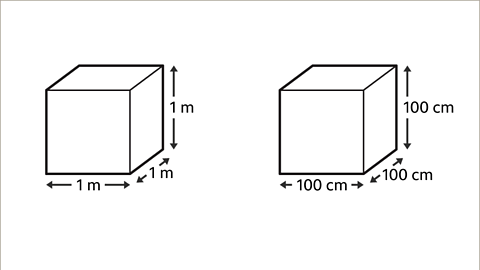Understanding Volume Conversion

• When converting between units for volume calculations, it's essential to convert all three dimensions (length, width, and height) to the required unit before determining the volume. This involves calculating the volume conversion factor.
• For converting from a larger unit to a smaller unit (e.g., m³ to cm³), multiplication is used. Conversely, when converting from a smaller unit to a larger unit (e.g., mm³ to cm³), division is employed.

Example:

• To convert 50,000 mm³ into cm³, given that 1 cm = 10 mm, we follow the conversion steps. 1 cm³ equals 10 mm × 10 mm × 10 mm, which equals 1000 mm³. The conversion factor in this case is 1000.
• Further, to convert the smaller unit (cm³) to a larger unit (m³), the process involves dividing 50,000 mm³ by 1000, resulting in 50 cm³.

Illustrative Example:

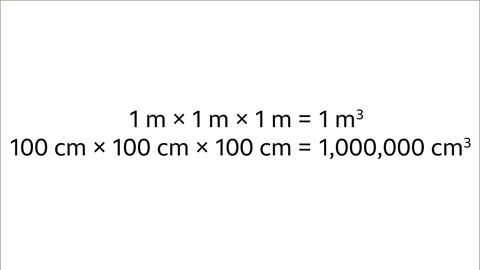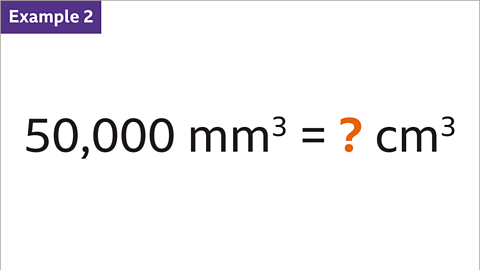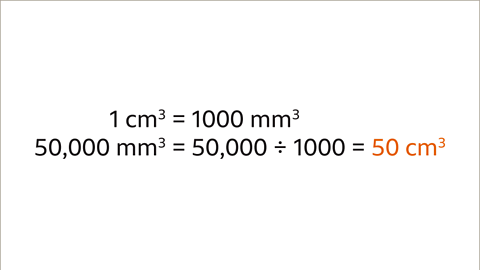Conversion of Cubic Meters to Cubic Centimeters

Worked Examples

Conclusion

Practise working out how to convert metric units for area and volume

Practice calculating metric units for area and volume by engaging in this quiz. Utilize pen and paper to assist with your responses.

Quiz

• Understand Metric Units Conversion: Practice converting metric units for area and volume. For instance, convert square meters to square centimeters.
• Area Conversion Example: Calculate the area of a rectangular field given its length and width in meters.
• Volume Conversion Exercise: Solve problems converting cubic meters to cubic centimeters.

Game - Divided Islands

• Engage in Practical Conversion Scenarios: Participate in a game involving metric unit conversions for real-world applications.
• Interactive Learning: Explore interactive scenarios to reinforce understanding of metric unit conversions.