Intersection of two sets - Year 7 PDF Download
Key points
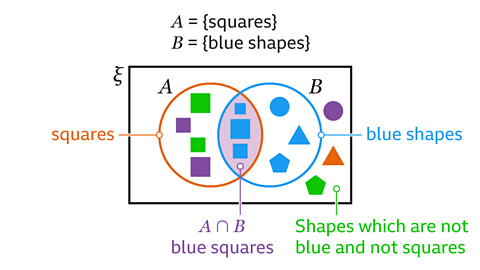 Image caption
Image caption- An element of a set is a piece of information, letter, or number that belongs to the set. It can be represented as a member of that set. For instance, on a Venn diagram, a set is visualized as a circle.
- An element that belongs to two different sets is considered a member of both sets and exists in the intersection of those sets (symbolized as ∩). This intersection on a Venn diagram indicates the area where sets overlap. The intersection of set A and set B, denoted as A ∩ B, includes elements common to both sets.
- The concept of the highest common factor (HCF) relates to finding the largest factor that divides into multiple numbers. This can be determined using the intersection of sets on a Venn diagram, which serves as a tool for organizing data.
Element and Set Theory
A set is a collection of information, letters, or numbers. The set is typically denoted by curly brackets { }.
- An element is a piece of information, a letter, or a number that belongs to a set as a member.
Intersection of Sets
When an element is present in two different sets, it is considered part of the intersection of those sets, denoted by ∩.
- An element in the intersection of two sets belongs to both sets. For example:
- If set A = {1, 2, 3} and set B = {2, 3, 4}, then A ∩ B = {2, 3}.
| Venn Diagram |
|---|
 |
Understanding Sets and Venn Diagrams
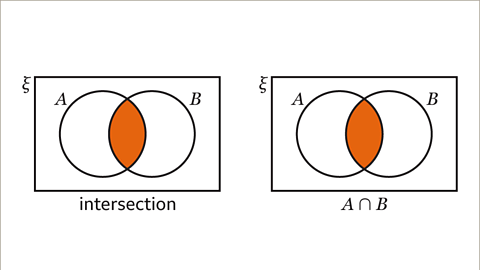
- Intersection (of sets): On a Venn diagram, this refers to the area where sets overlap. It represents elements that are common to both sets. For instance, if we have set A and set B, then A ∩ B = {elements in A that are also in B}.
Key Concepts:
- The intersection of sets includes elements that are shared among all the sets under consideration.
Application in Mathematics:
- Highest Common Factor (HCF): This is the largest factor that can divide into two or more numbers. For example, the HCF of 30 and 20 is 10. It is denoted as HCF. In Venn diagrams, the concept of intersections is used to find the HCF.
Example:
- Consider two sets: Set X = {2, 4, 6, 8} and Set Y = {4, 6, 8, 10}. The intersection of X and Y, denoted as X ∩ Y, would be {4, 6, 8} since these elements are common to both sets.
Highest Common Factor (HCF)
- The highest common factor (HCF) is the largest factor that will divide into the selected numbers.
- For example, 10 is the highest common factor of 30 and 20. The HCF is denoted as "HCF."
Venn Diagram
- A Venn diagram is a graphical representation used to organize and categorize data.
- It visually demonstrates relationships between different sets of data.
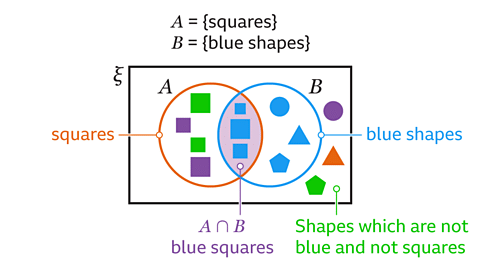 Image captionBack to top
Image captionBack to topUnderstanding and Using the Intersection of Sets
- The intersection of two or more sets represents the common elements shared by those sets.
- The symbol ∩ is employed to indicate the intersection of sets where they overlap or coincide.
- The intersection of sets A and B, denoted as A ∩ B, comprises elements that are present in both A and B.
- Similarly, A ∩ B ∩ C signifies the intersection of sets A, B, and C, containing elements common to all three sets.
- To denote the complement of a set, the symbol ' is appended after the set name. For instance, Q' denotes the complement of set Q.
Set Theory Concepts
- The intersection of sets A, B, and C (A∩B∩C) is the set of elements that are common to all three sets.
- The complement of a set is denoted by adding a prime symbol ('), such as Q' for the complement of set Q.
Examples
Image gallerySkip image gallery- Image caption: The intersection of a set represents the overlap between the sets. 𝕨∩𝕩 is the intersection of set 𝕨 and set 𝕩.
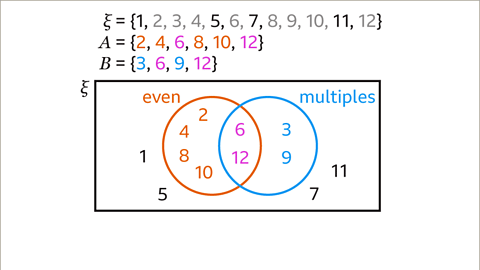
- Image caption: Draw the Venn diagram where ξ = {whole numbers from 1 to 12 inclusive}, 𝕨 = {even numbers}, and 𝕩 = {multiples of three}. List the elements of 𝕨∩𝕩 and describe the intersection.
- Image caption: List the elements of each set.


Understanding Venn Diagrams
Here is a detailed explanation of Venn diagrams with examples and explanations:
Set Intersection in Venn Diagrams
Place the elements that are common to sets 6 and 12 in the intersection. Complete set A with 2, 4, 8, and 10. Complete set B with 3 and 9. Complete the universal set with 1, 5, 7, and 11.Multiples and Even Numbers
The intersection of even numbers and multiples of 3 gives the set of multiples of 6. This can be represented as: A ∩ B = {multiples of 6}.Shapes with Line and Rotational Symmetry
The Venn diagram illustrates shapes with line symmetry and shapes with rotational symmetry. The intersection of these sets shows shapes with both line and rotational symmetry.
| Image | Description |
|---|---|
 | Explanation of Set Intersection |
 | Illustration of Multiples and Even Numbers |
 | Explanation of Shapes with Symmetry |
Understanding Venn Diagram Intersections
Venn diagrams are powerful tools used to visualize relationships between different sets. When sets intersect, it signifies elements shared between them. Let's delve into the key concepts and examples:
The Intersection of Two Sets
The intersection of a set refers to the common elements shared between them. For instance, A ∩ B represents the elements present in both set A and set B.
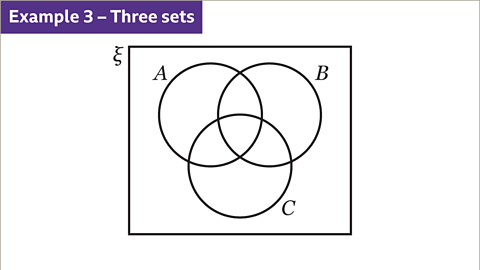
The Intersection of Three Sets
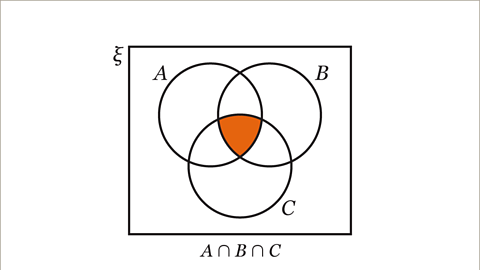
When we talk about A ∩ B ∩ C, we are referring to elements that are common to all three sets: A, B, and C. This illustrates the shared elements across all sets.
Question
Back to top
 |
Download the notes
Intersection of two sets
|
Download as PDF |
Use a Venn diagram to find the HCF of two or more numbers
- To use a Venn diagram to find the HCF (highest common factor) of two or more numbers:
Understanding Highest Common Factor (HCF) through Prime Factorization
Calculating HCF of Numbers
In order to find the Highest Common Factor (HCF) of two numbers, you need to break down each number into its prime factors.
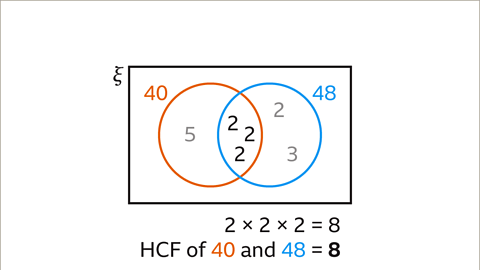
- Example: Find the HCF of 40 and 48
- Prime factorization of 40: 2 × 2 × 2 × 5
- Prime factorization of 48: 2 × 2 × 2 × 2 × 3
Visual Representation with Venn Diagram
Representing prime factors of numbers through a Venn diagram can simplify the concept.
- Draw one circle each for 40 and 48
- Common prime factors go in the intersection, while unique prime factors go in respective circles
- For 40 and 48, the common prime factors are three 2s
- Inside the circle for 40: 5 (unique factor)
- Inside the circle for 48: 2 and 3 (unique factors)
Understanding Highest Common Factor (HCF)
- When finding the Highest Common Factor (HCF) of two numbers, such as 40 and 48, we look for the greatest number that divides both numbers evenly.
- The HCF is determined by identifying the common prime factors of the given numbers.
- In the case of 40 and 48, the common factors are 2 × 2 × 2, which equals 8.
- Therefore, the HCF of 40 and 48 is 8.
Illustrative Example
- In a Venn diagram representing the numbers 40 and 48, the intersection contains three 2s, which are the common factors.
- These common factors, 2 × 2 × 2, constitute the HCF calculation method.
- The HCF, being 8, is the highest number that can divide both 40 and 48 without leaving a remainder.
Question
Consider the Venn diagram below. How would you find the HCF of 40 and 48 based on the common factors?
 |  |
Practise understanding and using the intersection of two sets
Quiz
Game - Divided Islands
Back to top- Understand the concept of set intersection
- Identify common elements in two sets
- Apply intersection operation symbolically (A ∩ B)
- Explain with an example: Set A = {1, 2, 3}, Set B = {3, 4, 5}
- Determine the intersection: A ∩ B = {3}

















