Olympiad Notes: Algebra | Maths Olympiad Class 6 PDF Download
Introduction
- Algebra is a branch of mathematics, which involves using letters and symbols to represent numbers in equations.
- It's particularly useful for solving problems involving unknown quantities.
- Algebra provides a structured approach to tackling mathematical puzzles with variables.
Matchstick Patterns

- No. of matchsticks used to make 1st square = 4.
- No. of matchsticks used to make 2nd square = 7.
- No. of matchsticks used to make 3rd square = 10.
- So, the pattern that we observe here is 3n + 1.
With this pattern, we can easily find the number of matchsticks required in any number of squares.
Example: Find the number of matchsticks that will be used in pattern 32.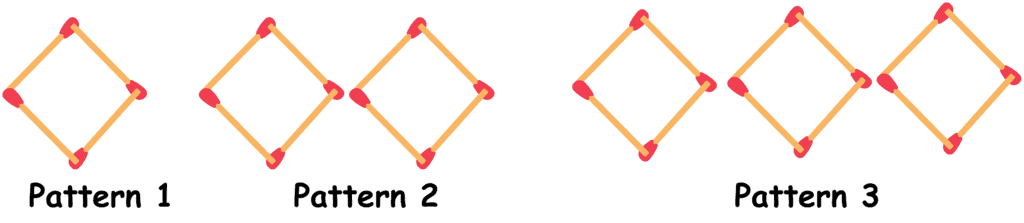
Sol: No. of matchsticks used in 1st Pattern = 4
No. of matchsticks used in 2nd Pattern = 8
No. of matchsticks used in 3rd Pattern = 12
So, the pattern we observe here is = 4n, (n = 1, 2, 3, 4, ...)
Hence, no. of matchsticks that will be used in 32nd Pattern = 4 x 32 = 128
Variable
- A variable is a quantity whose value can vary depending on the situation.
- It represents an unknown value that can change.
- For instance, in the expression 2x+5, the letter x is the variable.
Constant
- A quantity whose value does not vary is called a constant.
- For instance, in the expression 2x+5, 5 is a constant.
Expressions
- Arithmetic expressions involve numbers and basic math operations like adding, subtracting, multiplying, and dividing.
- They're like the building blocks of math, helping us solve problems and make sense of numbers in real life.
Example: 2 + (9 – 3), (4 × 6) – 8
(4 × 6) – 8 = 24 – 8
= 16
Expressions with variable
- Expressions in algebra often include variables, such as "2m" or "5 + t."
- These variables represent unknown quantities that can take on different values.
- Until we assign specific values to the variables, we can't fully evaluate or analyze the expression.
Example: Find 3x – 12 if x = 6.
Sol: (3 × 6) – 12
= 18 – 12
= 5
Thus, 3x – 12 = 5.
Formation of Expressions
- Algebraic expressions are combinations of variables (like x or y), constants (numbers), and operators (like + or -).
- They're used to represent mathematical ideas or formulas.
Some examples have been given below:-
Practical use of Expressions
Example: Write down the equation justify the given statement.
'The age of Riya is five more than three times the age of her son, where age of Riya is Q and her son is P.'
Sol: Given that,
Age of Riya's son = P
Age of Riya = Q
According to question, Riya's age (Q) is 5 more than three times the age of her son(P).
- 3 times Riya's son's age = 3 x P = 3P
- 5 more than 3 times Riya's son's age = 5 + 3P
Hence, Riya's age , Q =5 + 3P.
Like and Unlike Terms
Like Terms- Like terms are the terms have the same variables in them.
- For example, 8xy and 3xy are like terms.
These terms share the same variables, which are 'x' and 'y'.
Unlike Terms
- When terms in an expression have different variables, they are called unlike terms.
- For instance, 7xy and -3x are unlike terms.
- This means they don't have the same combination of variables.
Monomial, Binomial, Trinomial and Polynomial Terms
Addition and Subtraction of Algebraic Expressions
Addition and Subtraction of Like Terms
- Sum of two or more like terms is a like term.
- Its numerical coefficient will be equal to the sum of the numerical coefficients of all the like terms.
Example: 8y+7y=?
8y
+7y
_______________
(8+7)y = 15y
_______________
- Difference between two like terms is a like term.
- Its numerical coefficient will be equal to the difference between the numerical coefficients of the two like terms.
Example: 11z−8z=?
11z
−8z
_____________
(1-8)z = 3z
_____________
Addition and Subtraction of Unlike Terms
- For adding or subtracting two or more algebraic expressions, like terms of both the expressions are grouped together and unlike terms are retained as it is.
Addition of −5x2+12xy and 7x2+xy+7x is shown below:
−5x2+12xy
7x2+xy+7x
______________
2x2+13xy+7x
______________
Subtraction of −5x2+12xy and 7x2+xy+7x is shown below:
−5x2+12xy
−7x2+xy+7x
_____________
12x2+11xy−7x
__________________
Use of Variables in Common Rules (Geometry)
Perimeter of Square
The perimeter of a square = Sum of all sides= 4 × side
= 4s.
Thus, p = 4s.
Here s is variable, so the perimeter changes as the value of side change.
Perimeter of Rectangle
Perimeter of rectangle = 2(length + breadth)= 2 (l + b) or 2l + 2b
Thus, p = 2 × (l + b) or 2l + 2b, where, l and b are variable and the value of perimeter changes with the change in l and b.
Use of Variables in Common Rules (Arithmetic)
Commutativity of Addition
- The commutative property of addition states that changing the order of addends doesn't change the sum.
- For example, 5 + 4 equals 9, and so does 4 + 5.
- This property means that regardless of the order in which numbers are added, the result remains constant.
- Mathematically, it's expressed as: a + b = b + a, where 'a' and 'b' represent different variables.
Example: a = 16 and b = 20
According to commutative property
16 + 20 = 20 + 16
36 = 36
Commutativity of Multiplication
- When we multiply 8 by 2, we get 16, and when we multiply 2 by 8, we also get 16.
- This shows the commutative property of multiplication, where changing the order of the numbers being multiplied doesn't change the result.
- In mathematical terms, it is expressed as a × b = b × a, where 'a' and 'b' represent any different variables.
Example: 18 ×12 = 216, 12 ×18 = 216
Thus, 18 × 12 = 12 × 18
Distributivity of Numbers
- Let's consider an example, 6 × 32
- It is a complex sum but there is an easy way to solve it. It is known as the distributivity of multiplication over the addition of numbers.
6 × (30 + 2)
= 180 + 12
= 192
Thus, 6 × 32 = 192 - A × (b + c) = a × b + a × c. Here, a, b and c are different variables.
Associativity of Addition
- This property states that the result of the numbers added will remain same regardless of their grouping.
(a + b) + c = a + (b + c)
Example: (4 + 2) + 7 = 4 + (2 + 7)
6 + 7 = 4 + 9
13 = 13
Equation
- When we place an equal sign between two expressions, they become an equation.
- Equations are only true for specific values of the variable.
- The equal sign signifies that the expression on the left-hand side (LHS) is equal to the one on the right-hand side (RHS).
- The value of the variable that makes the LHS equal to the RHS is the only solution to that equation.
- For example, 3 + 2x = 13, 5m – 7 = 3, p/6 = 18, all are equations.
- If there is the greater than or less than sign instead of the equal sign then that statement is not an equation.
Some examples which are not an equation are
(i) 23 + 6x > 8
(ii) 6f – 3 < 24
The Solution of an Equation
- The solution to an equation is the value of the variable that makes the equation true.
- To confirm if a specific value is the solution, we compare the left-hand side (LHS) and the right-hand side (RHS) of the equation with that value.
- If the LHS equals the RHS when we substitute the value of the variable, then that value is indeed the solution.
- This process ensures that the equation is satisfied or balanced for the given value of the variable.
Trial and Error Method
To find the solution of the equation, we use the trial and error method.
Example: Find the value of x in the equation 25 – x = 15.
Sol: Here we have to check for some values which we feel can be the solution by putting the value of the variable x and check for LHS = RHS.
Let’s take x = 5
25 – 5 = 15
20 ≠ 15
So x = 5 is not the solution of that equation.
Let’s take x = 10
25 – 10 = 15
15 = 15
Here, LHS = RHS
Hence, x = 10 is the solution of that equation.
Algebra as Patterns
Number Patterns
- If a natural number is denoted by n, then its successor is (n + 1).
Example: Successor of n=10 is n+1=11. - If a natural number is denoted by n, then 2n is an even number and (2n+1) is an odd number.
Example: If n=10, then 2n=20 is an even number and 2n+1=21 is an odd number.
Patterns in Geometry
- Some geometrical figures follow patterns which can be represented by algebraic expressions.
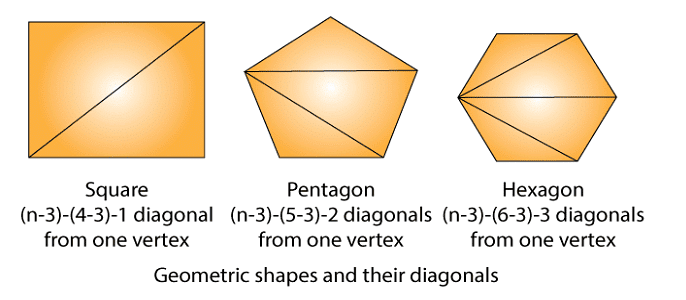
Example: Number of diagonals we can draw from one vertex of a polygon of n sides is (n – 3) which is an algebraic expression.
Practice Questions
Q1: Write the algebraic expression for the statement 'One-fifth of a number x is subtracted from the sum of b and thrice of c'.
Sol: Sum of b and thrice of c = b + 3c.
One - fifth of x = 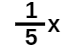
Required expression: b + 3c - 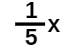 .
.
Q2: Find the value of m in the given equation.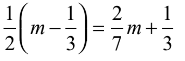
Sol:
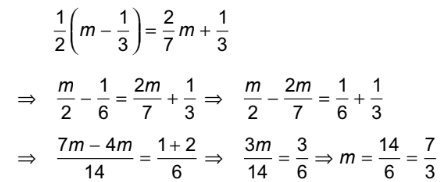
Q3: The present age of Reena is 1/4 of her father’s age. If the present age of her father is 52 years, then what will be the age of Reena after 7 years? Finally, express the present ages of Reena and her father in ratio form.
Sol: Given that,
Present Age of Reena's Father = 52 years
∴ Present Age of Reena = (1/4) * Father's age
= (1/4) * 52
= 13 years
Reena's age after 7 years = Reena's present age + 7
= 13 + 7
= 20 years
Q4: The ratio of the present age of Sonam and Priya be 10 : 9. If sum of their ages be 57 years, then find their present ages respectively
Sol: Let's denote the present age of Sonam as 10𝑥.
And the present age of Priya as 9x, where x is a common multiplier.
A common multiplier is a number that can be multiplied by each term in a ratio or equation to produce equivalent ratios or equations.
In this context, the common multiplier refers to a number that can be multiplied by both parts of the ratio (in this case, the ages of Sonam and Priya) to maintain the same ratio relationship between them.
According to question,
10x+9x=57
19x=57 (Combining like terms)
Now, solve for x:
x = 57/19
x = 3
Now that we have found the value of 𝑥, we can find their present ages:
Sonam's age: 10x=10×3=30 years
Priya's age: 9x=9×3=27 years
So, Sonam's present age is 30 years, and Priya's present age is 27 years.
Q5: The breadth of a rectangular bed sheet is 5 m more than half the length of the bed sheet. What is the perimeter of the bed sheet, if the
length is x m?
Sol:
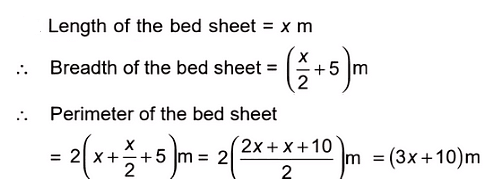
|
8 videos|98 docs|60 tests
|
FAQs on Olympiad Notes: Algebra - Maths Olympiad Class 6
| 1. What are some common algebraic expressions used in geometry? |  |
| 2. How are variables used in common rules in arithmetic? |  |
| 3. How do you differentiate between like and unlike terms in algebraic expressions? |  |
| 4. How do you add and subtract algebraic expressions? |  |
| 5. What are some examples of matchstick patterns in algebra? |  |