IGCSE Class 10 > Class 10 Notes > Mathematics for GCSE/ > Exponential Growth & Decay
Exponential Growth & Decay
Exponential Growth & Decay
The concepts of compound interest and depreciation can be extended to other non-monetary scenarios, such as growing or declining populations.
What is exponential growth?
- When a quantity grows exponentially it is increasing from an original amount, P, by r % each year for n years
- Some questions use a different timescale, such as each day, or each minute
- Real-life examples of exponential growth include population increases, bacterial growth and the number of people infected by a virus
- The same formula from compound interest is used
- Final amount of the quantity is
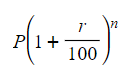
- Substitute values of P, r and n from the question into the formula to find the final amount
- Final amount of the quantity is
What is exponential decay?
- When a quantity exponentially decays it is decreasing from an original amount, P, by r % each year for n years
- Some questions use a different timescale, such as each day, or each minute
- Real-life examples of exponential decay include the temperature of hot water cooling down, the value of a car decreasing over time and radioactive decay (how radioactive a substance is over time)
- The same formula from compound interest is used, but with +r replaced by -r
- Final amount of the quantity is
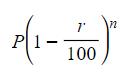
- Substitute values of P, r and n from the question into the formula to find the final amount
- Final amount of the quantity is
How do I use the exponential growth & decay formula?
- To find a final amount, substitute the values of P, r and n (from the question) into the formula
- If the final amount is given in the question, F, set the whole formula equal to this final amount
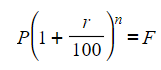
- Some questions then ask to find P, r or n
- To find P or r, rearrange the formula to make P or r the subject (for r, one of the steps involves taking an nth root)
- To find n, use trial and improvement (test different whole-number values for n until both sides of the equation balance)
The document Exponential Growth & Decay is a part of the Class 10 Course Mathematics for GCSE/IGCSE.
All you need of Class 10 at this link: Class 10
FAQs on Exponential Growth & Decay
| 1. What is exponential growth? |  |
Ans. Exponential growth is a process by which a quantity increases at a fixed percentage rate per unit of time. It is characterized by a curved shape on a graph where the rate of increase becomes more rapid over time.
| 2. How is exponential decay different from exponential growth? | |
Ans. Exponential decay is the opposite of exponential growth, where a quantity decreases at a fixed percentage rate per unit of time. This results in a curve on a graph that decreases in a rapid manner over time.
| 3. What are some real-life examples of exponential growth and decay? | |
Ans. Examples of exponential growth include population growth, compound interest in investments, and the spread of viruses. Exponential decay examples include radioactive decay, cooling of a hot object, and depreciation of assets.
| 4. How can we calculate the growth or decay rate in exponential functions? | |
Ans. The growth or decay rate in exponential functions can be calculated using the formula: r = (ln(Nt/N0))/t, where Nt is the final quantity, N0 is the initial quantity, t is the time period, and ln represents the natural logarithm.
| 5. What are some common misconceptions about exponential growth and decay? | |
Ans. One common misconception is that exponential growth or decay will continue indefinitely, which is not always the case as external factors can influence the process. Another misconception is that exponential growth always leads to large numbers quickly, whereas exponential decay always leads to values approaching zero.
About this Document
4.96/5 Rating
Apr 29, 2026 Last updated
Related Exams
Document Description: Exponential Growth & Decay for Class 10 2026 is part of Mathematics for GCSE/IGCSE preparation. The notes and questions for Exponential Growth & Decay have been prepared according to the Class 10 exam syllabus. Information about Exponential Growth & Decay covers topics like and Exponential Growth & Decay Example, for Class 10 2026 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Exponential Growth & Decay.
Introduction of Exponential Growth & Decay in English is available as part of our Mathematics for GCSE/IGCSE for Class 10 & Exponential Growth & Decay in Hindi for Mathematics for GCSE/IGCSE course. Download more important topics related with notes, lectures and mock test series for Class 10 Exam by signing up for free. Class 10: Exponential Growth & Decay
Description
Exponential Growth & Decay of Mathematics covers all the important topics, helping you prepare for the Class 10 exam on EduRev. Start for free!
Information about Exponential Growth & Decay
In this doc you can find the meaning of Exponential Growth & Decay defined & explained in the simplest way possible. Besides explaining types of Exponential Growth & Decay theory, EduRev gives you an ample number of questions to practice Exponential Growth & Decay tests, examples and also practice Class 10 tests
Related Searches
past year papers, Viva Questions, Exponential Growth & Decay, pdf , practice quizzes, Exponential Growth & Decay, shortcuts and tricks, Exam, Objective type Questions, study material, video lectures, MCQs, ppt, Summary, Semester Notes, Exponential Growth & Decay, mock tests for examination, Previous Year Questions with Solutions, Free, Extra Questions, Sample Paper, Important questions;