Notes: Whole Number | Mathematics & Pedagogy Paper 2 for CTET & TET Exams - CTET & State TET PDF Download

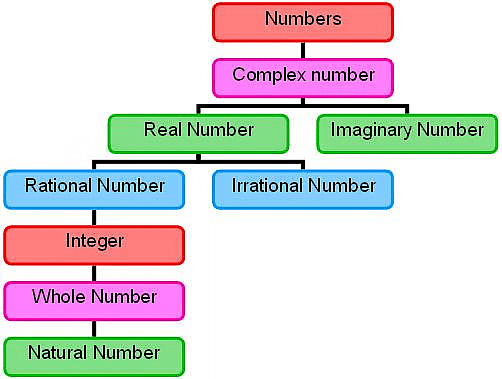
Whole numbers are a fundamental concept in mathematics, encompassing all positive integers (1, 2, 3, ...), zero (0), and their negatives and opposites (-1, -2, -3, ...). These numbers are used to count objects and represent quantities in various contexts, from basic arithmetic to more complex mathematical operations.

In everyday life, whole numbers are used for tasks like counting items in a shopping list, tracking scores in games, and measuring quantities of items. In mathematics, they form the foundation for understanding addition, subtraction, multiplication, and division.

• Whole numbers include natural numbers (that begin from 1 onwards), along with 0.
• Whole numbers are part of real numbers including all the positive integers and zero, but not the fractions, decimals, or negative numbers. 
• Counting numbers are also considered as whole numbers. In this lesson, we will learn whole numbers and related concepts.

Predecessor and Successor

• A successor of any number is the next number to it, which is obtained by adding 1.
• A predecessor of any number is the previous number to it, which is obtained by subtracting 1.
• For example, the predecessor and the successor of the number 12 is 12 – 1 and 12 + 1 which is 11 and 13

Predecessor and Successor

• We see numbers everywhere around the world, for counting objects, for representing or exchanging money, for measuring the temperature, telling time, etc. 
• There is almost nothing that doesn't involve numbers, be it match scores, for players not scoring any run, we say 0 runs, be it cooking recipes, counting on objects, etc.
• Whole Numbers is a set of numbers formed, including all positive integers and 0.
  
  
• Question for Notes: Whole Number

  Try yourself:

  What is a predecessor of a number?

  • A.

    The next number to it, obtained by adding 1.
  • B.

    The previous number to it, obtained by subtracting 1.
  • C.

    A number that is greater than the given number.
  • D.

    A number that is smaller than the given number.

  Explanation

  - A predecessor of a number is the previous number to it.
  - It is obtained by subtracting 1 from the given number.
  - For example, the predecessor of 12 is 12 - 1, which is 11.
  - The predecessor helps us understand the number that comes before a given number in a sequence.
  - It is an important concept in mathematics and is used in various mathematical operations.

  Report a problem

  Cancel Report

  View Solution

What are Whole Numbers?

Natural numbers refer to a set of positive integers and on the other hand, natural numbers along with zero(0) form a set, referred to as whole numbers. However, zero is an undefined identity that represents a null set or no result at all.

• The whole numbers are a set of numbers without fractions, decimals, or even negative integers. It is a collection of positive integers and zero. 
• The symbol to represent whole numbers is the alphabet ‘W’ in capital letters, such as W = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,…
• The primary difference between natural and whole numbers is zero.

Smallest Whole Number

Whole numbers start from 0 (from the definition of whole numbers). Thus, 0 is the smallest whole number.

• The concept of zero was first defined by a Hindu astronomer and mathematician Brahmagupta in 628. 
• In simple language, zero is a number that lies between the positive and negative numbers on a number line. 
• As such zero carries no value, though it is used as a placeholder. So zero is neither a positive number nor a negative number, but it is an even number.

Whole Numbers Vs Natural Numbers

From the above definitions, we can understand that every whole number other than 0 is a natural number.

• Also, every natural number is a whole number. 
• So, the set of natural numbers is a part of the set of whole numbers or a subset of whole numbers.

Set of Whole Numbers

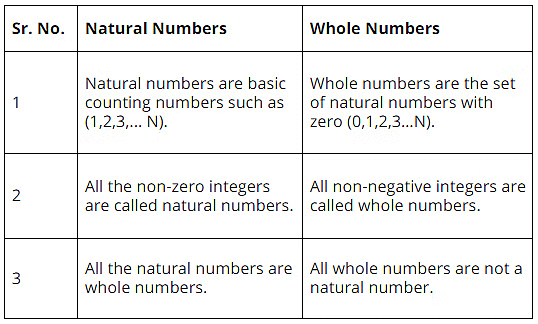
Difference Between Whole Numbers and Natural Numbers

Let's understand the difference between whole numbers and natural numbers through the table given below:

The Number Line

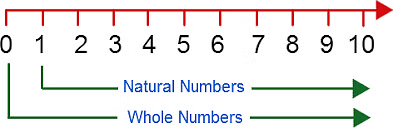
The set of natural numbers and the set of whole numbers can be shown on the number line as given below.

• All the positive integers or the integers on the right-hand side of 0, represent the natural numbers, whereas all the positive integers and zero, altogether represent the whole numbers. 
• Both sets of numbers can be represented on the number line as follows:

What are the Properties of Whole Numbers?

Operations on whole numbers: addition, subtraction, multiplication, and division, lead to four main properties of whole numbers that are listed below:

1. Closure Property
2. Associative Property
3. Commutative Property
4. Distributive Property

Closure Property

• The sum and product of two whole numbers is always a whole number. The closure property of W is stated as follows: For all a,b∈W: a+b∈W and a×b∈W
• Division by Zero
  The division of a whole number by o is not defined, i.e., if x is a whole number then x/0 is not defined.
• Multiplication by Zero
  When a whole number is multiplied to 0, the result is always 0, i.e., x.0 = 0.x = 0.
  
  

Associative Property

• The sum or product of any three whole numbers remains the same though the grouping of numbers is changed.
• The associative property of W is stated as follows: For all a,b,c∈W: a+{b+c}={a+b}+c and a×{b×c}={a×b}×c. For example, 10 + (7 + 12) = (10 + 7) + 12 = (10 + 12) + 7 = 29.

Commutative Property

• The sum and the product of two whole numbers remain the same even after interchanging the order of the numbers. 
• The commutative property of W is stated as follows: For all a,b∈W: a+b=b+a and a×b=b×a. This property states that a change in the order of addition does not change the value of the sum. 
• Let a and b be two whole numbers, commutative property states that a + b = b + a. For example, a = 10 and b = 19 ⇒ 10 + 19 = 29 = 19 + 10. 
• It means that the whole numbers are closed under addition. This property also holds true for multiplication, but not for subtraction or division. For example: 7 x 9 = 63 or 9 x 7 = 63

Distributive Property

• This property states that the multiplication of a whole number is distributed over the sum of the whole numbers. 
• It means that when two numbers, take for example a and b are multiplied with the same number c and are then added, then the sum of a and b can be multiplied by c to get the same answer. 
• This situation can be represented as: a × (b + c) = (a × b) + (a × c). Let a = 10, b = 20 and c = 7 ⇒ 10 × (20 + 7) = 270 and (10 × 20) + (10 × 7) = 200 + 70 = 270. The same is true for subtraction as well. For e.g we have a × (b − c) = (a × b) − (a × c). Let a = 10, b = 20 and c = 7 ⇒ 10 × (20 − 7) = 130 and (10 × 20) − (10 × 7) = 200 − 70 = 130.
• The distributive property of multiplication over addition is a×(b+c)=a×b+a×c. The distributive property of multiplication over subtraction is a×(b-c)=a×b-a×c.

Identity(For Addition and Multiplication)

Additive Identity

When a whole number is added to 0, its value remains unchanged, i.e., if x is a whole number then x + 0 = 0 + x = x

Multiplicative Identity

When a whole number is multiplied by 1, its value remains unchanged, i.e., if x is a whole number then x.1 = x = 1.x

Patterns

Patterns are used for easy verbal calculations and to understand the numbers better.

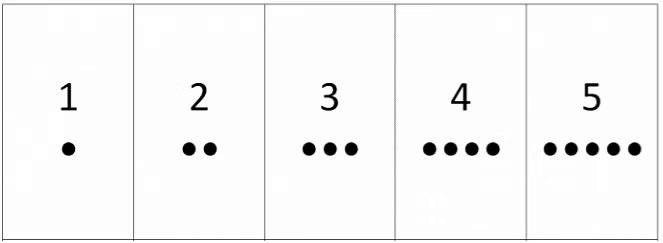
We can arrange the numbers using dots in elementary shapes like triangle, square, rectangle, and lines.

1. We can arrange every number using dots in a line

2. We can arrange some numbers using a rectangle.

Example: 6, 8, 10

3. We can arrange some numbers using a square.

Example: 4, 9, 16

4. We can arrange some numbers using a triangle.

Example: 3, 6, 10, 15, 21

Use of Patterns

Patterns can be used to simplify the process.

1. 123 + 9 = 123 + 10 - 1 = 133 -1 = 132

123 + 99 = 123 + 100 – 1 = 223 – 1 = 222

2. 83 × 9 = 83 × (10-1) = 830 – 83 = 747

83 × 99 = 83 × (100-1) = 8300 – 83 = 8217

[Intext Question]

Important Points

• 0 is a whole number but it is NOT a natural number.
• Negative numbers, fractions, and decimals are neither natural numbers nor whole numbers unless they can be simplified as a natural number or whole number.
• W is closed, associative, and commutative under both addition and multiplication (but not under subtraction and division).

Questions For You

Q.1. Write three consecutive whole numbers occurring just before 320001.
Ans: 

The three consecutive whole numbers occurring just before 320001 are:

320001−1 = 320000−1 = 319999−1 = 319998

These are : 320000, 319999, 319998

Q.2. Find the coordinates of points A, B, C, D from the following graph.

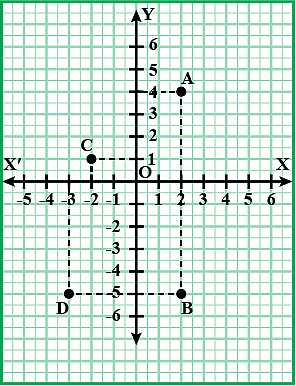
Ans: 

Q.3. Find the following products, using distributive laws: 472×1097

Ans: Using distributive law of multiplication over addition