Working with Percentages | Mathematics for GCSE/IGCSE - Class 10 PDF Download

Percentage Increases & Decreases

How do I increase or decrease by a percentage?

Identifying "before" & "after" Quantities:

• When working with percentages, consider adding to (or subtracting from) 100.
• A percentage increase of 25% means adding 25% to the original amount.
• A percentage decrease of 25% means subtracting 25% from the original amount.

Calculating New Amounts:

• To calculate a 25% increase, find 125% of the "before" price by adding 25% to the original amount.
• To calculate a 25% decrease, find 75% of the "before" price by subtracting 25% from the original amount.

Percentage Increase:

• For a 25% increase, add 25% to the original amount.
  • Example: If you have $100 and want to increase it by 25%, you would add $25 to get $125.

Percentage Decrease:

• For a 25% decrease, subtract 25% from the original amount.
  • Example: If you have $100 and want to decrease it by 25%, you would subtract $25 to get $75.

Using Multipliers:

• A multiplier, represented as 'p', is the decimal equivalent of a percentage increase or decrease.
• For a 25% increase, the multiplier is 1.25. Multiply the original amount by 1.25 to find the new amount.
• For a 25% decrease, the multiplier is 0.75. Multiply the original amount by 0.75 to find the new amount.

Application of Multipliers:

• The formula relating the amount "before" and "after" a percentage change is expressed as "before" × p = "after," where p represents the multiplier.

How do I find a percentage change?

• Method 1: Reorganizing the Formula:
  • Rearrange the formula "before" × p = "after" to make p (the multiplier) the subject.
  • 
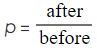
  • Calculate the value of p and interpret its significance.
    • p = 1.02 indicates a 2% increase.
    • p = 0.97 indicates a 3% decrease.
• Method 2: Understanding Percentage Change
  • Use the formula that the "percentage change" is .
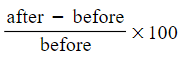  • A positive value signifies a percentage increase.
  • A negative value indicates a percentage decrease.
  • This formula is also applicable for percentage profit or loss.
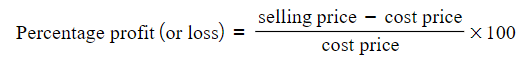
    • the "cost" price is the price a shop has to pay to buy something and the "selling" price is how much the shop sells it for
      
  • You can identify whether there is a profit or loss 
    • cost price < selling price = profit (formula gives a positive value)
    • cost price > selling price = loss (formula gives a negative value)

Reverse Percentages

What is a reverse percentage?

• A reverse percentage problem involves determining the original value before a percentage increase or decrease.

Steps to Solve Reverse Percentage Questions

• Consider the original quantity, even if it's not explicitly provided in the question.
• Determine the percentage change as a multiplier, denoted by 'p'. For instance, a 4% increase translates to p = 1 + 0.04 = 1.04, while a 5% decrease corresponds to p = 1 - 0.05 = 0.95.
• Formulate the equation 'original quantity × p = final quantity' to represent the relationship between the two.
• Ensure the order is correct: the change affects the original quantity, not the final one.
• Rearrange the equation to isolate the original quantity by dividing the final quantity by the multiplier, 'p'.