Simultaneous Equations | Mathematics for GCSE/IGCSE - Year 11 PDF Download

Linear Simultaneous Equations

What are linear simultaneous equations?

• Linear simultaneous equations involve two unknowns, typically represented as x and y.
  • To solve for both variables, you need two equations that can be solved simultaneously.
    • For instance, consider the equations 3x - 2y = 11 and 2x - y = 5.
    • By solving these equations together, you can determine that x = 3 and y = 1.
• If they just have x and y in them (no x² or y² or xy etc) then they are linear simultaneous equations

Clear all your Year 11 doubts with EduRev Join for Free

Join for Free

How do I solve linear simultaneous equations by elimination?

• "Elimination" involves eliminating one of the variables, x or y, from the equations. For instance:
• To eliminate the x's from 3x - 2y = 11 and 2x - y = 5, follow these steps:
  • Multiply every term in the first equation by 2: 6x - 4y = 22
  • Multiply every term in the second equation by 3: 6x - 3y = 15
  • Subtract the second result from the first to eliminate the 6x's, resulting in 4y - (-3y) = 22 - 15, simplifying to 7y = 7
  • Solve for y (y = 1) and substitute y = 1 back into either original equation to find x (x = 3)
• To eliminate the y's, follow a similar process:
  • Multiply every term in the second equation by 2: 4x - 2y = 10
  • Add this result to the first equation to eliminate the 2y's, as 2y - 2y = 0
  • Continue solving for x and y as described above
• Check your final solutions satisfy both equations.

How do I solve linear simultaneous equations by substitution?

• "Substitution" means substituting one equation into the other
• Solve 3x + 2y = 11 and 2x - y = 5 by substitution
  • Rearrange one of the equation into y = ... (or x = ...)
    • For example, the second equation becomes y = 2x - 5 
  • Substitute this into the first equation (replace all y's with 2x - 5 in brackets)
    • 3x + 2(2x - 5) = 11
  • Solve this equation to find x (x = 3), then substitute x = 3 into y = 2x - 5 to find y (y = 1)
• Check your final solutions satisfy both equations

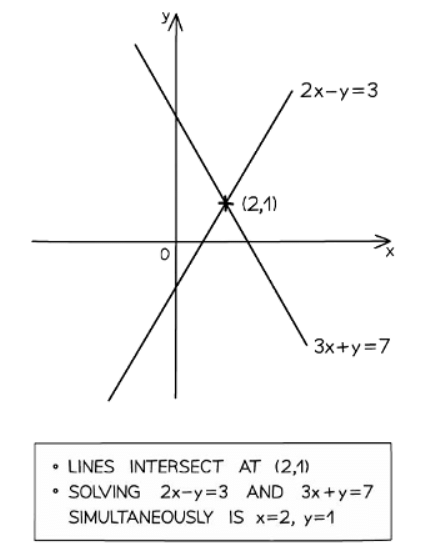
How do you use graphs to solve linear simultaneous equations?

• Plot both equations on the same set of axes. You can use a table of values or rearrange them into y = mx + c form if needed.
• Find where the lines intersect. The solutions to the simultaneous equations are the coordinates of this point of intersection.
• For example, consider solving 2x - y = 3 and 3x - y = 4 simultaneously. After plotting and finding the intersection point (2, 1), the solution is x = 2 and y = 1.

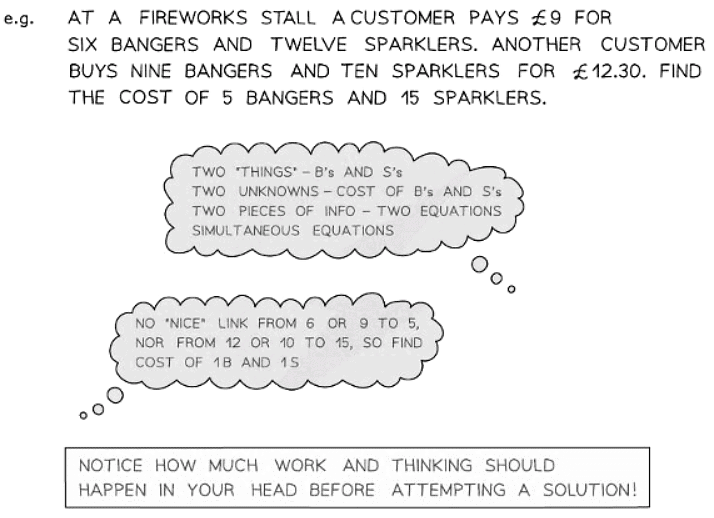
How do I solve linear simultaneous equations from worded contexts?

Download the notes Simultaneous Equations

Download as PDF

Download as PDF

Quadratic Simultaneous Equations

What are quadratic simultaneous equations?

• When there are two unknowns (say x and y) in a problem, we need two equations to be able to find them both: these are called simultaneous equations
• If there is an x² or y² or xy in one of the equations, then they are quadratic (or non-linear) simultaneous equations

Take a Practice Test Test yourself on topics from Year 11 exam

Practice Now

Practice Now

How do I solve quadratic simultaneous equations?

Steps to Solve Quadratic Simultaneous Equations:

• Using the Substitution Method:
  • Substitute the linear equation, either y = ... or x = ..., into the quadratic equation, avoiding the reverse substitution.
• Key Steps:
  • Solve x² - y² = 25 and y - 2x = 5.
  • Rearrange the linear equation to y = 2x - 5.
  • Replace all y's with (2x - 5) in brackets in the quadratic equation: x² - (2x - 5)² = 25.
  • Expand and solve the quadratic equation to find x = 0 and x = -4.
  • Substitute each x value into y = 2x - 5 to determine the corresponding y value.
  • Present solutions clearly: x = 0, y = 5 or x = -4, y = -3.
• Check your final solutions satisfy both equations.

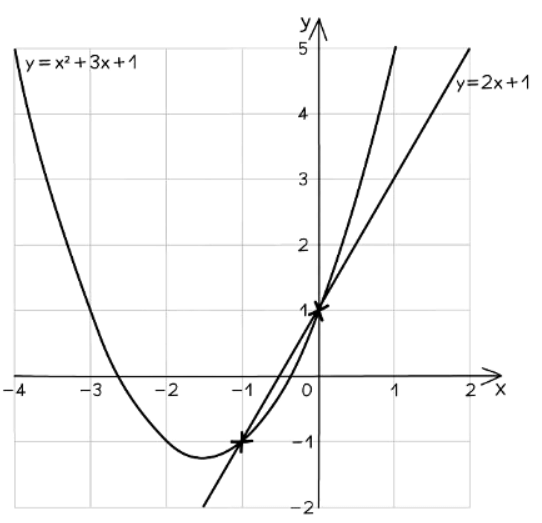
How do you use graphs to solve quadratic simultaneous equations?

• When plotting two equations on the same set of axes, a table of values can be utilized. For linear equations, it may be beneficial to rearrange them into the form y = mx + c.
• Locate the points where the lines intersect. These points represent the solutions to the simultaneous equations, providing the coordinates of the intersection.
• For instance, consider solving the equations y = x^2 - 3x - 1 and y = 2x - 1 simultaneously. By plotting both equations and finding their points of intersection at (-1, -1) and (0, 1), the solutions emerge as x = -1, y = -1 or x = 0, y = 1.