Class 10 Exam > Class 10 Notes > Mathematics for GCSE/IGCSE > Types of Sequences
Types of Sequences | Mathematics for GCSE/IGCSE - Class 10 PDF Download
Types of Sequences
What types of sequences are there?
- Linear and quadratic sequences have their own specific notes.
- Other types of sequences include geometric and Fibonacci sequences, which are examined in more detail below.
- Additional sequences include cube numbers (cubic sequences) and triangular numbers.
- A common type of sequence in exam questions involves fractions combined with the above types.
- Always look for features that make the position-to-term and term-to-term rules easy to identify.
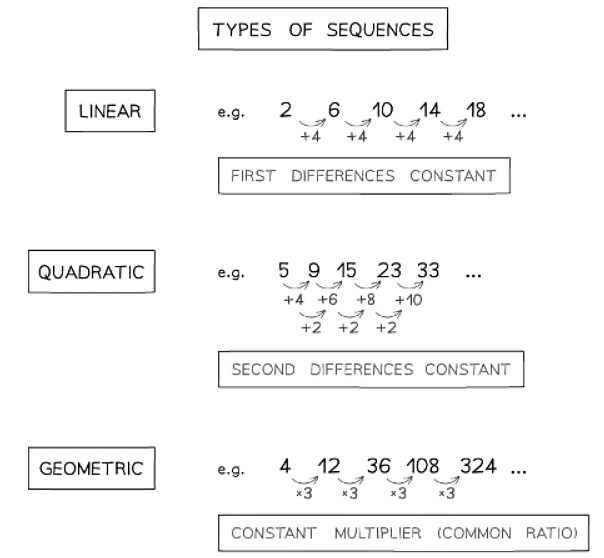

What is a geometric sequence?
- A geometric sequence can also be referred to as a geometric progression and sometimes as an exponential sequence
- In a geometric sequence, the term-to-term rule would be to multiply by a constant, r
- an+1 = r.an
- r is called the common ratio and can be found by dividing any two consecutive terms, or
- r = an+1 / an
- In the sequence 4, 8, 16, 32, 64, ... the common ratio, r, would be 2 (8 ÷ 4 or 16 ÷ 8 or 32 ÷ 16 and so on)

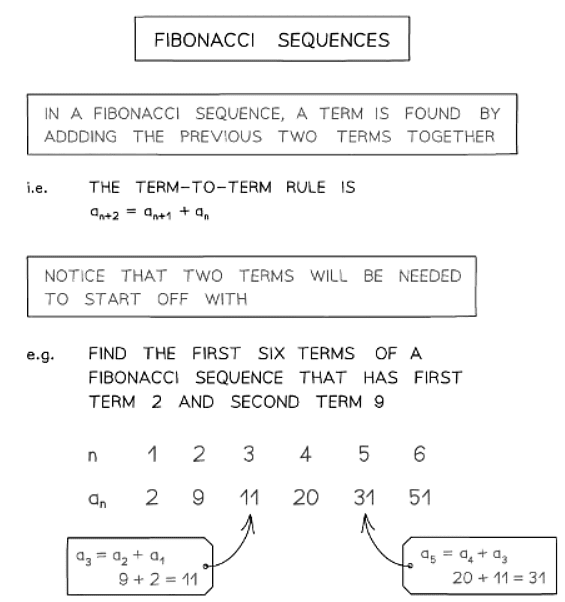
What is a Fibonacci sequence?
- The Fibonacci sequence is: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...
- The sequence begins with the first two terms as 1.
- Each subsequent term is the sum of the previous two terms.
- The term-to-term rule is an+2 = an+1 + an
- Two initial terms are needed to start a Fibonacci sequence.
- Any sequence with the term-to-term rule of adding the previous two terms is considered a Fibonacci sequence, even if the first two terms are not both 1.
- Fibonacci sequences often appear in nature, such as in the number of petals on flowers.
What is a cubic sequence?
- In a cubic sequence, the first differences between terms are not constant.
- The second differences (differences between the first differences) are also not constant.
- The third differences (differences between the second differences) are constant.
- Another way to understand this is that in a cubic sequence, the sequence of second differences forms a linear sequence.
- Example:
- Sequence: 1, 5, 21, 55, 113, …
- 1st Differences: 4, 16, 34, 58 (a Quadratic Sequence)
- 2nd Differences: 12, 18, 24 (a Linear Sequence)
- 3rd Differences: 6, 6, 6 (Constant)
- Constant third differences indicate a cubic sequence.
What should I be able to do with cubic sequence?
- You should be able to recognise and continue a cubic sequence
- You should also be able to find a formula for the nth term of a simple cubic sequence in terms of n
- This formula will most likely be in one of the forms nth term = an3 or n3 + b
- To find the values of a and b, you must remember the terms in the sequence for n3 and compare them to the given sequence
- n3 is the sequence 1, 8, 27, 64, 125, ....
- Usually, each term will be either a little bit more or less than the sequence for n3
- For example, the sequence 2, 9, 28, 65, 126, , ... has the formula n3 + 1 as each term is 1 more than the corresponding term in n3
- Sometimes, each term will be two or three times the term in the sequence for n3
- For example, the sequence 2, 16, 54, 128, 250, ... has the formula 2n3 as each term is twice the corresponding term in n3
Problem solving and sequences
- When the nature of the sequence is identified, it becomes feasible to determine unknown terms within the sequence.
- This process often involves setting up and solving equations, which might include simultaneous equations.
- Furthermore, some problems may entail sequences that correlate with well-known number sequences like square numbers, cube numbers, and triangular numbers.


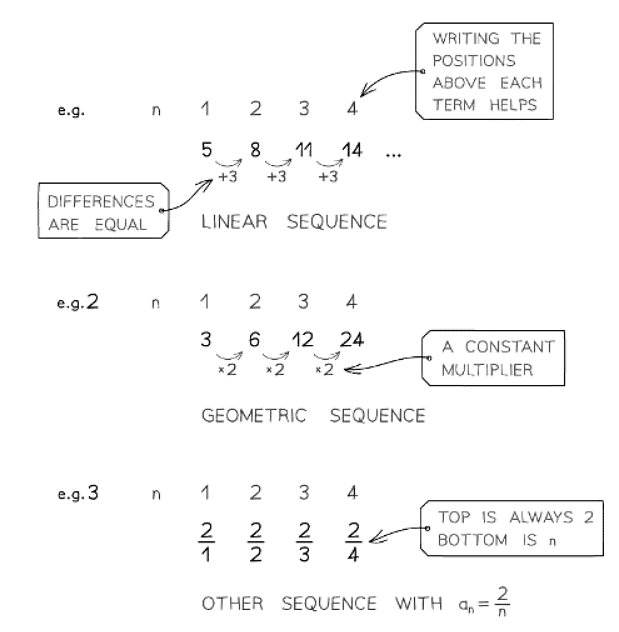
Identifying Sequences
How do I identify a sequence?
- Is it clear from the given information?
- Does the question explicitly state it?
- Do you notice a consistent number that you use to transition from one term to the next?
- If there is, then it's likely a geometric sequence.
- Then, observe the variances between the terms.
- If the first differences remain constant, it's indicative of a linear sequence.
- If the second differences remain constant, it's indicative of a quadratic sequence.
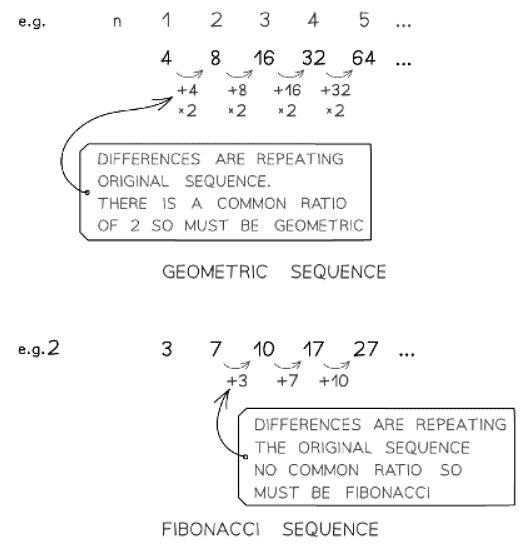
- Special cases to be aware of:
- If the differences repeat the original sequence
- It is a geometric sequence with common ratio 2
- Fibonacci sequences also have differences that repeat the original sequence
- However questions usually indicate if a Fibonacci sequence is involved
How do I continue a given sequence?
Let's break down the approach to finding the next terms or filling in gaps within a sequence.
- CASE 1: Start by checking if there's a consistent difference between terms. If there is, it's a linear sequence. Simply add or subtract this common difference to each term to find the next ones. This approach follows the term-to-term rule.
- CASE 2: If there's no consistent difference, check if there's a common second or third difference. If so, it's a quadratic or cubic sequence respectively. Determine the next term by first identifying the next difference and then adding it to the sequence.
- CASE 3: If there's neither a common second nor third difference, inspect if there's a common multiplier between terms, indicating a geometric sequence. Find the next term by multiplying the last term by this common multiplier.
- CASE 4: Some sequences may not fit into these categories. In such cases, look for patterns in the differences. For instance, the differences may form a geometric sequence, which can help determine the next difference and subsequently, the next value in the sequence.
- In scenarios where you're asked to fill in gaps within a sequence, utilize the provided information to discern the sequence type and then proceed to complete the missing terms accordingly.
The document Types of Sequences | Mathematics for GCSE/IGCSE - Class 10 is a part of the Class 10 Course Mathematics for GCSE/IGCSE.
All you need of Class 10 at this link: Class 10
|
42 videos|395 docs|19 tests
|
FAQs on Types of Sequences - Mathematics for GCSE/IGCSE - Class 10
| 1. What are the types of sequences covered in the CIE IGCSE Maths: Extended exam? |  |
Ans. The types of sequences covered in the CIE IGCSE Maths: Extended exam include cubic sequences, arithmetic sequences, and geometric sequences.
| 2. How can one recognize and extend cubic sequences in the exam? |  |
Ans. To recognize and extend cubic sequences in the exam, one should look for patterns in the sequence where the difference between consecutive terms is not constant but follows a cubic pattern. Extending the sequence involves identifying the rule governing the cubic pattern and applying it to find the next terms.
| 3. How are 2nd differences used in identifying sequences in the exam? |  |
Ans. 2nd differences are used in identifying sequences by calculating the differences between consecutive terms in a sequence and then calculating the differences between those differences. If the 2nd differences are constant, it indicates a quadratic sequence. If the 2nd differences are not constant but follow a pattern, it can help in identifying the type of sequence.
| 4. How can one differentiate between arithmetic and geometric sequences in the exam? |  |
Ans. In arithmetic sequences, there is a common difference between consecutive terms, while in geometric sequences, there is a common ratio between consecutive terms. To differentiate between the two in the exam, one should calculate the differences between terms and see if they form a constant sequence (arithmetic) or if they form a geometric progression with a common ratio.
| 5. How important is understanding sequences and patterns for the CIE IGCSE Maths: Extended exam? |  |
Ans. Understanding sequences and patterns is crucial for the CIE IGCSE Maths: Extended exam as questions related to different types of sequences often appear. Being able to recognize, extend, and identify the patterns in sequences can help in solving problems effectively and accurately.
Related Searches
















