Class 10 Exam > Class 10 Notes > Mathematics for GCSE/IGCSE > Coordinate Geometry
Coordinate Geometry | Mathematics for GCSE/IGCSE - Class 10 PDF Download
| Table of contents |

|
| Introduction |

|
| Midpoint of a Line |

|
| Gradient of a Line |

|
| Length of a Line |

|
Introduction
- Coordinate geometry involves studying geometric figures such as lines and shapes by using coordinates.
- At the GCSE level, you are required to understand how to determine various aspects when given two points:
- Midpoint of a Line: The midpoint of a line segment is the point that divides the line segment into two equal parts.
- Gradient of a Line: The gradient of a line indicates how steep the line is. It's the ratio of the vertical change (rise) to the horizontal change (run) between two points on the line.
- Length of a Line: This refers to the distance between two points on the line, typically calculated using the Pythagorean theorem.
Midpoint of a Line
How do I find the midpoint of a line in two dimensions (2D)?
- The midpoint of a line is equidistant from both endpoints.
- To visualize, consider it as the average (mean) of the two coordinates.
- The midpoint of (x1, y1) and (x2, y2) is
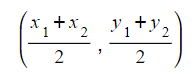
How can I extend the idea of the midpoint in two dimensions (2D)?
- The midpoint of line segment AB divides it in the ratio 1 : 1.
- When asked to find a point that divides AB in the ratio m : n, locate the point that lies
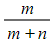 of the way from A to B.
of the way from A to B. - For example, dividing AB in the ratio 2 : 3 means finding a point that is 2/5 of the way from A to B.
- Normally an exam question will ask you to find the point that divides AB in the ratio 1 : n, so;
- find the difference between the x coordinates,
- divide this difference by [1 + n], and add the result to the x coordinate of A,
- repeat for the y coordinates.
How do I find the midpoint of a line in three dimensions (3D)?
- Finding the midpoint of a line in 3D involves a simple extension of the formula used for 2D midpoints
- Similar to before, you can think of a midpoint as being the average (mean) of three x and three y coordinates
- The midpoint of (x1, y1, z1) and (x2, y2, z2) is
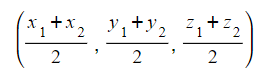
Gradient of a Line
What is the gradient of a line?
- The gradient of a line indicates how steep it is in a 2D space.
- A larger gradient value signifies a steeper line compared to a smaller gradient value.
- For example, a gradient of 3 is steeper than a gradient of 2.
- A gradient of -5 is steeper than a gradient of -4.
- A positive gradient implies the line rises from left to right.
- A negative gradient implies the line descends from left to right.
- A larger gradient value signifies a steeper line compared to a smaller gradient value.
- In the equation for a straight line, y = mx + c, the gradient is represented by m
- The gradient of y equals - 3x + 2 is −3
How do I find the gradient of a line?
- The gradient can be calculated using the formula:
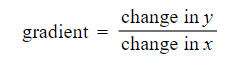
- You may see this written as
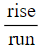 instead
instead - For two coordinates (x1, y1) and (x2, y2), the gradient of the line joining them is:
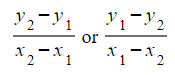
- The order of the coordinates must be consistent on the top and bottom, i.e., (Point 1 - Point 2) or (Point 2 - Point 1) for both the top and bottom.
How do I draw a line with a given gradient?
- A line with a gradient of 4 could instead be written as 4/1.
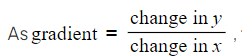 this would mean for every 1 unit to the right (x direction), the line moves upwards (y direction) by 4 units.
this would mean for every 1 unit to the right (x direction), the line moves upwards (y direction) by 4 units.- Notice that 4 also equals -4/-1, so for every 1 unit to the left, the line moves downwards by 4 units
- If the gradient was −4, then
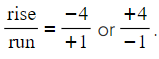 This means the line would move downwards by 4 units for every 1 unit to the right.
This means the line would move downwards by 4 units for every 1 unit to the right. - If the gradient is a fraction, for example 2/3 we can think of this as either
- For every 1 unit to the right, the line moves upwards by 2/3 , or
- For every 3 units to the right, the line moves upwards by 2.
- (Or for every 3 units to the left, the line moves downwards by 2.)
- If the gradient was
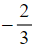 this would mean the line would move downwards by 2 units for every 3 units to the right
this would mean the line would move downwards by 2 units for every 3 units to the right - Once you know this, you can select a point (usually given, for example the y-intercept) and then count across and upwards or downwards to find another point on the line, and then join them with a straight line
Length of a Line
How do I calculate the length of a line?
- The distance between two points with coordinates (x1, y1) and (x2, y2) can be found using the formula
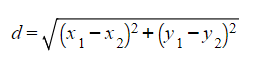
- This formula is really just Pythagoras’ Theorem a2 = b2 + c2 squared, applied to the difference in the x-coordinates and the difference in the y-coordinates;

- You may be asked to find the length of a diagonal in 3D space. This can be answered using 3D Pythagoras
The document Coordinate Geometry | Mathematics for GCSE/IGCSE - Class 10 is a part of the Class 10 Course Mathematics for GCSE/IGCSE.
All you need of Class 10 at this link: Class 10
|
38 videos|413 docs|19 tests
|
FAQs on Coordinate Geometry - Mathematics for GCSE/IGCSE - Class 10
| 1. What is the formula for finding the midpoint of a line segment in coordinate geometry? |  |
Ans. The formula for finding the midpoint of a line segment in coordinate geometry is:
Midpoint = ((x1 + x2) / 2, (y1 + y2) / 2), where (x1, y1) and (x2, y2) are the coordinates of the endpoints of the line segment.
| 2. How can a line segment be divided in a given ratio using coordinate geometry? |  |
Ans. To divide a line segment in a given ratio using coordinate geometry, you can use the section formula. The coordinates of the point dividing the line segment in the ratio m:n are:
(x, y) = ((mx2 + nx1) / (m + n), (my2 + ny1) / (m + n)), where (x1, y1) and (x2, y2) are the coordinates of the endpoints of the line segment.
| 3. What is the formula for finding the midpoint of a line in three dimensions (3D)? |  |
Ans. The formula for finding the midpoint of a line in three dimensions (3D) is:
Midpoint = ((x1 + x2) / 2, (y1 + y2) / 2, (z1 + z2) / 2), where (x1, y1, z1) and (x2, y2, z2) are the coordinates of the endpoints of the line.
| 4. How is the gradient of a line calculated in coordinate geometry? |  |
Ans. The gradient of a line in coordinate geometry is calculated using the formula:
Gradient = (change in y) / (change in x) = (y2 - y1) / (x2 - x1), where (x1, y1) and (x2, y2) are the coordinates of two points on the line.
| 5. How can the gradient of a line help in understanding the direction and steepness of the line in coordinate geometry? |  |
Ans. The gradient of a line indicates the direction and steepness of the line in coordinate geometry. A positive gradient indicates an upward slope, a negative gradient indicates a downward slope, and a gradient of zero indicates a horizontal line. The larger the absolute value of the gradient, the steeper the line.
Related Searches















