Year 11 Exam > Year 11 Notes > Mathematics for GCSE/IGCSE > Problem Solving with Differentiation
Problem Solving with Differentiation | Mathematics for GCSE/IGCSE - Year 11 PDF Download
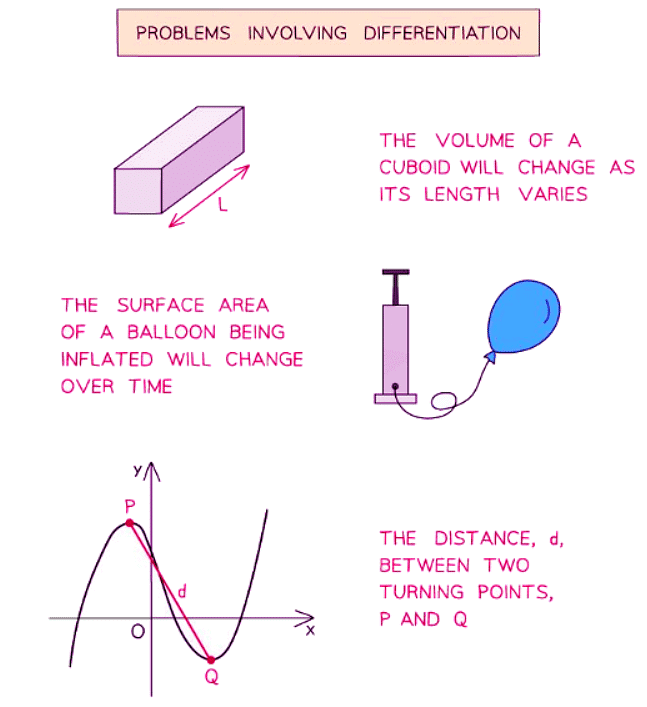
What problems could involve differentiation?
- Differentiation allows us to analyze how one quantity changes concerning another.
- The derived function, also known as the gradient function or derivative, provides a measure of the rate of change.
- Various problems involving a variable quantity can be addressed through differentiation. For instance:
- How the area of a rectangle changes as its length varies.
- How the volume of a cylinder changes as its radius varies.
- How the position of a car changes over time, indicating its speed.
- Additionally, differentiation can be applied to problems based on the graph of a curve, such as determining:
- The distance between two turning points on the curve.
- The area of a shape formed by points on the curve, like turning points and axis intercepts.
How do I solve problems involving differentiation?
Problems generally fall into two categories:
1. Graph-based problems
- These problems are based around the graph of a curve and its turning points.
 |
Download the notes
Problem Solving with Differentiation
|
Download as PDF |
Download as PDF
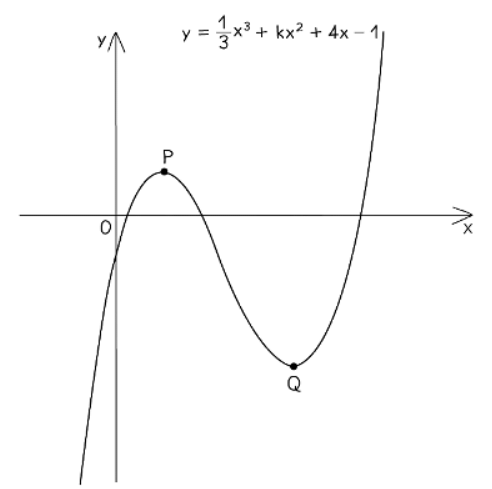
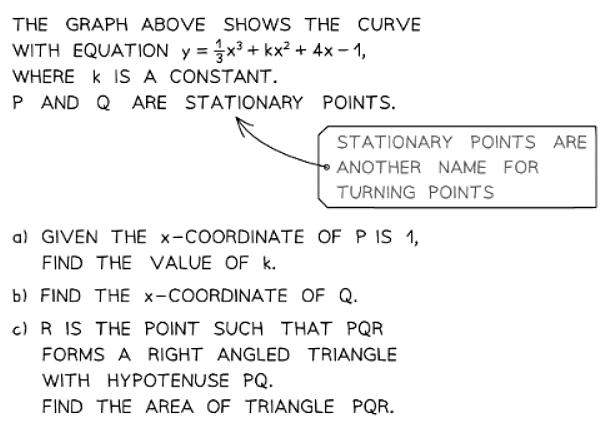
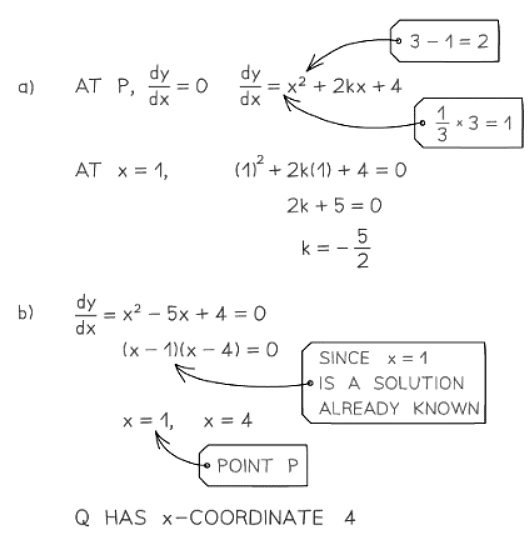
2. Maximum/Minimum problems
- The maximum or minimum values hold significance in the context of the problem:
- For instance, the maximum volume of a box formed from a flat sheet of material or the minimum height of water in a reservoir.
- These scenarios are often referred to as optimization problems.
- The maximum or minimum value represents the optimal or best solution to the problem.
Question for Problem Solving with Differentiation
Try yourself:
How can differentiation be applied to determine the maximum or minimum values in a problem?View Solution
The document Problem Solving with Differentiation | Mathematics for GCSE/IGCSE - Year 11 is a part of the Year 11 Course Mathematics for GCSE/IGCSE.
All you need of Year 11 at this link: Year 11
|
84 videos|120 docs
|
FAQs on Problem Solving with Differentiation - Mathematics for GCSE/IGCSE - Year 11
| 1. What are some common problems that could involve differentiation? |  |
| 2. How can I solve problems involving differentiation? | |
Ans. To solve problems involving differentiation, you first need to understand the basic rules of differentiation, such as the power rule, product rule, quotient rule, and chain rule. You then apply these rules to find the derivative of the given function and use it to solve the specific problem at hand.
| 3. How do I find the maximum or minimum values of a function using differentiation? | |
Ans. To find the maximum or minimum values of a function using differentiation, you first find the critical points by setting the derivative equal to zero and solving for x. You then determine whether these critical points correspond to a maximum, minimum, or neither by using the second derivative test or analyzing the behavior of the function around these points.
| 4. What is the significance of rates of change in differentiation problems? | |
Ans. Rates of change play a crucial role in differentiation problems as they help us understand how a function is changing at a particular point. By finding the derivative of a function, we can determine the rate at which the function is increasing or decreasing, which can be useful in various real-world applications such as physics, economics, and biology.
| 5. How can I calculate the slope of a curve at a specific point using differentiation? | |
Ans. To calculate the slope of a curve at a specific point using differentiation, you first find the derivative of the function. Then, you substitute the x-coordinate of the point into the derivative to find the slope of the tangent line at that point, which represents the slope of the curve at that specific point.
Related Exams
About this Document
Apr 12, 2025
Last updated
Document Description: Problem Solving with Differentiation for Year 11 2025 is part of Mathematics for GCSE/IGCSE preparation.
The notes and questions for Problem Solving with Differentiation have been prepared according to the Year 11 exam syllabus. Information about Problem Solving with Differentiation covers topics
like What problems could involve differentiation?, How do I solve problems involving differentiation? and Problem Solving with Differentiation Example, for Year 11 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Problem Solving with Differentiation.
Introduction of Problem Solving with Differentiation in English is available as part of our Mathematics for GCSE/IGCSE
for Year 11 & Problem Solving with Differentiation in Hindi for Mathematics for GCSE/IGCSE course.
Download more important topics related with notes, lectures and mock test series for Year 11
Exam by signing up for free. Year 11: Problem Solving with Differentiation | Mathematics for GCSE/IGCSE - Year 11
Description
Full syllabus notes, lecture & questions for Problem Solving with Differentiation | Mathematics for GCSE/IGCSE - Year 11 - Year 11 | Plus excerises question with solution to help you revise complete syllabus for Mathematics for GCSE/IGCSE | Best notes, free PDF download
Information about Problem Solving with Differentiation
In this doc you can find the meaning of Problem Solving with Differentiation defined & explained in the simplest way possible. Besides explaining types of
Problem Solving with Differentiation theory, EduRev gives you an ample number of questions to practice Problem Solving with Differentiation tests, examples and also practice Year 11
tests
Related Searches
Extra Questions
,Sample Paper
,Free
,MCQs
,Summary
,study material
,Problem Solving with Differentiation | Mathematics for GCSE/IGCSE - Year 11
,past year papers
,Problem Solving with Differentiation | Mathematics for GCSE/IGCSE - Year 11
,shortcuts and tricks
,practice quizzes
,Previous Year Questions with Solutions
,Objective type Questions
,Problem Solving with Differentiation | Mathematics for GCSE/IGCSE - Year 11
,mock tests for examination
,ppt
,Viva Questions
,Important questions
,Semester Notes
,Exam
,video lectures
;
Additional Information about Problem Solving with Differentiation for Year 11 Preparation
Problem Solving with Differentiation Free PDF Download
The Problem Solving with Differentiation is an invaluable resource that delves deep into the core of the Year 11 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Problem Solving with Differentiation now and kickstart your journey towards success in the Year 11 exam.
Importance of Problem Solving with Differentiation
The importance of Problem Solving with Differentiation cannot be overstated, especially for Year 11 aspirants.
This document holds the key to success in the Year 11 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Problem Solving with Differentiation Notes
Problem Solving with Differentiation Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Problem Solving with Differentiation.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Problem Solving with Differentiation Notes on EduRev are your ultimate resource for success.
Problem Solving with Differentiation Year 11 Questions
The "Problem Solving with Differentiation Year 11 Questions" guide is a valuable resource for all aspiring students preparing for the
Year 11 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Problem Solving with Differentiation on the App
Students of Year 11 can study Problem Solving with Differentiation alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Problem Solving with Differentiation,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Problem Solving with Differentiation is prepared as per the latest Year 11 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup