Class 10 Exam > Class 10 Notes > Mathematics for GCSE/IGCSE > Symmetry
Symmetry | Mathematics for GCSE/IGCSE - Class 10 PDF Download
| Table of contents |

|
| Introduction |

|
| Rotational Symmetry |

|
| Lines of Symmetry |

|
| Planes of Symmetry |

|
Introduction
Symmetry in mathematics can be of two types:
- Line (or Plane) symmetry deals with reflections and mirror images of shapes in both 2D and 3D.
- Rotational symmetry deals with how often a shape looks identical (congruent) when it has been rotated.
Rotational Symmetry
What is (the order of) rotational symmetry?
- Rotational symmetry pertains to how many times a shape appears identical as it's rotated 360° around its center.
- This quantity is termed the order of rotational symmetry.
- Utilizing tracing paper can facilitate determining the order of rotational symmetry.
- Create an arrow on the tracing paper to aid in recognizing when the rotation completes a full 360° turn.
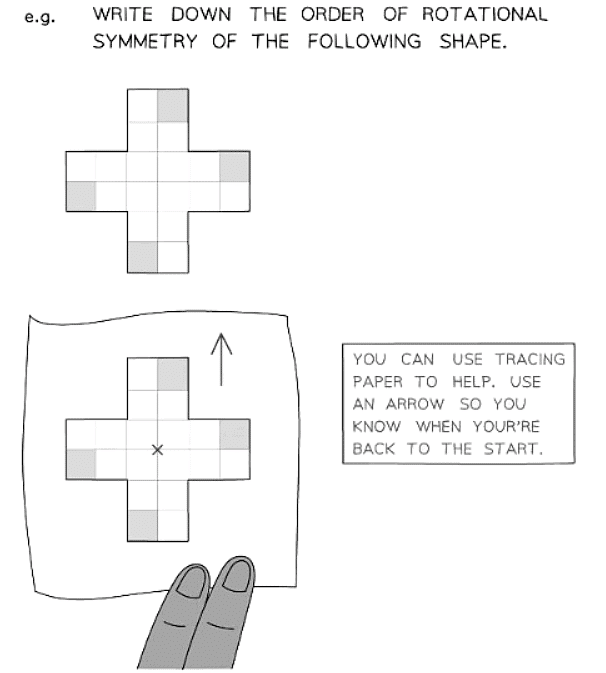
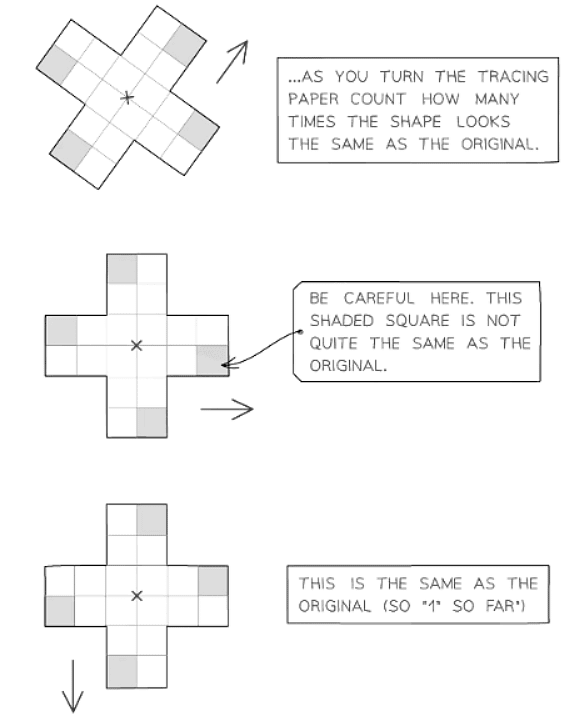
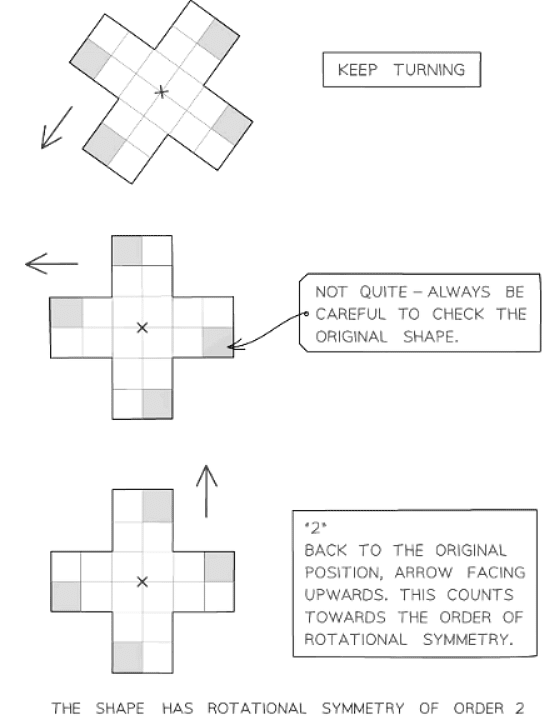
- When a shape returns to its original form after a rotation, it adds 1 to the order of rotational symmetry.
- Consequently, a shape cannot have an order of 0, as it always retains its original form after a full rotation.
- A shape characterized by rotational symmetry order 1 can be described as lacking any rotational symmetry.
- In essence, the shape only appears identical to its original form once the rotation completes a full circle back to the starting point.
Question for SymmetryTry yourself: What is the order of rotational symmetry?View Solution
Lines of Symmetry
- Line Symmetry: Line symmetry involves shapes that can incorporate mirror lines.
- Each side of the line of symmetry mirrors the other side.
- Reflection: Lines of symmetry can be likened to folding lines.
- Folding a shape along a line of symmetry results in both parts aligning perfectly.
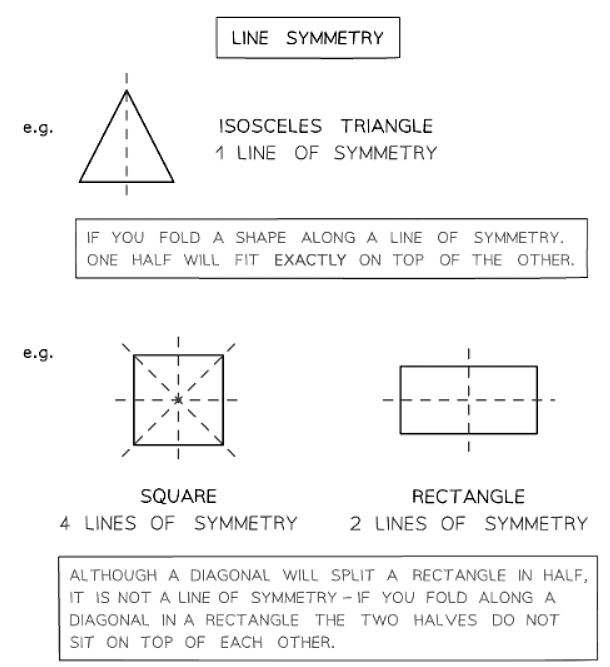
- Examining shapes from various angles can aid in understanding. Try turning the page for a different perspective.
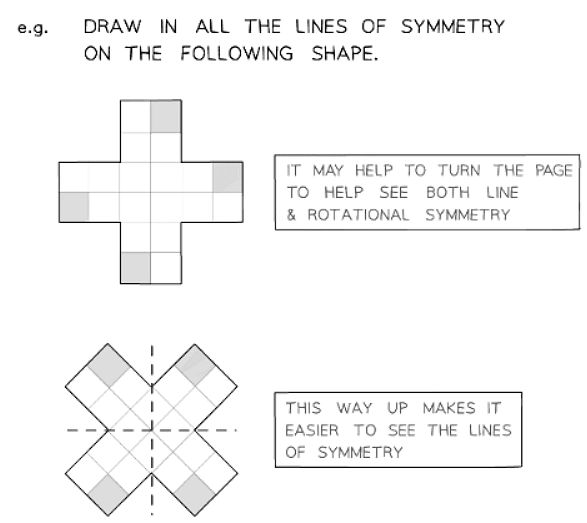
- Symmetry in Shapes
- Some questions provide a shape and a line of symmetry.
- Complete the shape by being cautious with diagonal lines of symmetry. Use tracing paper to trace the shape and reflection line, then flip to observe the reflection.
- Be mindful of diagonal lines of symmetry. Use tracing paper to trace the shape and reflection line, then flip to see the reflection.
- Two-Way Reflections
- "Two-way" reflections occur when the line of symmetry passes through the shape.



How do I solve problems involving symmetry?
- Symmetry aids in solving missing length and angle problems.
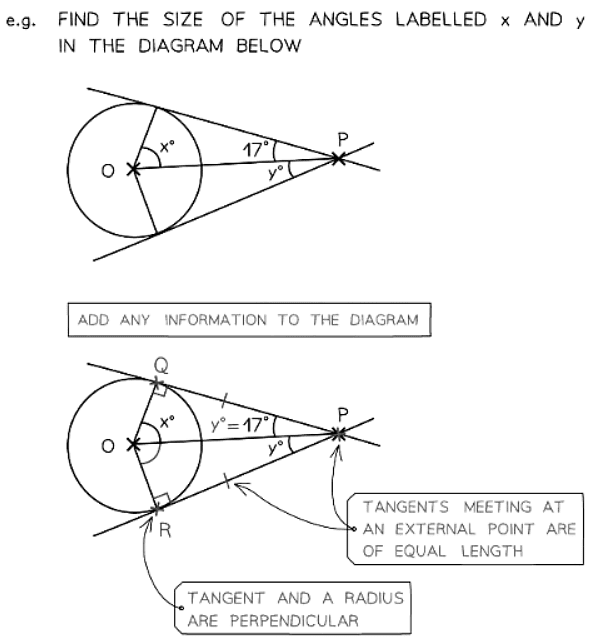
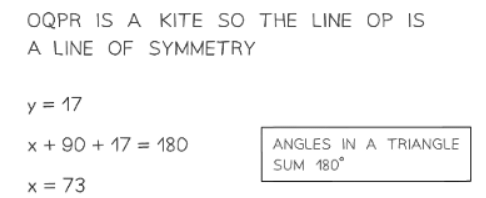
- It's helpful to draw a diagram and add lines of symmetry or supplement a given diagram with lines of symmetry. Utilize tracing paper provided during exams for assistance.
- Tracing paper can be used to enhance problem-solving by aiding in understanding symmetry.
Planes of Symmetry
What is a plane of symmetry?
- A plane represents a flat surface that can take on any 2D shape.
- A plane of symmetry is a flat plane that divides a 3D shape into two identical halves.
- If a 3D shape possesses a plane of symmetry, it also exhibits reflection symmetry, where the two halves are mirror images of each other.
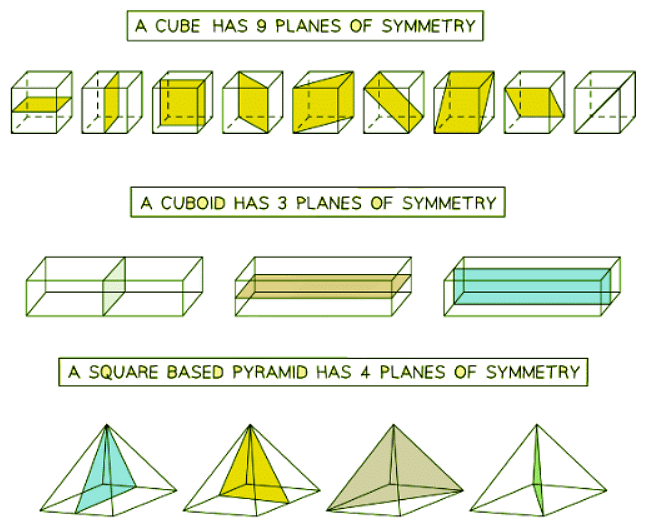
- All prisms possess at least one plane of symmetry.
- Cubes boast 9 planes of symmetry.
- Cuboids feature 3 planes of symmetry.
- Cylinders possess an infinite number of planes of symmetry.
- The quantity of planes of symmetry in other prisms corresponds to the number of lines of symmetry in their cross-section plus 1.
- Pyramids can also have planes of symmetry.
- The number of planes of symmetry in other pyramids aligns with the number of lines of symmetry in their 2D base.
- If the base of the pyramid is a regular polygon with n sides, it will have n planes of symmetry.
The document Symmetry | Mathematics for GCSE/IGCSE - Class 10 is a part of the Class 10 Course Mathematics for GCSE/IGCSE.
All you need of Class 10 at this link: Class 10
|
66 videos|674 docs|19 tests
|
FAQs on Symmetry - Mathematics for GCSE/IGCSE - Class 10
| 1. What is rotational symmetry? |  |
Ans. Rotational symmetry is a type of symmetry where an object can be rotated by a certain angle (usually less than 360 degrees) and still look the same as its original position.
| 2. How can we determine the number of lines of symmetry in a shape? |  |
Ans. The number of lines of symmetry in a shape can be determined by identifying the lines that divide the shape into two identical halves. Each line of symmetry represents a reflectional symmetry in the shape.
| 3. What are planes of symmetry in 3D shapes? |  |
Ans. Planes of symmetry in 3D shapes are imaginary planes that can be used to divide the shape into two identical halves. These planes are often used to determine the symmetry of complex geometric figures.
| 4. How can we identify the order of rotational symmetry in a shape? |  |
Ans. The order of rotational symmetry in a shape is determined by finding the number of times the shape can be rotated and still look the same as its original position. The order is usually denoted by an integer (e.g., 2-fold symmetry, 3-fold symmetry, etc.).
| 5. Can a shape have both rotational and reflectional symmetry? |  |
Ans. Yes, a shape can have both rotational and reflectional symmetry. This means that the shape can be rotated by a certain angle and still look the same, as well as have lines of symmetry that divide the shape into identical halves.
Related Searches















