Year 11 Exam > Year 11 Notes > Mathematics for GCSE/IGCSE > Surface Area
Surface Area | Mathematics for GCSE/IGCSE - Year 11 PDF Download
What is surface area?
- A face is a flat or curved surface that forms part of a three-dimensional shape.
- The surface area of a three-dimensional shape is the total of the areas of all its faces.
- Observe how we extend a two-dimensional concept (area) into three dimensions in this context.
How do I find the surface area of cuboids, pyramids, and prisms?
- In cuboids, polygonal-based pyramids, and polygonal-based prisms (i.e., pyramids and prisms with straight-sided bases), all faces are flat.
- To find the surface area, simply sum the areas of these flat faces.
- Drawing a 2D net of the 3D shape can be very useful when calculating surface area.
- Example:
- The base of a square-based pyramid has sides measuring 15 cm.
- The triangular faces are identical isosceles triangles, each with a height of 23 cm from the base to the top of the pyramid.
- Calculate the total surface area of the pyramid.
- Draw a net for the shape.
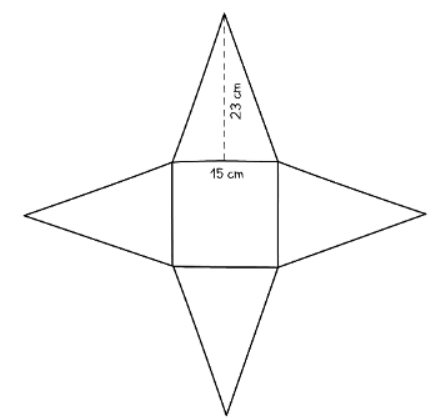
- Area of square base =152 = 225 cm2
- Area of one triangular face = ½ base × height = ½ × 15 × 23 =172.5 cm2
- Total surface area =225 + 4 × 172.5 = 915 cm2
How to find the surface area of cylinders, cones, and spheres?
- All three shapes - cylinders, cones, and spheres - have curved faces, requiring careful consideration when calculating their surface areas.
1. The net of a cylinder consists of two circles and a rectangle
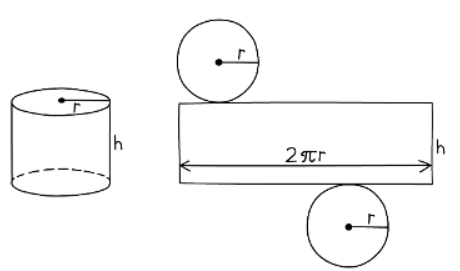
- The curved surface area of a cylinder is bold 2 πrh
- The total surface area of a cylinder with base radius r and height h is therefore given by: Total surface area of a cylinder = 2 πr2 + 2 πrh
2. The net of a cone consists of the circular base along with the curved surface area
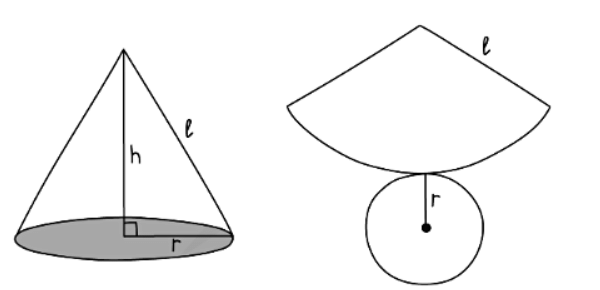
- The slant height in a cone diagram is the oblique height, whereas h represents the vertical height of the cone.
- To calculate the surface area of a cone with base radius r and slant height l, utilize the following formulas:
- Curved surface area of a cone = πrl
- Total surface area of a cone = πr2 + πrl
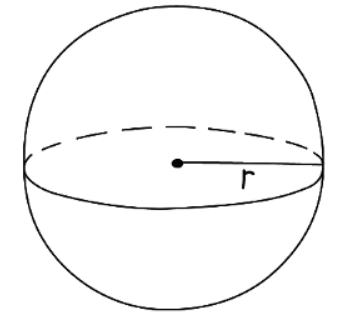
3. To find the surface area of a sphere with radius r, use the formula
- Surface area of a sphere = 4πr2
- Be careful when calculating the surface area of a hemisphere:
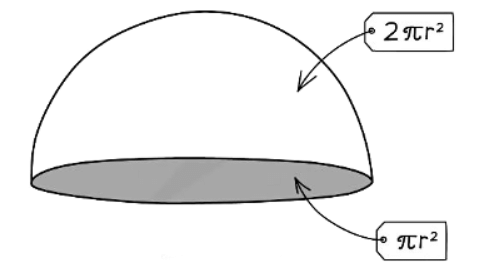
- When computing the surface area of a hemisphere, account for the curved part (half of a sphere) and the flat circular face. The total surface area is 3πr2.
The document Surface Area | Mathematics for GCSE/IGCSE - Year 11 is a part of the Year 11 Course Mathematics for GCSE/IGCSE.
All you need of Year 11 at this link: Year 11
|
84 videos|120 docs
|
FAQs on Surface Area - Mathematics for GCSE/IGCSE - Year 11
| 1. What is the formula for calculating the surface area of a cuboid? |  |
Ans. The formula for the surface area of a cuboid is 2lw + 2lh + 2wh, where l, w, and h are the length, width, and height of the cuboid, respectively.
| 2. How do you find the surface area of a pyramid? | |
Ans. To find the surface area of a pyramid, you can use the formula A = 0.5 × perimeter of base × slant height + base area, where the base area can be calculated separately depending on the shape of the base.
| 3. What is the surface area of a prism and how is it calculated? | |
Ans. The surface area of a prism is the sum of the areas of all its faces. It can be calculated by finding the area of each face and then adding them together.
| 4. Are there any shortcuts or tricks to calculating surface area quickly? | |
Ans. One shortcut for calculating the surface area of a cuboid is to add the areas of the faces in pairs (l x w, l x h, w x h) and then double the result. This can help simplify the calculation process.
| 5. How can I use the surface area formulas in real-life scenarios? | |
Ans. Understanding surface area formulas can be useful in various real-life situations, such as calculating the amount of paint needed to cover a surface, determining the material needed to construct a packaging box, or estimating the cost of materials for a construction project.
Related Exams
About this Document
|
Dec 22, 2024 Last updated |
Document Description: Surface Area for Year 11 2024 is part of Mathematics for GCSE/IGCSE preparation.
The notes and questions for Surface Area have been prepared according to the Year 11 exam syllabus. Information about Surface Area covers topics
like What is surface area?, How do I find the surface area of cuboids, pyramids, and prisms?, How to find the surface area of cylinders, cones, and spheres? and Surface Area Example, for Year 11 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Surface Area.
Introduction of Surface Area in English is available as part of our Mathematics for GCSE/IGCSE
for Year 11 & Surface Area in Hindi for Mathematics for GCSE/IGCSE course.
Download more important topics related with notes, lectures and mock test series for Year 11
Exam by signing up for free. Year 11: Surface Area | Mathematics for GCSE/IGCSE - Year 11
Description
Full syllabus notes, lecture & questions for Surface Area | Mathematics for GCSE/IGCSE - Year 11 - Year 11 | Plus excerises question with solution to help you revise complete syllabus for Mathematics for GCSE/IGCSE | Best notes, free PDF download
Information about Surface Area
In this doc you can find the meaning of Surface Area defined & explained in the simplest way possible. Besides explaining types of
Surface Area theory, EduRev gives you an ample number of questions to practice Surface Area tests, examples and also practice Year 11
tests
|
Explore Courses for Year 11 exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
study material
,shortcuts and tricks
,mock tests for examination
,Important questions
,Viva Questions
,MCQs
,past year papers
,Surface Area | Mathematics for GCSE/IGCSE - Year 11
,Exam
,Objective type Questions
,practice quizzes
,video lectures
,ppt
,Sample Paper
,Semester Notes
,Surface Area | Mathematics for GCSE/IGCSE - Year 11
,Free
,Previous Year Questions with Solutions
,Summary
,Extra Questions
,Surface Area | Mathematics for GCSE/IGCSE - Year 11
;
Additional Information about Surface Area for Year 11 Preparation
Surface Area Free PDF Download
The Surface Area is an invaluable resource that delves deep into the core of the Year 11 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Surface Area now and kickstart your journey towards success in the Year 11 exam.
Importance of Surface Area
The importance of Surface Area cannot be overstated, especially for Year 11 aspirants.
This document holds the key to success in the Year 11 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Surface Area Notes
Surface Area Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Surface Area.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Surface Area Notes on EduRev are your ultimate resource for success.
Surface Area Year 11 Questions
The "Surface Area Year 11 Questions" guide is a valuable resource for all aspiring students preparing for the
Year 11 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Surface Area on the App
Students of Year 11 can study Surface Area alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Surface Area,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Surface Area is prepared as per the latest Year 11 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup