Class 10 Exam > Class 10 Notes > Mathematics for GCSE/IGCSE > SOHCAHTOA
SOHCAHTOA | Mathematics for GCSE/IGCSE - Class 10 PDF Download
What is Trigonometry?
- Trigonometry is the branch of mathematics that deals with angles in triangles.
- It explores the relationships between the side lengths and angles of triangles.
- The term originates from the Greek words "trigonon," meaning 'triangle,' and "metron," meaning 'measure.'
What are Sin, Cos and Tan?
- The fundamental trigonometric functions - Sine, Cosine, and Tangent - originate from the ratios of side lengths within right-angled triangles.
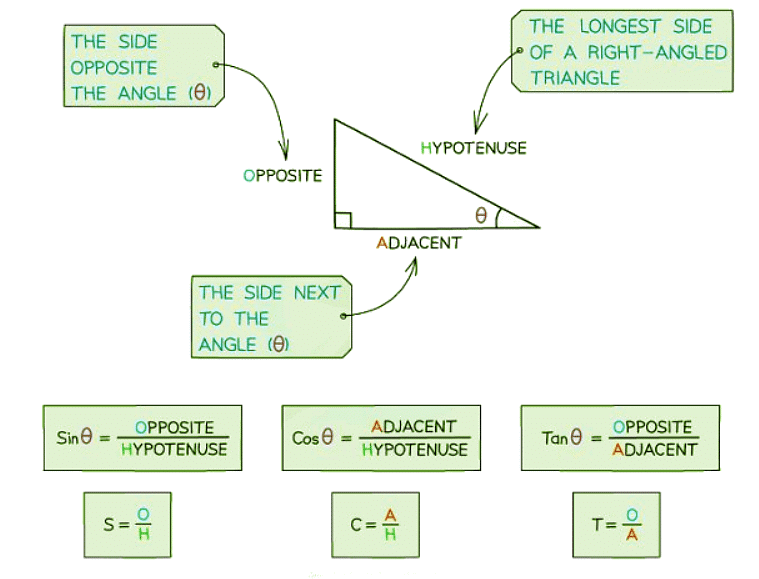
- To comprehend these ratios, it is essential to assign labels to the sides of a right-angled triangle concerning a specified angle:
- The longest side in a right-angled triangle is termed the hypotenuse (H) and always lies opposite the right angle.
- If we designate one of the other angles as θ, the side opposite θ is referred to as the opposite side (O), while the side adjacent to θ is known as the adjacent side (A).
- The functions Sine, Cosine, and Tangent represent the ratios of the lengths of these sides in the following manner.
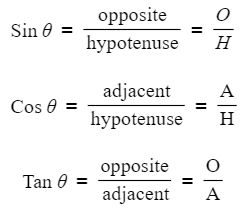
What is SOHCAHTOA?
- SOHCAHTOA is a helpful mnemonic used in trigonometry to remember trigonometric ratios.
- It stands for:
- Sine is Opposite over Hypotenuse
- Cosine is Adjacent over Hypotenuse
- Tangent is Opposite over Adjacent
- In a right-angled triangle, label one angle other than the right angle and label the sides of the triangles as follows:
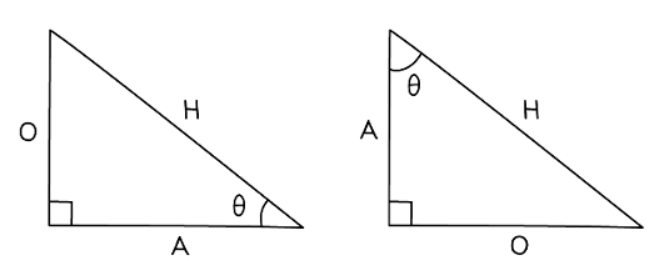
- Note that θ is the Greek letter theta. In a right-angled triangle, consider:
- O = opposite side to angle θ
- A = adjacent side next to angle θ
- H = hypotenuse - 'H' remains constant, while 'O' and 'A' vary based on the angle being referred to.
- Using those labels, the three SOHCAHTOA equations are:
How can we use SOHCAHTOA to find missing lengths?
- If you know the length of one side of a right-angled triangle and one of the angles, you can use SOHCAHTOA to find the lengths of the other sides.
- Start by labeling the sides of the triangle with H (hypotenuse), O (opposite), and A (adjacent).
- Choose the appropriate ratio based on the known values and the value you need to find.
- For example, if you know the angle and the side opposite it (O), and you need to find the hypotenuse (H), use the sine ratio.
- Substitute the known values into the chosen ratio.
- Use your calculator or knowledge of trigonometric exact values to solve for the unknown side.
How can we use SOHCAHTOA to find missing angles?
- If you know two sides of a right-angled triangle, you can utilize SOHCAHTOA to determine the size of one of the angles.
- The missing angles can be found using inverse trigonometric functions:
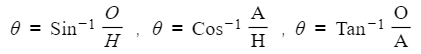
- After selecting the appropriate ratio and substituting the values, apply inverse trigonometric functions either using a calculator or trigonometric exact values to obtain the correct angle measurement.
Do sin, cos and tan work with obtuse angles?
- Your calculator or knowledge of trigonometric exact values can assist in finding sine, cosine, and tangent of any angle.
- Certain patterns can be helpful, particularly when determining obtuse angles:
- sin(x) = sin(180° - x)
- For example, sin(150°) = sin(180° - 150°) = sin(30°)
- cos(x) = -cos(180 - x)
- For example, cos(150°) = -cos(180° - 150°) = -cos(30°)
- tan(x) = -tan(180 - x)
- For example, tan(150°) = -tan(180° - 150°) = -tan(30°)
- Exercise caution when dealing with obtuse angles; calculators typically provide the acute angle, so apply the rules above to obtain the correct obtuse angle.
How do I find the shortest distance from a point to a line?
- The most direct route from any point to a line is always the perpendicular distance.
- Construct a right-angled triangle with the point, the perpendicular distance, and a point on the line, then utilize SOHCAHTOA to calculate the distance effectively.
Question for SOHCAHTOATry yourself: What does the acronym SOHCAHTOA stand for in trigonometry?View Solution
The document SOHCAHTOA | Mathematics for GCSE/IGCSE - Class 10 is a part of the Class 10 Course Mathematics for GCSE/IGCSE.
All you need of Class 10 at this link: Class 10
|
42 videos|395 docs|19 tests
|
Related Searches





















