Notes: Geometry | Mathematics & Pedagogy Paper 1 for CTET & TET Exams - CTET & State TET PDF Download
| Table of contents |

|
| Basic Geometrical Terms |

|
| Angle |

|
| Tangrams |

|
| Triangles |

|
| Circle |

|
 Geometry is a branch of mathematics concerned with the properties and relations of points, lines, surfaces, and solids. It is fundamental to many fields including art, architecture, engineering, and various branches of science. For the Central Teacher Eligibility Test (CTET), a strong understanding of geometry is essential, especially for teaching mathematics at the primary and upper primary levels.
Geometry is a branch of mathematics concerned with the properties and relations of points, lines, surfaces, and solids. It is fundamental to many fields including art, architecture, engineering, and various branches of science. For the Central Teacher Eligibility Test (CTET), a strong understanding of geometry is essential, especially for teaching mathematics at the primary and upper primary levels.
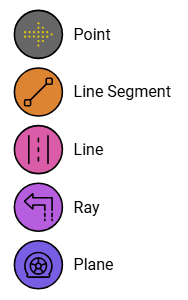
Basic Geometrical Terms
1. Point
A dot (.) represents a point.
It represents an exact location in a plane or space.
It has no length and breadth. We represent a point with a capital letter, as shown below. 2. Line Segment
2. Line Segment
Mark two points on a sheet of paper and name them as A and B. Join these points using a ruler. The figure so obtained is called a line segment. A line segment has two endpoints. It is named by the endpoints, as line segment AB or
Join these points using a ruler. The figure so obtained is called a line segment. A line segment has two endpoints. It is named by the endpoints, as line segment AB or 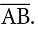
 3. Line
3. Line
A line segment extended on both the sides without an end is called a line.
A line has no endpoints. A line is denoted by taking any two points on it. For example, consider the line  To name this line, we mark any two points on it, say, A and B. Then, it is named as
To name this line, we mark any two points on it, say, A and B. Then, it is named as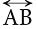 (line AB) and represented, as shown alongside.
(line AB) and represented, as shown alongside. Generally, we use the word line for a straight line.Straight line can be vertical, horizontal or slanting.
Generally, we use the word line for a straight line.Straight line can be vertical, horizontal or slanting.
4. Ray
A ray is a straight path that has one endpoint and goes on and on in one direction.
This ray begins at point A and goes through point B.
It does not stop at point B. We name the given ray as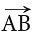 (ray AB), where the first letter is always the endpoint.
(ray AB), where the first letter is always the endpoint. The symbol → shows that a ray has a fixed endpoint and extends forever in the other direction.The rays of light from a torch and the rays of sun are the most common examples of a ray.
The symbol → shows that a ray has a fixed endpoint and extends forever in the other direction.The rays of light from a torch and the rays of sun are the most common examples of a ray. 5. Plane
5. Plane
A plane is a flat surface.
In mathematics, a plane means one that goes on and on, in all directions without an end. We usually work with just a part of a plane. Points and lines lie on a plane. A plane can be named by using any three points on it. The given figure shows plane PQR. The order of the points does not matter.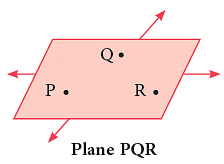 Some representations of a plane surface from your everyday life are:
Some representations of a plane surface from your everyday life are:
Types of Lines
1. Parallel lines
The lines on the same plane that never meet, no matter how far they are extended, are called parallel lines.
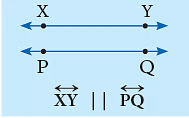 They are always the same distance apart. The symbol ‘||’ is used to show ‘‘is parallel to’’.
They are always the same distance apart. The symbol ‘||’ is used to show ‘‘is parallel to’’.
Here, line XY is parallel to line PQ and line LM || line AB.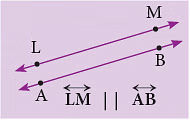 The following are some of the representations of parallel lines in everyday life:
The following are some of the representations of parallel lines in everyday life: 2. Intersecting lines
2. Intersecting lines
The lines that cross each other at a point are called intersecting lines.
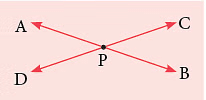 In the figure given alongside,
In the figure given alongside,  intersect at point P. The following are some examples of the intersecting lines or line segments:
intersect at point P. The following are some examples of the intersecting lines or line segments: 3. Perpendicular lines
3. Perpendicular lines
When two intersecting lines meet to form right angles, they are called perpendicular lines.
They are indicated by the symbol 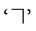 (a square corner) in the diagrams.Line AB is perpendicular to line CD and is written in short as
(a square corner) in the diagrams.Line AB is perpendicular to line CD and is written in short as 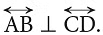
 The letter ‘L’ is an example of perpendicular line segments. ‘ ⊥ ’ is the symbol for ‘‘is perpendicular to’’.
The letter ‘L’ is an example of perpendicular line segments. ‘ ⊥ ’ is the symbol for ‘‘is perpendicular to’’.
Measuring a Line Segment
To Measure the Length of a Line Segment using a Ruler
Let us measure the line segment AB shown below. We follow the steps given below.
Step 1: Place the ruler along the line segment AB.
The zero (0) mark of the ruler should coincide with one end, point A of the line segment. Step 2: Read the mark on the ruler at the other end of the line segment, i.e., point B.
Step 2: Read the mark on the ruler at the other end of the line segment, i.e., point B.
Here, point B is at 5.5 cm mark of the ruler. So, the length of the line segment AB is 5.5 cm.
Drawing a Line Segment
To draw a line segment of a given length, say 6.8 cm, we take the following steps.
Step 1: Take a sheet of paper and mark a point, say A, on it with a sharpened pencil. Step 2: Place the ruler with its zero (0) mark at point A, as shown.
Step 2: Place the ruler with its zero (0) mark at point A, as shown.
Step 3: Put your pencil at point A and move the pencil 8 small divisions after 6. This gives a line segment AB of length 6.8 cm.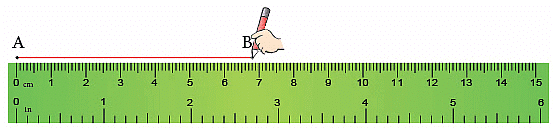
Angle
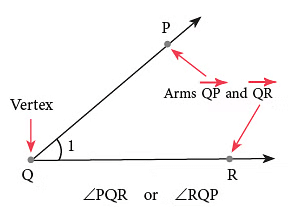
An angle is a figure formed by two rays meeting at a common endpoint.
The common endpoint is called the vertex of the angle and the two rays are called the arms of the angle.
Looking at these pictures, you can form some idea of an angle:
The symbol for angle is ∠.
1. Naming an Angle
You can name an angle in three ways:
- Using a three-letter name in the order: a point on oneray, vertex and a point on the other ray. ∠PQR or ∠RQP
- Using only one-letter name, i.e., the vertex ∠Q. (This can be used when there is only one angle with this vertex.)
- Using a number to name the angle, i.e., ∠1.
2. Interior and Exterior of an Angle
The region between the rays, that is, the inside of an angle, is called the interior of the angle and the region outside the arms of angle is called the exterior of the angle.
The point P is in the interior of the angle, whereas points S and U are in the exterior of the angle. Points Q and R lie on the arms of the angle.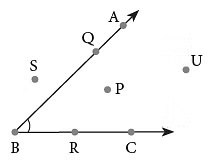
Measure the Angles
By measure of the angle, we mean the amount of rotation or turning.
 Just as there are standard units of length, area, weight, etc., there are also standard units for the measurement of angles. The standard unit of measure for angles is the degree. The symbol for degree is °.The angle formed by one complete rotation measures 360 degrees or 360°.Look at the following example. The drawings below show angles of 40°, 150° and 270°.
Just as there are standard units of length, area, weight, etc., there are also standard units for the measurement of angles. The standard unit of measure for angles is the degree. The symbol for degree is °.The angle formed by one complete rotation measures 360 degrees or 360°.Look at the following example. The drawings below show angles of 40°, 150° and 270°.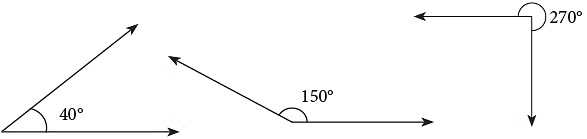
Edurev Tips: One complete rotation is divided into 360 equal parts.
The measure of one part is called one degree or 1°.
Look at the following clocks: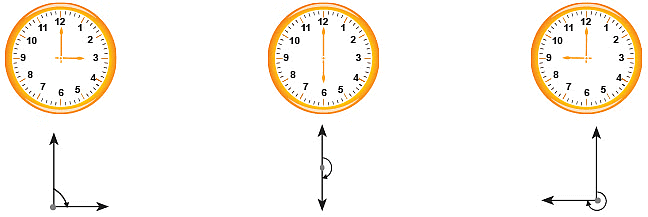 A hand of a clock turns from one position to another as it changes its direction. This change of direction or turning can be represented by drawing two arrows from one point.
A hand of a clock turns from one position to another as it changes its direction. This change of direction or turning can be represented by drawing two arrows from one point. The picture alongside shows one complete rotation.
The picture alongside shows one complete rotation.
The least amount of turning that brings the hand back to its starting position is called one complete rotation.
Example 1: If a circle is divided into 20 equal parts, what will be the measure of an angle of each part?
Angle formed by one complete rotation = 360°.
∴ Measure of angle of each of the 20 equal parts = 360° / 20 = 18°.
Example 2: Calculate the angle between neighbouring spokes on each wheel.
(a)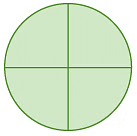 (b)
(b)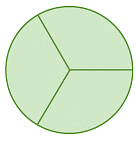 (c)
(c)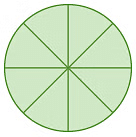
(a) As the wheel (circle) is divided into 4 equal parts, the angle between the neighbouring spokes = 360° / 4 = 90°.
(b) The wheel is divided into 3 equal parts, so the angle between the neighbouring spokes = 360° / 3 = 120°.
(c) The wheel is divided into 8 equal parts, so the angle between the neighbouring spokes = 360° / 8 = 45°.
Measuring an Angle
The instrument used for measuring angles is called a protractor.
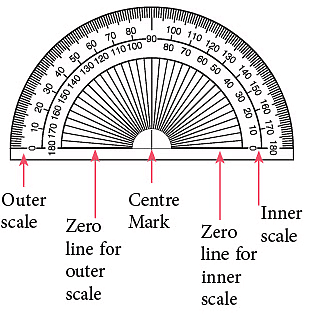 The diagram on the right shows a protractor. It has the shape of a semi-circle and the angle at the centre is divided into 180°.
The diagram on the right shows a protractor. It has the shape of a semi-circle and the angle at the centre is divided into 180°.
Edurev Tips: The inner scale of the protractor is marked from 0° to 180° anticlockwise. The outer scale of the protractor is marked from 0° to 180° clockwise. Each small division is 1°.
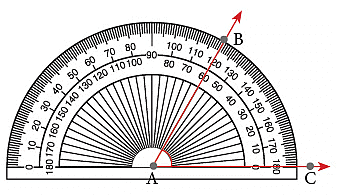
1. To Measure an Angle less than 180°
Step 1: Place the centre of the protractor at the vertex of the angle.
Step 2: Make sure that 0° line of the protractor is placed along one arm (AC) of the angle.
Step 3: Read the value on the protractor as indicated by the other arm (AB) of the angle. Thus, ∠ BAC = 60°.
2. To Measure an Angle greater than 180°
Suppose, you are required to measure ∠x.
Step 1: Measure ∠a.
Step 2: Then, reflex ∠BOC = 360° – a°.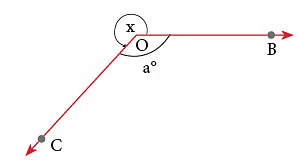
Drawing Angles using Protractor
To draw an angle that measures 80°.
Step 1: Draw any ray OA.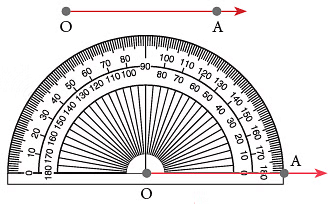 Step 2: Place the protractor such that its centre mark may fall on O, the endpoint of the ray. Align the ray with the 0° mark of one of the protractor scales. The endpoint O of the ray will be the vertex of the angle.
Step 2: Place the protractor such that its centre mark may fall on O, the endpoint of the ray. Align the ray with the 0° mark of one of the protractor scales. The endpoint O of the ray will be the vertex of the angle.
Step 3: Using the scale on which the ray OA aligns with 0°, mark the point at 80°. Label the point as B. Step 4: Remove the protractor and join B to O.
Step 4: Remove the protractor and join B to O.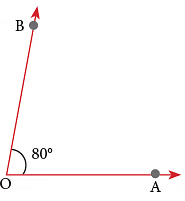 Thus, ∠AOB is the required angle.
Thus, ∠AOB is the required angle.
As you can see, we have drawn this angle using the inner scale on the protractor. What will be the angle like, if we use the outer scale on the protractor?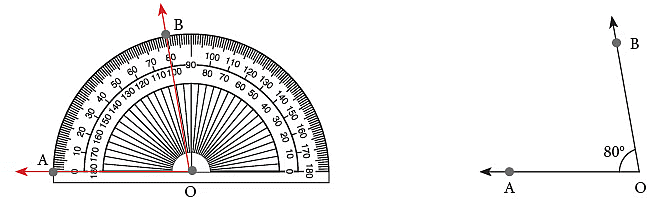 Observe the following angles.
Observe the following angles.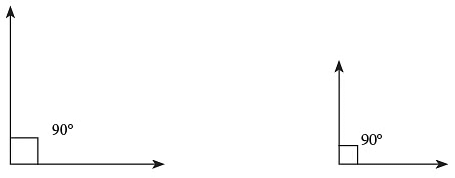 Irrespective of the length of the arms, each angle = 90°.
Irrespective of the length of the arms, each angle = 90°.
Types of Angles
Angles are named according to their measure between 90° and 180° and 180° and 360°. Look at the following illustrations. Sita sat on a roller coaster. Let her position be A. The roller coaster starts moving in an anticlockwise direction and this movement brings a change in Sita’s position.
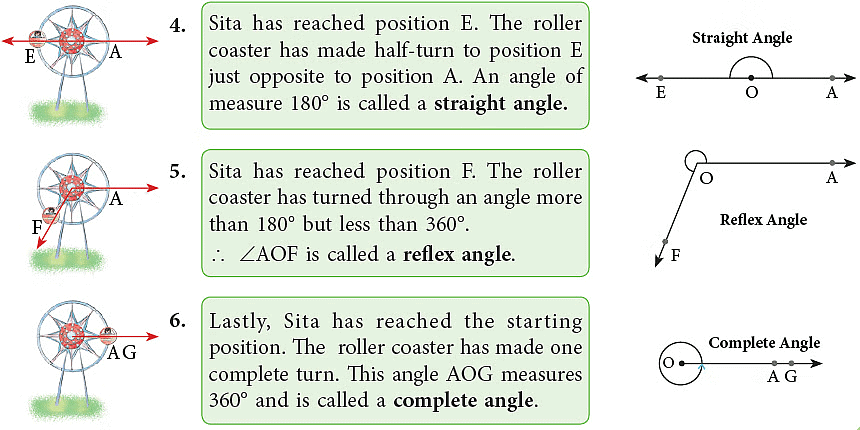
Equal Angles or Congruent Angles
When two angles have the same angle measure, we say that they are equal or congruent and write ∠ABC = ∠DEF.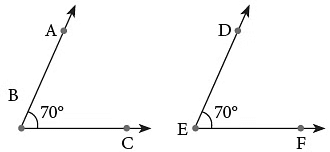 This means either angle can fit exactly over the other angle.
This means either angle can fit exactly over the other angle.
Open and Closed Shapes
1. Open Shapes
The shapes which do not begin and end at the same point are called open shapes.
Look at the following open shapes: 2. Closed Shapes
2. Closed Shapes
The shapes which begin and end at the same point are called closed shapes.
Observe the following closed shapes: (i) Simple Closed Figures
(i) Simple Closed Figures
Look at the following figures: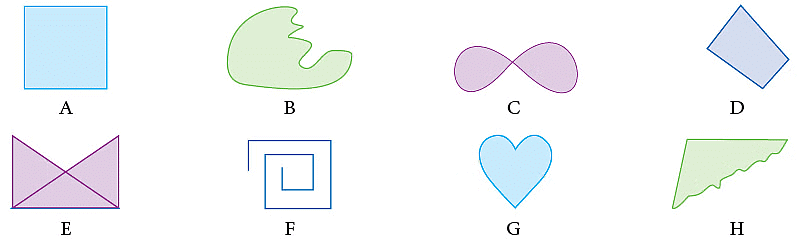
Which of the figures given above could you draw by starting at some point, never lifting your pencil from the paper and ending at the starting point?
Obviously, A, B, C, D, G and H. Such figures are called closed figures.
Out of these, which figures can you draw without having the figure crossed itself?
Ans: A, B, D, G and H. Such figures are called simple closed figures.
Tangrams
A tangram is a Chinese puzzle created using geometric shapes. You can make tangrams by cutting colourful sheets into five triangles, a square, and a parallelogram. These seven geometric shapes, called tans, can be combined in various ways to create different forms. When you arrange the pieces together, they can represent a wide range of shapes and illustrate many mathematical and geometric ideas. Tangram pieces are commonly used for solving puzzles. Interestingly, all seven pieces can be assembled to create a square. Check out the figure below that illustrates a seven-piece tangram.
 Tangram
Tangram
Why do we use Tangrams?
We use tangrams because they are like special building blocks that help us get better at solving problems and thinking smartly. Tangrams also make us good at understanding shapes, figuring out how things fit together, and being creative. They teach us important math ideas like matching shapes, making things symmetrical, finding the space inside shapes, and understanding the size around shapes. Kids who use tangrams can even do better in math tests, and there are lots of fun shapes and pictures, more than 6,500 of them, that we can make with tangrams!

Triangles
A triangle is a basic shape you see in many places. It is a simple closed figure made up of three straight line segments.
 Triangle we see in everyday life
Triangle we see in everyday life
So, in small-small things around us we see triangles. Triangle is a very common geometrical shape we use in day to day life.
A triangle has: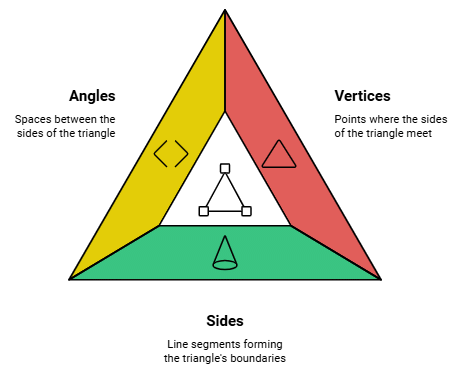
- Three Vertices: The points where the sides meet (like points A, B, and C in triangle ∆ABC).
- Three Sides: The line segments that form the triangle (AB, BC, and CA).
- Three Angles: The space between the sides (∠BAC, ∠ABC, and ∠BCA).

Triangles can be classified in two main ways:
Based on Sides:
- Scalene Triangle: All sides are different lengths.
- Isosceles Triangle: Two sides are of equal length.
- Equilateral Triangle: All three sides are equal in length.
Based on Angles:
- Acute-Angled Triangle: All angles are less than 90º
- Obtuse-Angled Triangle: One angle is greater than 90º
- Right-Angled Triangle: One angle is exactly 90º
So, in small-small things around us we see triangles. Triangle is a very common geometrical shape we use in day to day life.
Area and Perimeter of a Triangle
1. Perimeter of a Triangle
The perimeter of a triangle is the sum of all its three sides.
Perimeter = a+b+ c where a, b, and c are the three sides of the triangle.
2. Area of a Triangle
For triangles, you can find the area by multiplying the base and the height and then dividing by 2.
Area = (Base × Height) ÷ 2
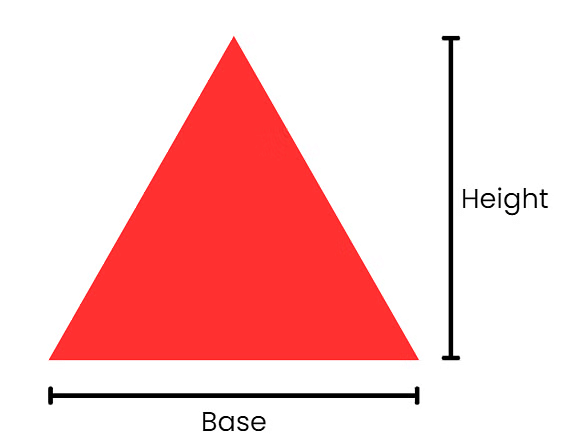
Example: If you have a triangle with a base of 4 units and a height of 6 units,
Area = (4 units × 6 units) ÷ 2 = 12 square units
Right-Angled Triangles and Pythagoras Theorem
Pythagoras theorem is related to the right-angled triangle. So, let us consider a right-angled triangle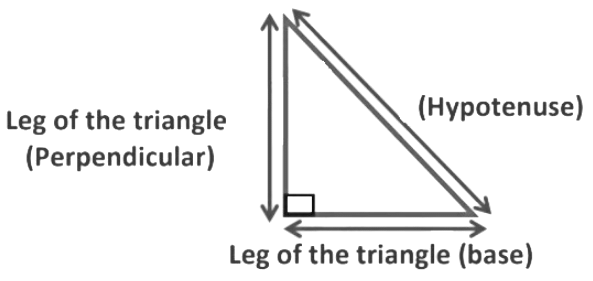
In a right-angled triangle, the side opposite to the right angle is called the hypotenuse, and the other two sides are known as legs of the right-angled triangle. So, perpendicular, base, and hypotenuse are the three sides of the right-angled triangle. Now, according to this theorem, if you have a right-angled triangle in which
a→ Leg of a triangle (Perpendicular side)
b→ Leg of a triangle (Base side)
c→ Hypotenuse
Then let’s try this if we draw a square on the perpendicular side that means each side of the square would be equal to a and the area of that square is equal to a2.
If we draw a square on the base side that means each side of the square would be equal to b and the area of that square is equal to b2.
In the same way, if we draw a square on hypotenuse side that means each side of the square would be equal to c and the area of that square is equal to c2.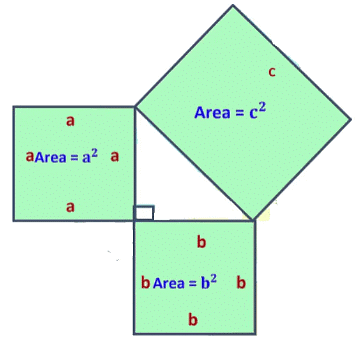 So, according to Pythagoras theorem,
So, according to Pythagoras theorem,
In a right-angled triangle, the square of the hypotenuse equals the sum of the square of its two sides.
∴ (Perpendicular)2 + (Base)2 = (Hypotenuse )2
∴ (a)2 + (b)2 = (c )2
This is called the Pythagoras theorem.
Circle
Look at the following objects. Which shape do all of the above objects remind you of?All these objects are in the shape of a circle.
Which shape do all of the above objects remind you of?All these objects are in the shape of a circle.
A circle is a simple closed curve.
Edurev Tips: A circle is not a polygon as it is not made up of straight lines.
Drawing a Circle
We can draw a circle using any one of these methods.
Method
- Take any circular object such as a coin, bottle cap, bangle, etc., and trace its outline. You will get the shape of a circle.
- Take a piece of thread and tie a pencil to one end of the thread. Fix the other end of the thread to the paper with a pin. Hold the thread tightly and rotate the pencil. The shape you get will be a circle.
- Using compasses which has a metal-pointed edge at A circle is not a polygon as it is not made up of straight lines. one end and a pencil holder on the other end.
To draw a circle using compasses:
Step 1: Fix the pencil to the compasses tightly. Adjust the pencil such that the needle and the pencil edge are at the same level.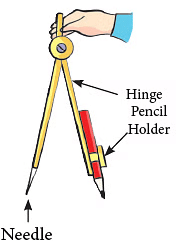 Step 2: Fix the needle of the compasses on the sheet of paper.
Step 2: Fix the needle of the compasses on the sheet of paper.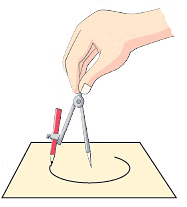 Step 3: Stretch the other arm of the compasses which is holding the pencil.
Step 3: Stretch the other arm of the compasses which is holding the pencil.
Step 4: Move the pencil around to draw a circle.
Parts of a Circle
- Centre
In the figure given alongside, O is the point where we put the metal end of the compasses to draw a circle. O is called the centre of the circle.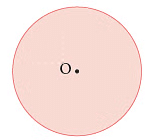 We name the circle with its centre.
We name the circle with its centre. - Radius
The line segment joining the centre of the circle to any point on the circle is called the radius of the circle.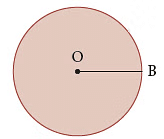 In the figure, line segment OB is the radius of the circle.
In the figure, line segment OB is the radius of the circle. - Chord
The line segment joining any two points on a circle is called a chord.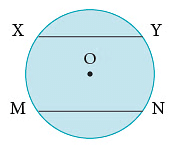 In the figure, XY and MN are the chords of the circle.
In the figure, XY and MN are the chords of the circle. - Diameter
A chord that passes through the centre is called a diameter of the circle.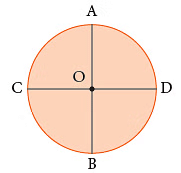 Here, AB and CD are the diameters of the circle O.
Here, AB and CD are the diameters of the circle O. - Circumference
The length of the boundary of a circle is called its circumference.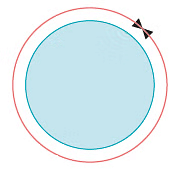
Relation between Radius and Diameter of a Circle
In the given figure, AB is the diameter of the circle. AO and OB are the two radii of the circle.
Measure OA, OB and AB. OA = ____ cm, OB = ____ cm, AB = ___ cm
You will find that AB = 2OA or 2OB = 2 × radius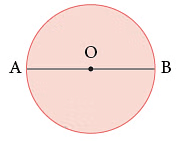
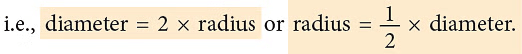
Interior and Exterior of a circle
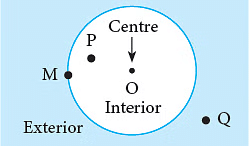
- The points O and P are in the interior of the circle.
- The point M is on the circle.
- The point Q lies to the exterior of the circle.
To Draw a Circle of Given Radius
You must use a pair of compasses to draw neat and accurate circles. Suppose, you have to draw a circle of radius 3 cm. You can do so by following these steps.
Step 1: With the help of your ruler, open the arms of your compasses to 3 cm length.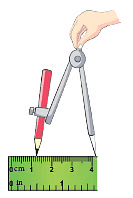 Step 2: Mark any point O on a piece of paper.
Step 2: Mark any point O on a piece of paper. Step 3: Place the steel end of the compasses on the dot marked O. Hold the head of the instrument between the thumb and the forefinger such that the pencil end of the compasses may touch the paper. Now, turn it completely round so that the pencil end traces a circle. You will get a circle of radius 3 cm, with centre O.
Step 3: Place the steel end of the compasses on the dot marked O. Hold the head of the instrument between the thumb and the forefinger such that the pencil end of the compasses may touch the paper. Now, turn it completely round so that the pencil end traces a circle. You will get a circle of radius 3 cm, with centre O.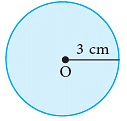
|
30 videos|210 docs|69 tests
|
FAQs on Notes: Geometry - Mathematics & Pedagogy Paper 1 for CTET & TET Exams - CTET & State TET
| 1. What are the different types of lines in geometry? |  |
| 2. How do you measure a line segment accurately? |  |
| 3. What is the difference between open and closed shapes? |  |
| 4. How do you find the area of a shape? |  |
| 5. What are tangrams, and how are they used in geometry? |  |





















