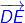Notes: Geometry | Mathematics & Pedagogy Paper 2 for CTET & TET Exams - CTET & State TET PDF Download
In this chapter, several important geometric terms are included which holds extreme importance in the later grades. The topics that are introduced not only will help students to build a foundation in geometry but will also help them to grasp the higher-level concepts in the later grades easily.

Introduction to Geometrical Ideas
The term ‘Geometry’ is the English equivalent of the Greek word "geo-metron"."Geo" means "Earth" and "metron" means "Measurement."
Therefore, geometry means the measurement of the earth.
In our daily life, we observe and use objects having different shapes:
The ruler, pencil, and pen are straight. Ball, bangle, coins, sun are round shaped.
Ball, bangle, coins, sun are round shaped.
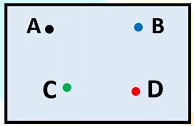
What is a Point?
- A point determines a specific location.
- They are denoted by any capital letter of the English Alphabet.
- It has no length, breadth or thickness.

We can draw a point with the tip of a sharp pencil, the tip of a compass, or the pointed end of a needle.
A point is usually represented by a small dot and is named by a single capital letter of the alphabet.
These points will be read as point A, point B and point C.
What is a Line Segment
A line segment corresponds to the shortest distance between two points.
The edge of a ruler and the edge of a box are examples of line segments.

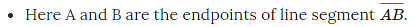
- A line segment has a fixed length.
- The line segment
 is same as its inverse.
is same as its inverse.
What is a Line?
- When a line segment is extended on both sides infinitely, then it is called a line. Here m is a line.
- It contains an infinite number of points on it.
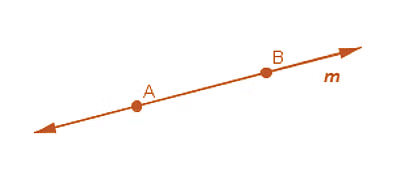
- A line is straight and extends indefinitely on both directions.
- A line segment
 extended on both sides and marked by arrows at the two ends represent a line, denoted by
extended on both sides and marked by arrows at the two ends represent a line, denoted by  or
or 
Example: Use the figure to name:
a) Five points
b) A line
c) Five line segments
a) Five points are O, B, C, D and E.
b) A line:c) Five line segments are ,
,
,
,
,
What are Intersecting and Parallel lines?
- If two lines have one common point, they are called intersecting line
- If there is a point P common to two lines
 and
and 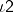 , then the twolines intersect at the point P and this point P is called the point of intersection of the given lines.
, then the twolines intersect at the point P and this point P is called the point of intersection of the given lines.
Parallel Lines
Two lines are said to be parallel if they are in the same plane and do not intersect each other.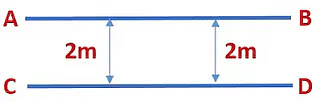


Perpendicular Lines
Two lines are said to be perpendicular when they intersect at 90 degree (right angle).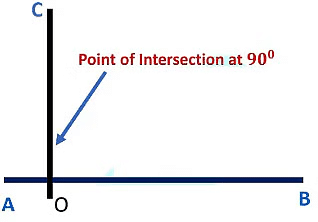

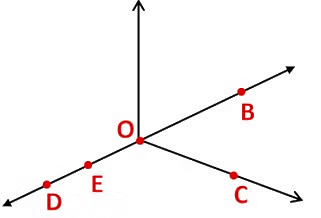
Example: Use the figure to name:
(a) Line containing point E.
(b) Line passing through A.
(c) Line on which O lies
(d) Two pairs of intersecting lines.
a) Line containing point E is
b) Line containing point A is
c) Line on which O lies
d) Two pairs of intersecting lines areand
,
and
What is a Ray?
Examples of the ray are: Beam of light from a lighthouse and sun rays.

Thus a line segment  extended endlessly in the direction fromA to B, is a ray denoted by
extended endlessly in the direction fromA to B, is a ray denoted by 

- The ray
 has one end (fixed) point called its initial point.
has one end (fixed) point called its initial point. - Rays
 and
and  are two different rays.
are two different rays. - Ray
 is a ray with initial point B and extends endlessly in thedirection from B to A.
is a ray with initial point B and extends endlessly in thedirection from B to A.
What is a curve?

- Curve can be anything which is drawn without lifting the pencil from the paper and without using a ruler.
- ‘Curve’ in everyday usage means “not straight”.
- In Mathematics, a curve can be a straight line called a straight curve.

Types of Curve
1. Simple Curve
If a curve does not cross itself, then it is called a simple curve.

The below shown curves are not Simple curves because they cross themselves.

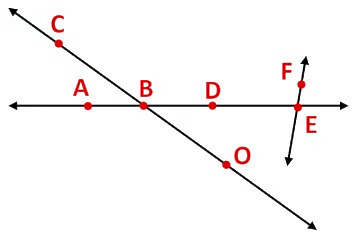
2. Open Curve
The curve which does not form a closed path is called an open curve.
In an open curve we can find at least one point where the curve begins or end.

3. Closed Curve
The curve which forms a closed path is called a closed curve.
In a closed curve we cannot find any point where the curve begins or ends.

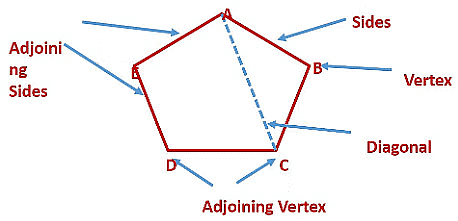
What is a Polygon?
A polygon is a closed figure formed of three or more line segments.
Examples of polygons are triangle, quadrilateral, pentagon and hexagon.
- Polygons are two dimensional.
- They are bounded by straight lines and the shapes is closed
- Minimum three line segments are required to make a closed figure, thus a triangle is a polygon with a minimum of three sides.

- The line segments forming a polygon are called its sides.
- The meeting point of a pair of sides is called a vertex.
- Any two sides with a common end point are called the adjacent sides of the polygon.
- The end points of the same side of a polygon are called the adjacent vertices.

Example: Classify the following curves as
(i) Open
(ii) Closed
Answer:
Example: Consider the given figure and answer the questions:
(a) Is it a curve?
(b) Is it closed?
(a) Yes, it is a curve because a curve is drawn without lifting the pencil from the paper and without using a ruler.
(b) Yes, it is closed because the curve forms a closed path.
Example: Illustrate, if possible, each one of the following with a rough diagram:
(a) A closed curve that is not a polygon.
(b) An open curve made up entirely of line segments.
(c) A polygon with two sides.
Answer:
a) A closed curve that is not a polygon.b) An open curve made up entirely of line segments.
c) A polygon with two sides cannot be drawn as minimum three
line segments are required to make a polygon.
Related Angles
1. Complementary Angles
- When the sum of the measures of two angles is 90°, the angles are called complementary angles.
- Whenever two angles are complementary, each angle is said to be the complement of the other angle.
Example: Clock
The hour-hand and the minute-hand of the clock form a pair of complementary angles.
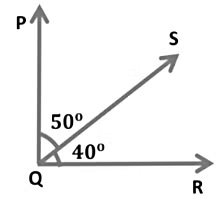 Complementary Angles
Complementary Angles
Here,
∠PQS + ∠SQR= 50° + 40° = 90°
In the above figure, we see that the sum of two angles is 90°.
Hence, ∠PQS and ∠SQR are complementary angles. And ∠PQS and ∠SQR are said to be complements of each other.
Example: Are the given angles complementary?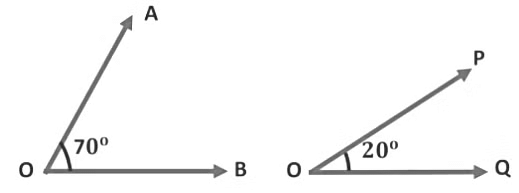 In the given figure,
In the given figure,
∠AOB = 70°and ∠POQ = 20°
∠AOB + ∠POQ = 70° + 20° = 90°
Therefore, ∠AOB and ∠POQ are complementary angles.
2. Supplementary Angles
- Two angles are said to be supplementary if the sum of their measure is equal to 180°.
- When two angles are supplementary, each angle is said to be the supplement of the other
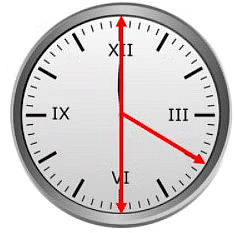 Clock
Clock
Example: Clock
- The two angles formed by the hands of the above clock are supplementary.
- The measure of two angles 120° and 60° are given and when we add up that angles we get 180°.
120° + 60° = 180°. - Hence, we can say that they are supplementary angles or supplements of each other.
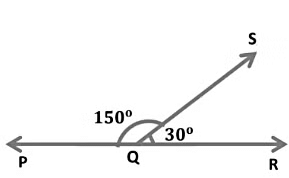 Supplementary Angle
Supplementary Angle
Here,
∠PQS + ∠SQR = 150° + 30° = 180°
In the above figure, we see that the sum of two angles is 180°.
Hence, ∠PQS and ∠SQR are supplementary angles, and ∠PQS and ∠SQR are said to be supplements of each other.
Example: The following ∠AOB and ∠POQ are supplementary angles or not?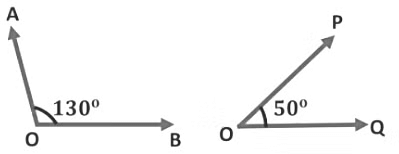 Supplementary Angle
Supplementary Angle
Sol: In the given figure,
∠AOB + ∠POQ = 130° + 50° = 180°
∠AOB + ∠POQ = 180°
∴ ∠AOB and ∠POQ are supplementary angles. Or
∠AOB and ∠POQ are said to be supplements of each other.
3. Adjacent Angles
These angles are such that:
(i) they have a common vertex.
(ii) they have a common arm.
(iii) the non-common arms are on either side of the common arm.
Such pairs of angles are called adjacent angles.
Note: Adjacent angles have a common vertex and a common arm but no common interior points.
Example: In the following figure angles marked with 1 and 2 are they adjacent? If not give a reason for that.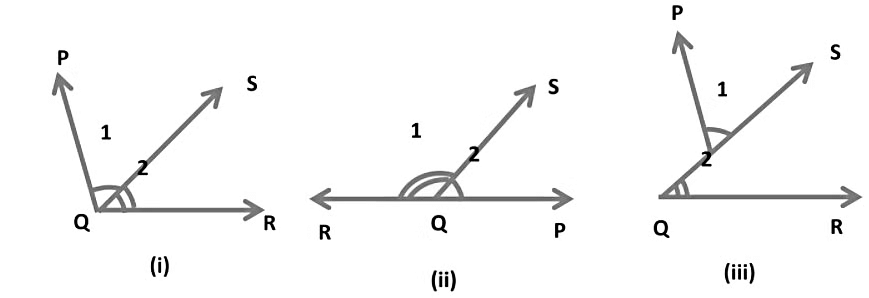 Adjacent Angle
Adjacent Angle
Solution:
In figure number (i)
(i) We see ∠PQS and ∠SQR have a common arm QS.
They have a common vertex Q.
They do not have a common interior point.
Hence, ∠PQS and ∠SQR are adjacent angles
In figure number (ii)
(ii) We see ∠RQS and ∠SQP have a common arm QS.
They have a common vertex Q.
They do not have a common interior point
Hence, ∠RQS and ∠SQP are adjacent angles
In figure number (iii)
(iii) We see ∠PTS and ∠SQR have a common arm QS.
They do not have a common vertex.
They do not have a common interior point.
The above figure does not satisfy all the conditions for being adjacent angles.
Hence, ∠PTS and ∠SQR are not adjacent angles.
Pairs of Lines
Pairs of Lines
1. Intersecting Lines
Two lines are said to be intersecting when they cross each other at one point only and the point at which they intersect is called the point of intersection.
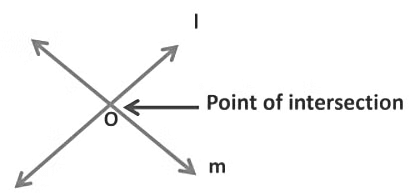 Here, two lines l and m intersect each other at point O, and point O is called the point of intersection.
Here, two lines l and m intersect each other at point O, and point O is called the point of intersection.
2. Transversal Line
A line that intersects two or more lines in a plane at distinct points is called a transversal line.
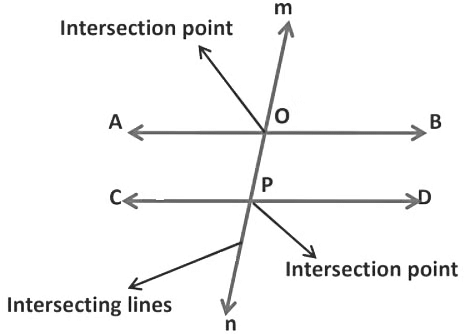
- Here, line mn intersects two lines AB and CD at two distinct points O and P respectively.
- Hence, line mn is called the transversal line and points O and P are called the points of intersection.
3. Angles made by a Transversal

Here, the two lines l and m are intersected by a transversal n at points O and P respectively. We see that four angles are formed at each point O and P, namely ∠1, ∠2, ∠3, ∠4, ∠5, ∠6, ∠7, and ∠8.


Example: In the figure given below, l || m and ∠1 = 53°. Find ∠6 and ∠7.
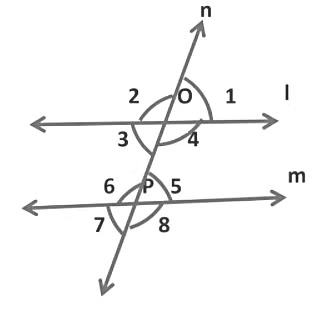
We have,
∠1 = ∠3 [Vertically opposite angles]
∠3 = ∠7 [Corresponding angles]
∴ ∠1 = ∠7
→ ∠7 = 53° ∵ ∠1 = 53° (Given)
∠6 + ∠7 = 180° [Linear pair]
∠6 + 53° = 180°
∠6 + 53° − 53° = 180° − 53°
∠6 = 127°
Thus, ∠6 = 127° and ∠7 = 53°
4. Transversal of Parallel Lines
If two lines lying in the same plane do not intersect when produced on either side, then such lines are said to be parallel to each other.

Here, lines l and m are parallel to each other, and transversal n intersects line l and m at point O and P respectively.
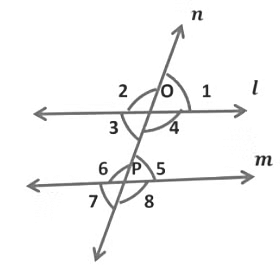
When the two parallel lines l and m are cut by a transversal n, then obtained the following relations:
(i) When a transversal intersects two parallel lines, then each pair of alternate interior angles are equal.
When line n intersects two parallel lines l and m, then we see that each pair of alternate interior angles is equal.
∴ ∠ 3 = ∠5, ∠4 = ∠6
(ii) When a transversal intersects two parallel lines, each pair of alternate exterior angles are equal.
When line n intersects two parallel lines l and m, then we see that each pair of alternate exterior angles is equal.
∴ ∠ 2 = ∠8, ∠1 = ∠7
(iii) When a transversal intersects two parallel lines, each pair of corresponding angles are equal.
When line n intersects two parallel lines l and m, then we see that each pair of corresponding angles is equal.
∴ ∠3 = ∠7, ∠2 = ∠6, ∠ 1 = ∠5, and ∠4 = ∠8
(iv) When a transversal intersects two parallel lines, then each pair of interior angles on the same side of the transversal are supplementary
When line n intersects two parallel lines l and m, then we see that each pair of interior angles on the same side of the transversal are supplementary.
In the above figure, ∠ 3 = ∠4 .....Linear pair of angles
We know sum of the linear pair of angles is 180° ∴ ∠ 3 + ∠4 = 180°
But, ∠4 = ∠6 ...Pair of alternate interior angles Therefore, we can say that ∴ ∠ 3 + ∠6 = 180°
Similarly, ∠4 + ∠5 = 180°
Example: In the given figure l || m, ∠1 = 55°. Find ∠5, ∠6, and ∠7.
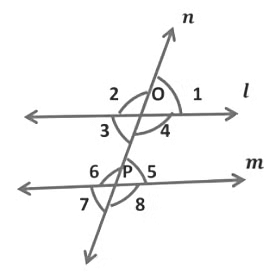
We have,
∠ 1 = ∠5 .....Corresponding angles
∴ ∠ 5 = 55° [∵ ∠1 = 55°]
∠5 = ∠7 .....Vertically opposite angles
∴ ∠7 = 55° [∵ ∠5 = 55°]
Now,
∠ 6 + ∠7 = 180°.....Linear pair of angles
∠ 6 + 55° = 180°
∠ 6 + 55° − 55° = 180° − 55°
∠ 6 = 180° − 55°
∠ 6 = 125°
Thus, ∠ 5 = 55°, ∠ 6 = 125°and ∠7 = 55°
Checking for Parallel Lines
Some special pairs of angles can be used to test if the lines are parallel or not.
(i) When a transversal intersects two parallel lines, such that if any pair of corresponding angles are equal, then the lines are parallel.
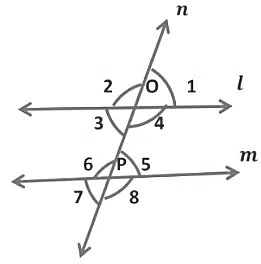
In the given figure, transversal n intersects two lines l and m in such a way that,
∠3 = ∠7, ∠2 = ∠6, ∠ 1 = ∠5, and ∠4 = ∠8 ...(Pairs of corresponding angles are equal)
Hence, we can say that lines are parallel.
(ii) When a transversal intersects two parallel lines, such that if any pair of alternate interior angles are equal, the lines have to be parallel.
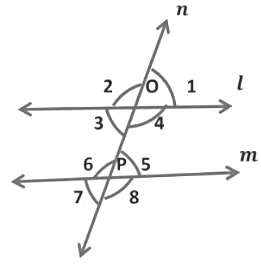
In the given figure, transversal n intersects two lines l and m in such a way that,
∠ 3 = ∠5, ∠4 = ∠6 ... (Alternate interior angles are equal)
Hence, we can say that lines are parallel.
(iii) When transversal intersects two parallel lines, such that if any pair of alternate exterior angles are equal, the lines have to be parallel.

In the given figure, transversal n intersects two lines l and m in such a way that,
∠1 = ∠7, ∠2 = ∠8 ... (Alternate exterior angles are equal)
Hence, we can say that lines are parallel.
(v) When transversal intersects two parallel lines, such that if any pair of interior angles on the same side of the transversal are supplementary, the lines have to be parallel.
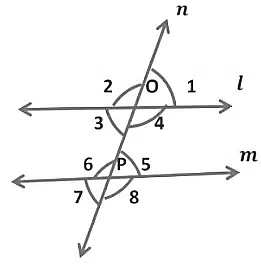
In the given figure, transversal n intersects two lines l and m in such a way that, ∠ 3, ∠6 and ∠4, ∠5 ...Pairs of co-interior angles or angles on the same sides of the transversal
Hence,
∠ 3 + ∠6 = 180° and
∠4 + ∠5 = 180°
Hence, we can say that lines are parallel.
Example: Find whether AB || CD.
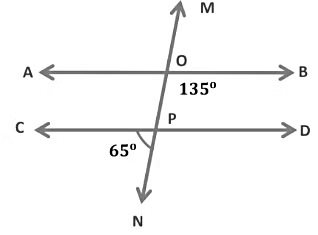
In the given figure,
∠CPN = ∠OPD = 65°...Vertically opposite angles
∠BOP + ∠OPD = 180°
Thus, the sum of co-interior angle is 180°
Hence,
135° + ∠OPD = 180°
∠OPD = 180° − 135°
∠OPD = 45°
Therefore, AB || CD
What is a Triangle?
A triangle is a three-sided polygon. It is the polygon with the least number of sides. It is denoted by the symbol ∆.
We see many triangle shaped objects in our daily life.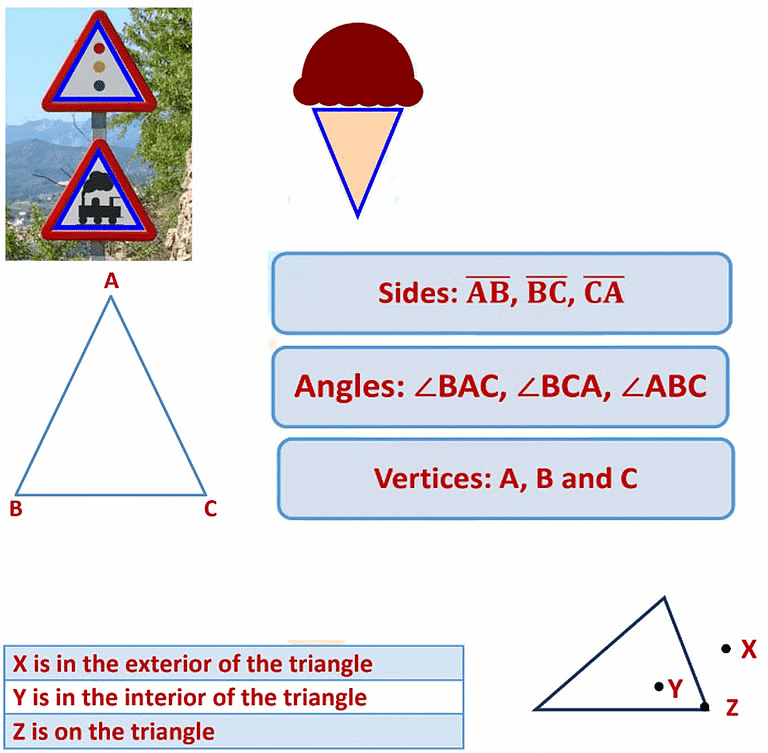 Example:
Example:
Draw a rough sketch of a triangle ABC. Mark a point P in its interior and a point Q in its exterior. Is the point A in its exterior or in its interior?
Point A is not in the interior or exterior of ∆ ABC as it is a vertex (a point where two line segments meet).
What is a Quadrilateral?
A four sided polygon is a quadrilateral. It has 4 sides and 4 angles.

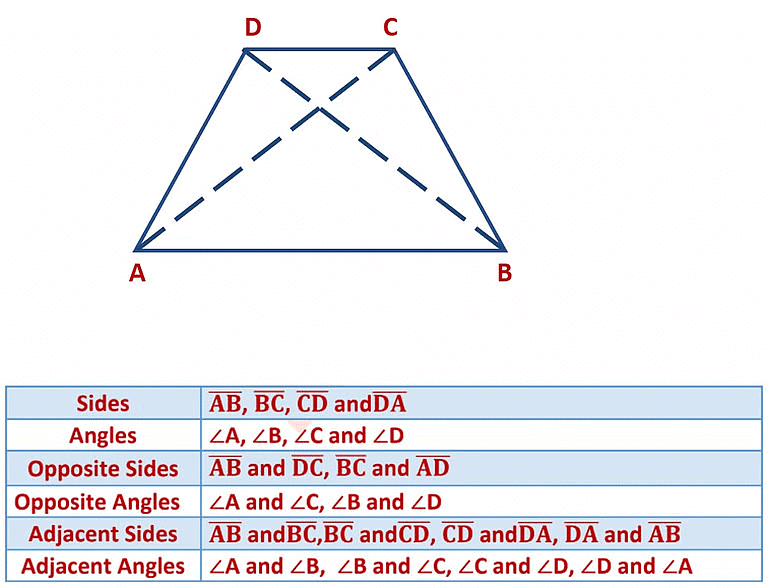
Example: Draw a rough sketch of a quadrilateral PQRS.
Draw its diagonals.
Name them.
Is the meeting point of the diagonals in the interior or exterior of the quadrilateral?
The two diagonals are PR and QS. Diagonal PR and diagonal QS meet at point T which is in the interior of the quadrilateral PQRS.
What is a Circle?
A circle is a simple closed curve which is not a polygon. We see many things that are round, a clock, a bangle, coin.
Parts of a circle
Here is a circle with center O. A, P, B, M are points on the circle.
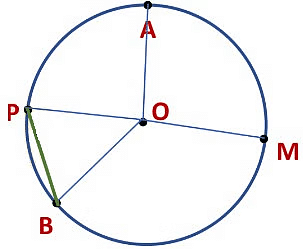

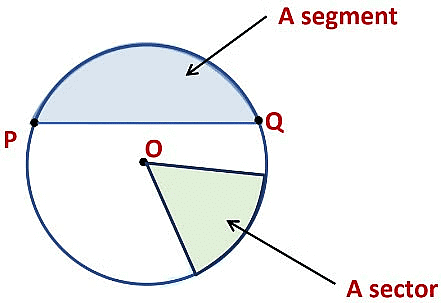

Example: From the figure, identify:
(a) The center of circle
(b) Three radii
(c) A diameter
(d) A chord
(e) Two points in the interior
(f) A point in the exterior
(g) A sector
(h) A segment

(a) O is the center of the circle.
(d) ED is a chord
(b) OA, OB and OC are the three radii
(c) AC is the diameter of the circle
(e) O and P are the two points in the interior.
(f) Q is the point in the exterior
(g) OAB (shaded portion) is a sector
(h) ED (shaded portion) is a segment
|
82 videos|273 docs|69 tests
|
FAQs on Notes: Geometry - Mathematics & Pedagogy Paper 2 for CTET & TET Exams - CTET & State TET
| 1. What is the difference between a point, a line segment, and a line? |  |
| 2. How do you identify intersecting and parallel lines? |  |
| 3. What is a ray in geometry? |  |
| 4. Can a curve be a straight line in geometry? |  |
| 5. How many sides does a polygon have? |  |