Kinematics of Particle | Civil Engineering Optional Notes for UPSC PDF Download
Defining the Kinematics of Particles
The kinematics of particles can be considered the 'grammar' of motion. It provides a framework for describing changes in an object's motion in terms of displacement, velocity, and acceleration. Let's break down these attributes:- Displacement: This refers to the overall change in position of the particle. It is a vector quantity that specifies both the distance and direction from the initial position to the final position.
- Velocity: This is the rate of change of the particle's displacement with time. It is also a vector quantity, describing how fast and in what direction the particle is moving.
- Acceleration: This describes the rate of change of velocity with time. It indicates how quickly the particle's velocity is changing, both in magnitude and direction.
In summary, 'kinematics' is a way to describe how things move, while 'particles' can refer to anything from tiny atoms to huge stars, as long as they are treated as point masses with no size or shape.
Breaking Down the Kinematics of Particles Formula
Here, you'll find the most common formulae in the world of kinematics, and it's essential to understand their meaning and use. In kinematics, you often have to compute the final velocity (
Interpretation of the Kinematics of Particles Formula
Example: Imagine a car speeding up from rest. Initially, the car's velocity (
) is 0, and let's say it accelerates ( ) at a rate of 2 m/s² for 3 seconds ( ). The car's final velocity ( ) can then be found with , equivalent to m/s.
Delving into Real-Life Kinematics of Particles Examples
There's no better way to understand the concepts of kinematics than by delving into real-life examples. For one to truly grasp the complex subject that is the kinematics of particles, it helps to apply what you know to situations you encounter in your everyday life or field of study. Let's explore two distinct categories - everyday scenarios and engineering applications.Engaging with Kinematics of Particles Examples in Daily Life
Even as you go about your daily routines, unsuspectingly, you're surrounded by practical applications of kinematics. It might be a bit hard initially to fathom how the motion of particles applies to your everyday life, but the truth is, when you boil down complex systems to their simplest elements - particles, kinematics relentlessly governs their behaviour. Let's dissect a few examples:Example 1. Throwing a Ball: Whenever you toss a ball into the air, it follows a parabolic trajectory. The motion of the ball can be predicted using kinematics. As soon as the ball leaves your hand, it has an initial velocity (
) and is subject to acceleration due to gravity( ). By the time it reaches its highest point, its final velocity ( ) is 0. Using the formulas or , you can calculate the height it reaches and how long it stays in the air.
Example 2. Driving a Car: Have you ever thought about how the kinematics of particles is in play when you're driving? Every time you accelerate or decelerate in your car, you're making use of kinematics concepts to control your velocity and positioning. For instance, if you want to overtake someone, you need to calculate if you have enough distance to accelerate and then decelerate back to cruising speed again. The comprehensive understanding of kinematics here determines the safety of your manoeuvre.
Analysing Kinematics of Particles Examples in Engineering
Engineering is quintessentially an applied field, where almost every aspect is underpinned by the governing principles of physics. The kinematics of particles is no exception and is vigorously employed in various realms of engineering. It noticeably enables engineers to predict particle motion, optimizing designing and functionality. Let's assess some engineering examples with kinematics:Example 1. Robotic Arms: The kinematics of particles is integral to the design and functioning of robotic arms. Each point in a robotic arm can be considered a particle, and its motion in the three-dimensional space can be calculated using kinematic equations. Engineers use kinematics to determine how to articulate the multiple joints in a robotic arm so it can reach a specified location with the desired orientation.
Example 2. High-Speed Trains: Kinematics is instrumental in the design and control of high-speed trains. One of the primary factors is the determination of the trains' rates of acceleration and deceleration. This can help in calculating the minimum time and distance needed to reach a certain speed or stop the train from a particular speed. Incorporating such calculations into the design phase maximizes safety and efficiency.
Applications of Kinematics of Particles in Various Fields
From the microscopic realm of atoms and molecules to the vast scale of planetary orbits, the kinematics of particles has profound applications permeating various sectors:Automobile Industry: Engineers consider various kinematic factors when designing vehicles. For example:
- Speedometer: Displays the vehicle's real-time velocity.
- Odometer: Provides the total displacement traveled by the vehicle.
Space and Astronomy:
- Space Exploration: Spacecraft routes are planned using kinematic principles to predict planetary motions, helping scientists determine when a planet will be in a specific location.
Sports:
- Performance Improvement: Sports professionals and coaches use kinematics to enhance performance and technique. For instance, a golfer might analyze their stroke in terms of velocity and displacement to improve shot accuracy and distance.
Medical Field:
- Medical Imaging Technologies: Kinematics is fundamental in the functioning and application of technologies such as magnetic resonance imaging (MRI) and computed tomography (CT).
In essence, the applications of the kinematics of particles span various fields, underpinning numerous everyday phenomena and high-precision engineering systems, subtly yet significantly influencing lives.
The Impact of Kinematics of Particles Applications in Modern Technology
The kinematics of particles has profoundly transformed various aspects of modern technology, serving as a pivotal driver behind numerous technological advancements and contributing significantly to the development of increasingly efficient mechanical systems and devices.- Industrial Automation: Modern industries heavily rely on automation to enhance efficiency and minimize human errors. Automated machines follow the laws of kinematic equations to perform precise and swift movements. For example, in a factory setting, automated robotic arms use kinematic principles to accurately position objects from one point to another, optimizing production processes and ensuring high precision.
- Virtual Reality: The rise of virtual reality (VR) in gaming and simulations has advanced alongside developments in kinematics. By tracking the real-time motion of point masses or 'particles,' VR technologies can accurately render movements in the virtual world, providing users with a highly immersive experience. This application of kinematics allows for realistic and responsive interactions within virtual environments.
In summary, the applications of the kinematics of particles have significantly influenced modern technology, driving innovations and improving the functionality and efficiency of various systems in industrial automation and virtual reality.
Future Scenarios of Kinematics of Particles Applications
The current technological trajectory suggests that the principles of kinematics will continue to play a vital role in future technological developments. Here’s a brief look at potential future scenarios:Autonomous Vehicles:
As autonomous vehicles gain more traction, their navigation systems will continue to incorporate complex kinematic principles. Understanding the motion of the vehicle and predicting its future positions based on current velocity and acceleration will be essential for safe and efficient navigation. This will involve:
- Real-Time Data Processing: Continuous analysis of the vehicle's motion and surroundings to make instantaneous decisions.
- Collision Avoidance: Using predictive models to prevent accidents by anticipating potential hazards.
- Optimal Routing: Determining the most efficient paths by calculating precise movement trajectories.
Aerospace Engineering
With the increasing interest in interplanetary missions and space exploration, the role of kinematics will become even more crucial. Foreseeing the motion path of space vehicles and calculating planetary positions will aid in mission planning and execution. This will include:
- Trajectory Prediction: Accurate calculations to ensure spacecraft reach their destinations.
- Planetary Exploration: Precise landing and navigation on other celestial bodies.
- Search for Extraterrestrial Life: Planning and executing missions to potential habitats beyond Earth.
Defining Kinematics and Kinetics of Particles
The subjects of kinematics and kinetics form the two main pillars of understanding particle movement. Their concepts underpin the study of bodies in motion, from celestial mechanics to modern-day robotics.Kinematics: Kinematics is the study of the geometry of motion. It deals with the description of motion without concerning the forces causing it. Parameters such as displacement, velocity, and acceleration are used to describe the state of a moving particle. Main equations of kinematics include those of uniform acceleration, where displacement

Kinetics: Kinetics, on the other hand, is the study of the action of forces on bodies. It delves into why motion occurs by inspecting the forces causing it. Kinetics enunciates the cause-and-effect relationship between the forces acting upon a body and the changes in its motion due to these forces. The primary equation in kinetics is Newton's second law of motion, given by:
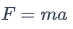
Here, F represents the applied force, m stands for the mass of the body, and a is the resulting acceleration.
Contrast between Kinematics and Kinetics of Particles
While both kinematics and kinetics deal with aspects of motion, they differentiate in their approach towards understanding and explaining movement. In essence, kinematics describes the motion of bodies, whereas kinetics unravels why these bodies move the way they do.
Focus
Kinematics: Focuses mostly on the study of motion in terms of quantities such as displacement, velocity, and acceleration. These quantities are described without any reference to the forces that result in motion.
Kinetics: Concerns itself with the forces causing motion, such as gravitational pull, electromagnetic push, or applied forces in mechanical systems. It delves into the underlying reasons for the observed motion.
Methodology
Kinematics: Utilizes directly observable and measurable quantities, such as distance and time, to describe motion.
Kinetics: Requires a deeper understanding of physical interactions involving forces. Forces cannot be directly observed but are inferred through their effects on velocity and acceleration.
Applications
Kinematics: Finds significant use in areas requiring the description of motion alone, such as animation and robotics.
Kinetics: Extensively applied in fields involving the study of forces and energy, including dynamics, system design, and mechanical engineering.
Through analyzing these contrasting aspects, it becomes evident how kinematics and kinetics, while both tackling particle motion, provide different perspectives: an understanding of what motion is occurring versus why it's happening.
|
350 videos|464 docs|2 tests
|
|
350 videos|464 docs|2 tests
|

|
Explore Courses for UPSC exam
|

|
















