Mechanical Properties of Fluids: Capillarity | Physics for JEE Main & Advanced PDF Download
| Table of contents |

|
| Practical Applications of Capillarity |

|
| Capillary Rise (Height of a Liquid in a Capillary Tube) |

|
| Discussion |

|
| Capillary Rise in a Tube of Insufficient Length |

|
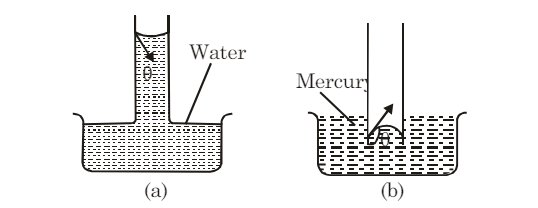
A glass tube with a very fine bore throughout its length is called a capillary tube. When a capillary tube is dipped in water, the water wets the inner side of the tube and rises inside it, as shown in figure (a). Conversely, if the same capillary tube is dipped in mercury, the mercury is depressed, as shown in figure (b). This phenomenon, where liquids rise or fall in a capillary tube, is known as capillarity.
Practical Applications of Capillarity
- Oil in a Lamp: The oil rises in the wick by capillary action.
- Pen Nib: The tip of the nib is split to form a narrow capillary, allowing ink to rise continuously.
- Sap in Trees: Sap and water rise to the top of tree leaves by capillary action.
- Wet Towels: If one end of a towel is dipped in a bucket of water and the other end hangs outside, the towel becomes wet throughout due to capillary action.
- Blotting Paper: Ink is absorbed by blotting paper due to capillary action.
- Soil Moisture: Sandy soil is drier than clay because the capillaries between sand particles are too large to draw water up effectively.
- Agricultural Practices: Moisture rises in soil capillaries to the surface, where it evaporates. Ploughing and leveling fields break these capillaries to preserve soil moisture.
- Porous Bricks: Bricks are porous and act like capillaries.
Capillary Rise (Height of a Liquid in a Capillary Tube)
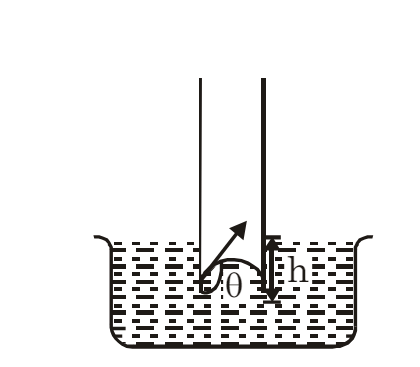
Consider a liquid that wets the wall of the tube, forming a concave meniscus as shown in the figure. Let a capillary tube of radius r be dipped in a liquid with surface tension T and density ρ. Let h be the height the liquid rises in the tube. The excess pressure (p−pa) is given by:
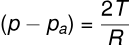
where R is the radius of the meniscus. This excess pressure causes the liquid to rise in the capillary tube until it balances the hydrostatic pressure hρg. Thus, in equilibrium:
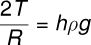

From triangle DOAC:

Therefore,
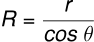
and
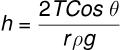
This expression is called the Ascent Formula.
Discussion
(i) Wetting Liquids: For liquids that wet the glass tube, θ<90∘ and cosθ is positive, hence h is positive. These liquids rise in the capillary tube. Examples include water, milk, kerosene oil, and petrol.
(ii) Non-wetting Liquids: For liquids that do not wet the glass tube, θ>90∘ and cosθ is negative, hence h is negative. These liquids are depressed in the capillary tube, such as mercury.
(iii) Jurin’s Law: Since and g are constants, . Thus, the liquid rises more in a narrow tube and less in a wider tube.
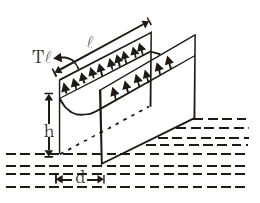
(iv) Parallel Plates in Water: If two parallel plates with spacing d are placed in a water reservoir, the height of the rise h is:

(v) Concentric Tubes: If two concentric tubes of radii r1 and r2 (inner one solid) are placed in water, the height of the rise h is:
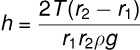
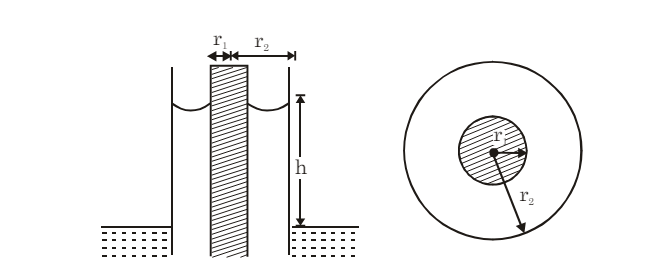
(vi) Considering Liquid Weight in Meniscus:
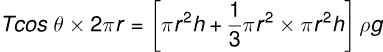
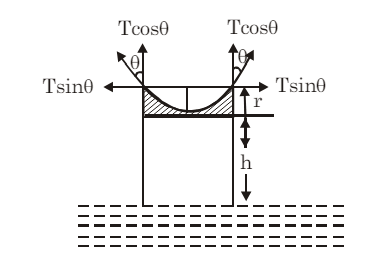
(vii) Meniscus Shape in Capillary Tube: When the capillary tube is vertical, the upper meniscus is concave, and the pressure due to surface tension is directed vertically upward.
(a) If , the lower meniscus is concave downward.
(b) If , the lower meniscus is convex upward. (c) If , the lower surface will be flat.
(viii) Liquid Between Two Plates: When a small drop of water is placed between two glass plates, it forms a thin film concave outward along its boundary.
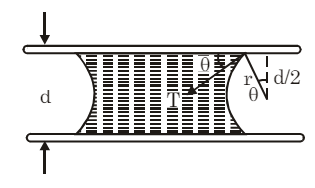
The pressure inside the film is:
If (water and glass), the upper plate is pressed downward by:

Capillary Rise in a Tube of Insufficient Length
The height to which a liquid rises in a capillary tube of radius r is given by the equation:
where:
- is the surface tension,
- is the contact angle,
- is the density,
- is the acceleration due to gravity.
When a capillary tube is cut and its length is less than the calculated height h (let's denote this shorter length as h′), the liquid rises to the top of the tube and spreads out, increasing the radius R′ of the liquid meniscus. The liquid does not overflow because the product hR remains constant. Therefore, constant.
Given that , it follows that , which implies , leading to , and hence .
Example Problem
Problem Statement: A 5 cm long capillary tube with an internal diameter of 0.1 mm, open at both ends, is dipped in water with a surface tension of 75 dyne/cm. Determine:
- Whether water will rise halfway in the capillary.
- Whether water will rise to the upper end of the capillary.
- Whether water will overflow out of the upper end of the capillary.
Solution: Given:
- Surface tension of water, dyne/cm,
- Radius of the capillary tube, r=20.1 mm = 0.05 mm = 0.005 cm,
- Density of water, g/cm³,
- Contact angle, .
Using the formula for capillary rise height h:

cm
Since the capillary tube length is 5 cm:
- Water will not rise halfway in the capillary: h is greater than '/ 2.
- Water will rise to the upper end of the capillary: The tube is insufficiently long, so the water rises to its upper end.
- Water will not overflow: It will rise only to the tube's upper end.
The radius of curvature of the liquid meniscus adjusts such that R′h′=Rh:
R' = 0.0306 cm
Applications of Surface Tension
- Detergents and Waterproofing: Detergents decrease the contact angle, increasing wettability. Waterproofing agents increase the contact angle, making fabrics water-repellent.
- Antiseptics: Low surface tension prevents droplet formation, allowing antiseptics to spread over wounds. Similarly, lubricating oils and paints have low surface tension to cover large areas effectively.
- Oil Spreading on Water: Oil spreads over water because its surface tension is lower than that of cold water.
- Calming Rough Seas: Oil can calm rough seas by reducing the surface tension of water.
Effect of Temperature and Impurities on Surface Tension
Temperature: Surface tension decreases with an increase in temperature. According to Ferguson's formula:
where To is the surface tension at 0°C,
is the absolute temperature,
θc is the critical temperature, and is a constant (mean value 1.21).
Surface tension becomes zero at the critical temperature.
Impurities: The addition of impurities affects surface tension. Highly soluble substances like NaCl increase water's surface tension, while sparingly soluble substances like phenol and soap decrease it.
|
289 videos|635 docs|179 tests
|
FAQs on Mechanical Properties of Fluids: Capillarity - Physics for JEE Main & Advanced
| 1. How does capillarity affect the height of a liquid in a capillary tube? |  |
| 2. What factors affect the capillary rise in a tube of insufficient length? |  |
| 3. How is capillarity related to the mechanical properties of fluids? |  |
| 4. Can capillarity be used in practical applications beyond capillary rise in tubes? |  |
| 5. How can the concept of capillarity be tested or demonstrated in a laboratory setting? |  |

|
Explore Courses for JEE exam
|

|

















