Notes: Relations and Functions | Mathematics (Maths) for JEE Main & Advanced PDF Download
Relations
Given any two non-empty sets A and B, a relation R from A to B is a subset of the Cartesian product A × B and is derived by describing a relationship between the first element (say x) and the other element (say y) of the ordered pairs in A & B.
Further, if (x, y) ∈ R, then we say that x is related to y and write this relation as x R y. Hence, R = {(x, y); x ∈ A, y ∈ B, x R y}.
Note: Ordered pairs means (x, y) and (y, x) are two different pairs.
Example: If R is a relation between two sets A = {1,2,3} and B = {1,4,9} defined as "square root of ". Here, 1R1, 2R4, 3R9
Then, R = {(1, 1), (2, 4), (3, 9)}.
| x | y |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
[Intext Question]
Representation of a Relation
1. Roster form: In this form, a relation is represented by the set of all ordered pairs belonging to R. If R is a relation from set A = {1,2,3,4} to set B = {1,4,9,16,25} such that the second elements are square of the first elements. So, R can be written in roster form as
R = {(1,1),(2,4),(3,9),(4,16)}
2. Set-builder form: In this form the relation R from set A to B is as
R = {(x,y): x∈A, y∈B; The rule which asociates x and y}
Example: R = {(1,1),(2,4),(3,9),(4,16)} can be written in set-builder form as
R = {(x,y): x∈A, y∈B; y=x2}, where A = {1,2,3,4}, B = {1,4,9,16}.
3. Visual Representation (Arrow Diagram)
In this form of representation, we draw arrows from first element to the second element for all ordered pairs belonging to R.
Example: Let R = {(1,5),(1,6),(2,5),(3,5)} from set A = {1,2,3} to set B = {5,6}
It can be represented by the following arrow diagram.
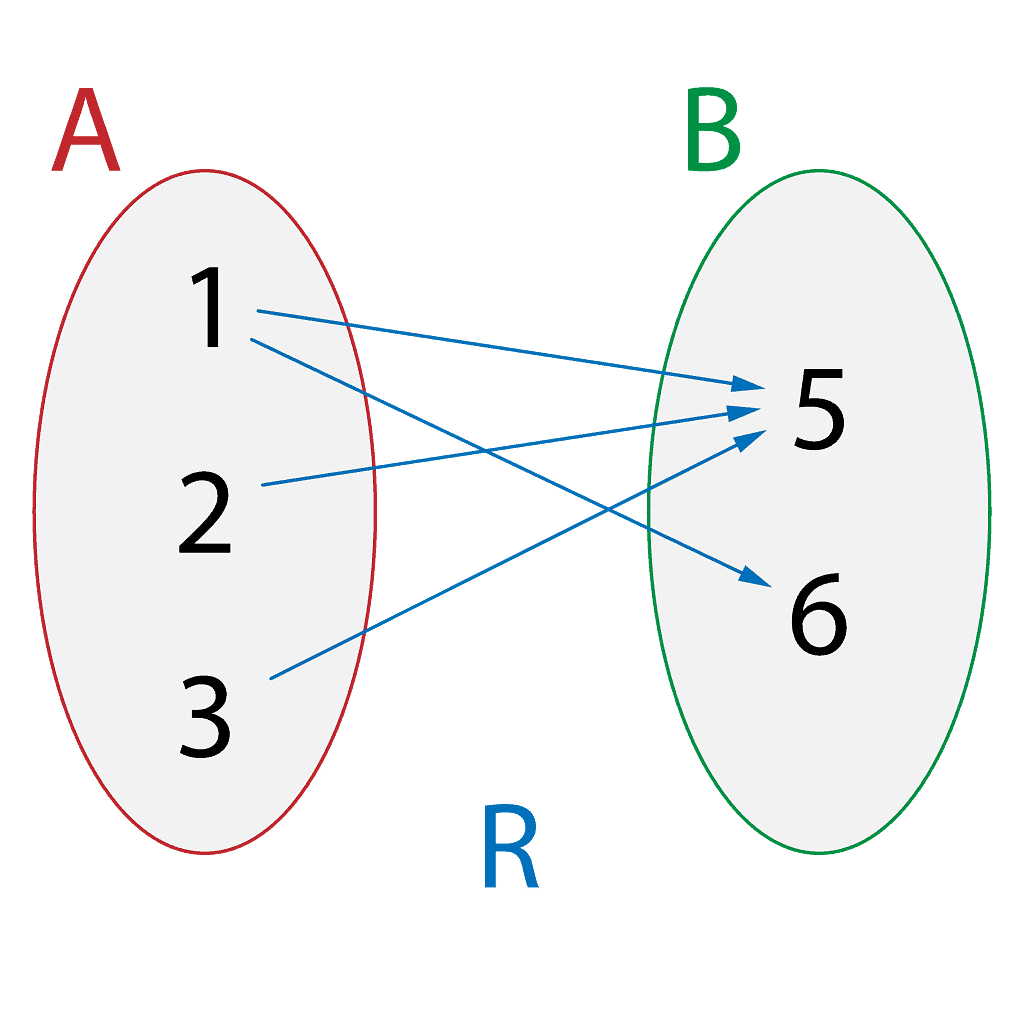
Domain and Range of a Relation
1. Domain of a Relation
Let R be a relation from A to B. The domain of relation R is the set of all those elements a ∈ A such that (a,b) ∈ R for some b ∈ B.
Thus domain of R = {a ∈ A: (a,b) ∈ R for some b ∈ B}
= set of first elements of all the ordered pairs belonging to R
2. Range of a Relation
Let R be a relation from A to B. The range of R is the set of all those elements b ∈ B such that (a,b) ∈ R for some a ∈ A.
Thus range of R = {b ∈ B: (a,b) ∈ R for some a ∈ A}
= set of second elements of all the ordered pairs belonging to R.
3. Co-domain of a Relation
If R be a relation from A to B, then B is called the co-domain of relation R.
Clearly range of a relation ⊆ co-domain.
[Intext Question]
Total Number of Relations
For two non-empty finite sets A and B. If the number of elements in A is h i.e., n(A) = h & that of B is k i.e. n(B) = k, then the number of ordered pair in the Cartesian product will be n(A × B) = hk. The total number of relations is 2hk.
Types of Relations
1. Empty Relation
If no element of set X is related or mapped to any element of X, then the relation R in A is an empty relation, i.e, R = Φ. Think of an example of set A consisting of only 100 hens in a poultry farm. Is there any possibility of finding a relation R of getting any elephant in the farm? No! R is a void or empty relation since there are only 100 hens and no elephant.
2. Universal Relation
A relation R in a set, say A is a universal relation if each element of A is related to every element of A, i.e., R = A × A. Also called Full relation. Suppose A is a set of all - natural numbers and B is a set of all whole numbers. The relation between A and B is universal as every element of A is in set B. Empty relation and Universal relation are sometimes called trivial relation.
3. Identity Relation
In Identity relation, every element of set A is related to itself only. I = {(a, a), ∈ A}.
Example: If we throw two dice, we get 36 possible outcomes, (1, 1), (1, 2), … , (6, 6). If we define a relation as R: {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)}, it is an identity relation.
4. Inverse Relation
Let R be a relation from set A to set B i.e., R ⊆ A × B. The relation R-1 is said to be an Inverse relation if R-1 from set B to A is denoted by R-1 = {(b, a): (a, b) ∈ R}. Considering the case of throwing of two dice if R = {(1, 2), (2, 3)}, R-1 = {(2, 1), (3, 2)}. Here, the domain of R is the range of R-1 and vice-versa.
5. Reflexive Relation
If every element of set A maps to itself, the relation is Reflexive Relation. For every a ∈ A, (a, a) ∈ R.
Example: Let A = {1, 2, 3}
Then R1 = {(1, 1), (2, 2), (3, 3)}
R2 = {(1, 1), (2, 2), (3, 3), (1, 2)}
R3 = {(1, 1), (2, 2), (1, 2)}
Clearly ,R1, R2 both are reflexive relation, but R3 is not reflexive relation because (3, 3) ∉ R3
Note: Every identity relation is reflexive relation,but every reflexive relation is not identity relation.
6. Symmetric Relation
A relation R on a set A is said to be symmetric if (a, b) ∈ R then (b, a) ∈ R, a & b ∈ A.
Example: Let A = {1, 2, 3}
Then R1 = {(1, 1), (2, 2), (3, 3)}
R2 = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 1)}
R3 = {(1, 1), (2, 2), (1, 2)}
Clearly, R1, R2 both are symmetric relation, but R3 is not symmetric relation because (1, 2) ∈ R3 , but (2, 1) ∉ R3
Note: A relation is called symmetric if R = R-1.
7. Transitive Relation
A relation in a set A is transitive if, (a, b) ∈ R, (b, c) ∈ R, then (a, c) ∈ R, a, b, c ∈ A
Example: Let A = {1, 2, 3}
Then R1 = {(1, 1), (2, 2), (3, 3)}
R2 = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 1)}
R3 = {(1, 1), (2, 2), (1, 2), (2, 3)}
Clearly ,R1, R2 both are transitive relation, but R3 is not transitive relation because(1, 2) & (2, 3) ∈ R3, but (1, 3) ∉ R3
Note:
Every empty relation defined on a non empty set is always symmetric and transitive but not reflexive.
Every universal set defined on non empty set is always reflexive, symmetric and transitive.
8. Equivalence Relation
A relation is said to be equivalence if and only if it is Reflexive, Symmetric, and Transitive.
Example: If we throw two dices A & B and note down all the possible outcome.
Define a relation R= {(a, b): a ∈ A, b ∈ B}, we find that {(1, 1), (2, 2), …, (6, 6) ∈ R} (reflexive). If {(a, b) = (1, 2) ∈ R} then, {(b, a) = (2, 1) ∈ R} (symmetry). If {(a, b) = (1, 2) ∈ R} and {(b, c) = (2, 3) ∈ R} then {(a, c) = (1, 3) ∈ R} (transitive)
[Intext Question]
Solved Examples
Q.1. If A is a set of all triangles and the relation R is defined by “is congruent to” prove that R is an equivalence relation.
Ans.
(i) R is reflexives as every triangle is congruent to itself.
(ii) R is symmetric: if a triangle x is congruent to another triangle y, then the triangle y is congruent to the triangle x.
(iii) If ‘a triangle x is congruent to a triangle y and y is congruent to a third triangle z, then x is also congruent to z.
Hence the relation R is transitive. (i), (ii) and (iii) ⇒ that the relation R is an equivalence relation.
Q.2. Three friends A, B, and C live near each other at a distance of 5 km from one another. We define a relation R between the distances of their houses. Is R an equivalence relation?
Ans.
- For an equivalence Relation, R must be reflexive, symmetric and transitive.
- R is not reflexive as A cannot be 5 km away to itself.
- The relation, R is symmetric as the distance between A & B is 5 km which is the same as the distance between B & A.
- R is transitive as the distance between A & B is 5 km, the distance between B & C is 5 km and the distance between A & C is also 5 km. Therefore, this relation is not equivalent.
Equivalence class
An equivalence class is subset of a given set in which each element is related with each other. Moreover equivalence class can be found if the given relation on given set is an equivalence relation.
Example: Let A = {1, 3, 5, 9, 11, 18} and a relation on A given by
R = {(a, b) | a - b is divisible by 4 } find all equivalence classes.
Solution. Clearly R ={(1, 1), (3, 3), (5, 5), (9, 9), (11, 11), (18, 18), (1, 5)(5, 1), (1, 9), (3, 11)(11, 3), (5, 9), (9, 5)}
Now A1 = {1, 5, 9}, A2 = {3, 11}, A3= {18}
Hence A1, A2, A3 are called equivalence classes of a set A on the given relation R
Moreover we can represent these classes in a very specific way as below:
A1 = [1] or [5] or [9]
A2 = [3] or [11]
A3 = [18]
Clearly, A1, A2 , A3 are disjoint and A1∪ A2 ∪ A3 = A and A1 ∩ A2 ∩ A3= ∅
Note:
- All elements of Ai are related to each other, for all i.
- No element of Ai is related to any element of Aj, i≠ j.
- ∪ Aj = X and Ai ∩Aj = ∅, i ≠ j.
The subsets Ai are called equivalence classes and are called partitions or subdivisions of set A and these are mutually disjoint to one another.
Short Answer Type Questions
Q.1. Show that the number of equivalence relation in the set {1, 2, 3} containing (1, 2) and (2, 1) is two.
Ans. A = {1, 2, 3}
The maximum possible relation (i.e. universal relation) is
R = {(1, 1), (2, 2), (3, 3), (1, 2), (1, 3), (2, 1), (2, 3), (3, 1), (3, 2)}
The smallest equivalence relation R1 containing (1 , 2) and (2 , 1) is
R1 = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 1)}
we are left with four pairs (from universal relation) i.e. (2, 3), (3, 2), (1, 3) and (3, 1)
If we add (2, 3) to R1, then for symmetric by we must add (3, 2) and now for transitivity we are forced to add (1, 3) and (3, 1)
Thus the only relation bigger than R1 is universal relation i.e R
∴ The no. of equivalence relations containing (1, 2) and (2, 1) is two.
Q.2. If 𝑅 = {(𝑥, 𝑦) ∶ 𝑥2 + 𝑦2 ≤ 4 ; 𝑥, 𝑦 ∈ 𝑧} is a relation on 𝑧. Write the domain of R.
Ans. R = {(0, 1), (0, -1), (0, 2), (0, -2), (1, 1), (1, -1), (-1, 0), (-1, 1), (-1, -1), (2, 0), (-2, 0)}
∴ Domain of R = {0, 1 , -1, 2, -2}
(i.e the first domain of each ordered pairs)
Q.3. Let R = {(𝑥, 𝑦) : ∣𝑥2 − 𝑦2∣ < 1} be a relation on set A = {1, 2, 3, 4, 5}. Write R as a set of ordered pairs.
Ans. A = {1, 2, 3, 4, 5}
for ∣𝑥2 − 𝑦2∣ < 1 : 𝑥 should be equal to 𝑦
∴ R = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5)}
Q.4. R is a relation in Z defined as (𝑎, 𝑏) ∈ 𝑅 ⇔ 𝑎2 + 𝑏2 = 25. Find the range.
Ans. We have, 𝑎2 + 𝑏2 = 25 and 𝑎 , 𝑏 ∈ 𝑧
∴ R = {(0, 5), (0, -5), (3, 4), (3, -4), (-3, 4), (-3, -4), (4, 3), (4, -3), (-4, 3), (-4, -3), (5, 0), (-5, 0)}
∴ Range = {-5, 5, 4, -4, 4, 3, -3, 0}
(i.e. second elements of each order pairs)
[Intext Question]
What is Function?
A relation from A to B is a function if every element of set A has one and only one image in set B. Therefore, for a function,
Every element of set A will have an image.
Every element of set A will have only have one image in set B.
Let us take an example now. Let A = {1, 2, 3, 4, 5} and B= {2, 4, 6, 8, 1}
As we have discussed above that for every element of set A will have an image. And we can see that elements 4 and 6 does not have any image. Also,every element of set A should have only one image in set B but as you can see that elements 2,3 and 4 have same image,6. Therefore, it is not a function.
Note: In a function, domain will always be equal to first set.
Example 1: Is the relation expressed in the mapping diagram a function?
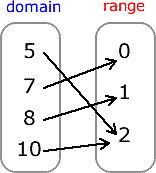
Each element of the domain is being traced to one and only element in the range. However, it is okay for two or more values in the domain to share a common value in the range. That is, even though the elements 5 and 10 in the domain share the same value of 2 in the range, this relation is still a function.
Example 2: Is the relation expressed in the mapping diagram a function?
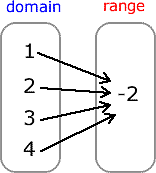
What do you think? Does each value in the domain point to a single value in the range? Absolutely! There’s nothing wrong when four elements coming from the domain are sharing a common value in the range. This is a great example of a function as well.
Example 3: Is the relation expressed in mapping diagram a function?
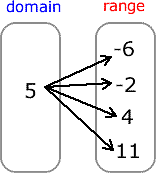
If you think example 3 was “bad”, this is “worse”. A single element in the domain is being paired with four elements in the range. Remember, if an element in the domain is being associated with more than one element in the range, the relation is automatically disqualified to be a function. Thus, this relation is absolutely not a function.
Example 4: Is the mapping diagram a relation, or function?
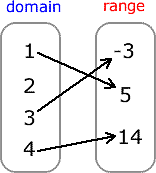
Let me throw in this example to highlight a very important idea. Your teacher may give something like this just to check if you pay attention to details.
So far it looks normal. But there’s a little problem. The element “2” in the domain is not being paired with any element in the range. Every element in the domain must have some kind of correspondence to the range for it be considered a relation at least. Since this is not a relation, it follows that it can’t be a function.
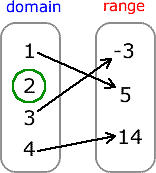
So, the final answer is neither a relation nor a function.
[Intext Question]
Composite Functions
Let f: X → Y1 and g: Y2 → Z be two functions and the set D = {x ∈ X: f(x) ∈ Y2}. If D ≡ Ø, then the function h defined on D by h(x) = g{f(x)} is called composite function of g and f and is denoted by gof. It is also called function of a function.

Remark: Domain of gof is D which is a subset of X (the domain of f). Range of gof is a subset of the range of g. If D = X, then f(X) ⊆ Y2.
Properties of composite functions
- The composite of functions is not commutative i.e. gof ≠ fog.
- The composite of functions is associative i.e. if f, g, h are three functions such that fo (goh) & (fog) oh are defined, then fo (goh) = (fog) oh.
Example 1. Let f(x) = ex ; R+ → R and g(x) = sin-1 x; [-1, 1] →[- π/2 , π/2]. Find domain and range of fog (x)
Solution. Domain of f(x): (0, ∞), Range of g(x): [- π/2 , π/2]
The values in range of g(x) which are accepted by f(x) are (0, π/2]
⇒ 0 < g(x) ≤ π/2 0 < sin-1 x ≤ π/2 , 0 < x ≤ 1
Hence domain of fog(x) is x ∈ (0, 1]

Example 2. Let f(x) = (x-1)/(x+1) , f2(x) = f{f(x)}, f3 (x) = f{f2(x)},.....fk + 1 (x) = f{fk(x)}. for k = 1, 2, 3,...., Find f1998 (x).
Solution.



Thus, we can see that fk(x) repeats itself at intervals of k = 4.
Hence, we have f1998(x) = f2(x) = -1/x, [∴ 1998 = 499 × 4 + 2]
Example 3. Let g : R → R be given by g(x) = 3 + 4x. If gn(x) = gogo....og(x), show that fn(x) = (4n - 1) + 4nx if g-n (x) denotes the inverse of gn (x).
Solution. Since g(x) = 3 + 4x
g2(x) = (gog) (x) = g {g (x)} = g (3 + 4x) = 3 + 4 (3 + 4x) or g2(x) = 15 + 42x = (42 – 1) + 42x
Now g3(x) = (gogog) x = g {g2 (x)} = g (15 + 42 x) = 3 + 4 (15 + 42 x) = 63 + 43 x = (43 –1) + 43x
Similarly we get gn(x) = (4n – 1) + 4nx
Now let gn (x) = y ⇒ x = g–n(y) ....(1)
∴ y = (4n – 1) + 4nx or x = (y + 1 – 4n)4–n ...(2)
From (1) and (2) we get g–n (y) = (y + 1 – 4n) 4–n.
Hence g–n (x) = (x + 1 – 4n) 4–n
Example 4. If f(x) = If f(x) = | |x – 3| – 2 | ; 0 ≤ x ≤ 4 and g(x) = 4 – |2 – x| ; –1 ≤ x ≤ 3 then find fog(x).
Solution.






Example 5. Prove that f(n) = 1 - n is the only integer valued function defined on integers such that
(i) f(f(n)) = n for all n ε Z and
(ii) f(f(n + 2) + 2) = n for all n ε Z and
(iii) f(0) = 1.
Solution. The function f(n) = 1 - n clearly satisfies conditions (i), (ii) and (iii). Conversely, suppose a function
f: Z → Z satisfies (i), (ii) and (iii). Applying f to (ii) we get, f(f(f(n + 2) + 2))) = f(n) and this gives because of (i), f(n + 2) + 2 = f(n), ........(1)
for all n ε Z. Now using (1) it is easy to prove by induction on n that for all n ε Z,
Also by (iii), f(0) = 1. Hence by (i), f(1) = 0. Hence f(n) = 1 - n for all n ε Z.
[Intext Question]
General Definition
- Identity function: A function f ; A → defined by f(x) = x ∀ x ∈ A is called the identity of A & denoted by IA.
Ex: f : R+ → R+ ; f(x) = eℓnx and f : R → R ; f(x) = ℓn ex
Every Identity function is a bijection. - Constant function: A function f: A → B is said to be constant function. If every element of set A has the same functional image in set B i.e. f: A → B ; f(x) = c ∀ x ε A & c ε B is called constant function.
- Homogeneous function: A function is said to be homogeneous w.r.t. any set of variables when each of its term is of the same degree w.r.t. those variables.
- Bounded Function: A function y = f(x) is said to be bounded if it can be express is the form of
a ≤ f(x) ≤ b where a and b are finite quantities.
Example: -1 ≤ sin x ≤ 1 ; 0 ≤ {x} < 1 ; -1 ≤ sgn (x) ≤ 1 but ex is not bounded.
Any function having singleton range like constant function. - Implicit function & Explicit function: If y has been expressed entirely in terms of `x' then it is called an explicit function.
If x & y are written together in the form of an equation then it is known as implicit equation corresponding to each implicit equation there can be one, two or more explicit function satisfying it
Example:
y = x3 + 4x2 + 5x → Explicit function
x + y = 1 → Implicit equation
y = 1 - x → Explicit function - Even & Odd Functions
Function must be defined in symmetric interval [-x, x]
If f (-x) = f (x) for all x in the domain of `f' then f is said to be an even function.
e.g. f (x) = cos x; g (x) = x² + 3.
If f (-x) = -f (x) for all x in the domain of `f' then f is said to be an odd function.
e.g. f (x) = sin x ; g (x) = x3 + x.
Remark
- f (x) - f (-x) = 0 ⇒ f (x) is even & f (x) + f (-x) = 0 ⇒ f (x) is odd.
- A function may be neither even nor odd.
- Inverse of an even function is not defined.
- Every even function is symmetric about the y-axis & every odd function is symmetric about the origin.
- A function (whose domain is symmetric about origin) can be expressed as a sum of an even & an odd function. e.g.

- The only function which is defined on the entire number line & is even and odd at the same time is f(x) = 0.
- If f and g both are even or both are odd then the function f.g will be even but if any one of them is odd and other even then f.g will be odd.
Example 6. Which of the following functions is odd ?
(a) sgn x + x2000
(b) | x | - tan x
(c) x3 cot x
(d) cosec x55
Solution.
Let’s name the function of the parts (A), (B), (C) and (D) as f(x), g(x), h(x) & f(x) respectively. Now
(a) f(–x) = sgn (–x) + (–x)2000 = –sgn x + x2000 ≠ f(x) & ≠ –f(x) ∴ f is neither even nor odd.
(b) g(–x) = |–x| – tan (–x) = |x| + tan x ∴ g is neither even nor odd.
(c) h(–x) = (–x)3 cot (–x) = –x3 (–cot x) = x3 cot x = h(x) ∴ h is an even function
(d) f(–x) = cosec (–x)55 = cosec (–x55) = –cosec x55 = – f(x) ∴ f is an odd function.
Alternatively
(a) f(x) = sgn (x) + x2000 = O + E = neither E nor O
(b) g(x) = E – O = Neither E nor O
(c) h(x) = O × O = E (D) f(–x) = O o O = O
(d) is the correct option
Example 7. 
(a) An even function
(b) An odd function
(c) Neither even nor odd function
(d) None of these
Solution.
= O × eO × O = O × eE = O × E = O
Example 8. Let f: [-2, 2] → R be a function if f(x) = 
so that
(i) f is an odd function
(ii) f is an even function (where [*] denotes the greatest integer function)
Solution.


(i) If f is an odd function then f(x) = –f (–x)
(ii) If f is an even function 
Example 9. Let f(x) = ex + sin x be defined on the interval [-4, 0]. Find the odd and even extension of f(x) in the interval [-4, 4].
Solution.
Odd Extension: Let g0 be the odd extension of f(x), then
Even Extension: Let ge be the odd extension of f(x), then
Classification of Functions:
1. One-One Function (Injective mapping): A function f: A → B is said to be a one-one function or injective mapping if different elements of A have different f images in B. Thus for x1, x2 ∈ A & f(x1), f(x2) ∈ B, f(x1) = f(x2) ⇔ x1 = x2 or x1 ≠ x2 ⇔ f(x1) ≠ f(x2).
Diagrammatically an injective mapping can be shown as

OR 
Remark:
(i) Any function which is entirely increasing or decreasing in its domain, is one-one.
(ii) If any line parallel to the x-axis cuts the graph of the function at most at one point, then the function is one-one.
Q.1. Determine if the function given below is one to one.
(i) To each state of India assign its Capital
Ans. This is not one to one function because each state of India has not different capital.
(ii) Function = {(2, 4), (3, 6), (-1, -7)}
Ans. The above function is one to one because each value of range has different value of domain.
(iii) f(x) = |x|
Ans. Here to check whether the given function is one to one or not, we will consider some values of x (domain) and from the given function find the value of range(y).

From the above table we can see that an element in the range repeats, then this is not a one to one function.
Q.2. Without using graph prove that the function
F : R → R defiend by f (x) = 4 + 3x is one-to-one
Ans. For a function to be one-one function if
F (x1) = F (x1) ⇒ x1 = x2 ∀ x1, x2 ∈ domain
∴ Now f (x1) = f (x2) gives
4 + 3x1 = 4 + 3x2 or x1 = x2
∴ F is a one-one function.
(2) Many-One function: A function f: A → B is said to be a many one function if two or more elements of A have the same f image in B. Thus f: A → B is many one if for
x1, x2 ∈ A, f(x1) = f(x2) but x1≠ x2
Diagrammatically a many one mapping can be shown as

OR

Remark:
(i) A continuous function f(x) which has at least one local maximum or local minimum, is many-one. In other words, if a line parallel to x-axis cuts the graph of the function at least at two points, then f is many-one.
(ii) If a function is one-one, it cannot be many-one and vice versa.
(iii) If f and g both are one-one, then fog and gof would also be one-one (if they exist).
Q.3. Without using graph check the following function f: R → R defined by f (x) = x2 is one-to-one or not ?
Ans. For the function to be one to one , different elements must have different images
But here if x = 1 then f(1) = (1)2 =1
And if x = -1 then f(-1) =(-1)2 = 1
Clearly, x = 1 and x = -1 both have same image
So given function is not one to one i.e many to one function
In other words, we can say that a function which is not one to one that can be known as many to one.
Example 16. Show that the function f(x) = (x2 - 8x + 18)/(x2 + 4x + 30) is not one-one.
Solution. Test for one-one function
A function is one-one if f(x1) = f(x2) ⇒ x1 = x2


Since f(x1) = f(x2) does not imply x1 = x2 alone, f(x) is not a one-one function.
Example 17. Let f be an injective function such that f(x) f(y) + 2 = f(x) + f(y) + f(xy) ∀ x, y ∈ R.
If f(4) = 65 and f(0) ≠ 2, then show that f(x) – 1= x3 for x ∈ R
Solution. Given that f(x) f(y) + 2 = f(x) + f(y) + f(xy) ....(i)
Putting x = y = 0 in equation (i), we get f(0) f(0) + 2 = f(0) + f(0) + f(0)
or (f(0))2 + 2 = 3f(0) or (f(0) – 2) (f(0) – 1) = 0 or f(0) = 1 (∴ f(0) ≠ 2) ....(ii)
Again putting x = y = 1 in equation (i) and repeating the above steps, we get (f(1) – 2) (f(1) – 1) = 0
But f(1) ≠ 1 as f(x) is injective.
∴ f(1) = 2 ...(iii)
Now putting y = 1/x in equation (i), we get






Let f(x) – 1 = g(x)

from equation (iv), we get g(x) g(1/x) = 1 which is only possible when
g(x) = ± xn
f(x) = ± xn + 1
or f(x) = ± xn + 1 or 65 = ± 4n + 1
or 4n = 64 = (4)3
n = 3
f(x) = x3 + 1 or f(x) – 1 = x3 (neglecting negative sign)
3. Onto-function (Surjective mapping): If the function f: A → B is such that each element in B (co-domain) is the f image of at least one element in A, then we say that f is a function of A 'onto' B. Thus f: A → B is surjective if ∀ b ∈ B, ∃ some a ∈ such that f (a) = b.
Diagramatically surjective mapping can be shown as

OR

Note that: if range ≡ co-domain, then f(x) is onto.
Q.4. If f: R → R is defined as f (x)= 3x + 7, x ∈ R, then show that f is an onto function.
Ans. We have f (x) = 3x + 7, x ∈ R . Let b ∈ R so that f (x) = b ⇒ 3x + 7 = b or
x = (b - 7)/3. Since b ∈ R, (b - 7)/3 ∈ R.
⇒ b is image of (b - 7)/3 where b is arbitrary.
Hence f (x) is an onto function.
4. Into function: If f: A → B is such that there exists at least one element in co-domain which is not the image of any element in the domain, then f(x) is into.
Diagramatically into function can be shown as

Remark:
(i) If a function is onto, it cannot be into and vice versa.
(ii) If f and g are both onto, then gof or fog would be onto (if exists).
Thus a function can be one of these four types:
(a) One-one onto (injective & surjective)

(b) One-one into (injective but not surjective)

(c) Many-one onto (surjective but not injective)

(d) many-one into (neither surjective nor injective)

Remark:
(i) If f is both injective & surjective, then it is called a Bijective function. Bijective functions are also named as invertible, non singular or biuniform functions.
(ii) If a set A contains n distinct elements then the number of different functions defined from A → A is nn & out of it n ! are one-one.
(iii) The composite of two bijections is a bijection i.e. if f & g are two bijections such that gof is defined, then gof is also a bijection.
Q. Prove that
F : R → R defined by f (x) = 4x3 - 5 is a bijection
Ans. Now f (x1) = f (2) ∀ x1, x2 Domain
∴ 4x1 3 - 5 = 4x23 - 5
⇒ x1 3 = x23
⇒ x1 3 - x23 = 0 ⇒ (x2 - x1) (x12 + x1x2 + x22) = 0
⇒ x1 = x2 or
x12 + x1x2 + x22 = 0 (rejected).
It has no real value of x1 and x2.
∴ F is a one-one function.
Again let y = (x) where y ∈ codomain, x ∈ domain.
We have y = 4x3 - 5
or 
∴ For each y ∈ codomain ∃ x ∈ domain such that f (x) = y.
Thus F is onto function.
∴ F is a bijection.
Example 18. A function is defined as , f: D → R f(x) = cot-1 (sgn x) + sin-1(x - {x}) (where {x} denotes the fractional part function) Find the largest domain and range of the function. State with reasons whether the function is injective or not. Also draw the graph of the function.
Solution. f is many one


Example 19. Find the linear function(s) which map the interval [0 , 2 ] onto [1 , 4 ].
Solution. Let f (x) = a x + b
f (0) = 1 & f (2) = 4 ⇒ b = 1 & a =3/2
or f (0) = 4 & f (2) = 1 ⇒ b = 4 & a = -3/2
f(x) = 3x/2 + 1 or f(x) = 4 - 3x/2
Example 20.
(i) Find whether f(x) = x + cos x is one-one.
(ii) Identify whether the function f(x) = -x3 + 3x2 - 2x + 4 ; R → R is ONTO or INTO
(iii) f(x) = x2 - 2x + 3; [0, 3] → A. Find whether f(x) is injective or not.
Also find the set A, if f(x) is surjective.
Solution.
(i) The domain of f(x) is R. f'(x) = 1 – sin x.
f'(x) ≥ 0 for all x ∈complete domain and equality holds at discrete points only
∴ f(x) is strictly increasing on R. Hence f(x) is one-one
(ii) As codomain ≡ range, therefore given function is ONTO
(iii) f'(x) = 2(x – 1); 0 ≤ x ≤ 3


f(x) is a non monotonic continuous function. Hence it is not injective.
For f(x) to be surjective, A should be equal to its range. From graph, range is [2, 6]
∴ A ≡ [2, 6]
Example 21. If f and g be two linear functions from [-1, 1] onto [0, 2] and  be defined by
be defined by

Solution. Let h be a linear function from [-1, 1] onto [0, 2].
Let h(x) = ax + b, then h'(x) = a
If a > 0, then h(x) is an increasing function & h(–1) = 0 and h(1) = 2 ⇒ –a + b = 0 and a + b = 2 ⇒ a = 1 & b = 1.
Hence h(x) = x + 1.
If a < 0, then h(x) is a decreasing function & h(–1) = 2 and h(1) = 0 ⇒ –a + b = 2 and a + b = 0 ⇒ a = –1 & b = 1.
Hence h(x) = 1 – x
Now according to the question f(x) = 1 + x & g(x) = 1 - x
or f(x) = 1 – x & g(x) = 1 + x


 ,
, 
In both cases, |Ø(Ø(x)) + Ø(Ø(1/x)) | 
ALGEBRA OF REAL FUNCTIONS
Real-valued Mathematical Functions
In mathematics, a real-valued function is a function whose values are real numbers. It is a function that maps a real number to each member of its domain. Also, we can say that a real-valued function is a function whose outputs are real numbers i.e., f: R → R (R stands for Real).

Algebra of Real Functions
In this section, we will get to know about addition, subtraction, multiplication, and division of real mathematical functions with another.
Addition of Two Real Functions
Let f and g be two real valued functions such that f: X → R and g: X → R where X ⊂ R. The addition of these two functions (f + g) : X → R is defined by:
(f + g) (x) = f(x) + g(x), for all x ∈ X
Subtraction of One Real Function from the Other
Let f : X → R and g : X → R be two real functions where X ⊂ R. The subtraction of these two functions (f – g): X → R is defined by:
(f – g) (x) = f(x) – g(x), for all x ∈ X
Multiplication by a Scalar
Let f: X → R be a real-valued function and γ be any scalar (real number). Then the product of a real function by a scalar γf: X → R is given by:
(γf) (x) = γ f(x), for all x ∈ X.
Equal functions
Let f and g be two functions defined from A to B. Then f , g : A → B are equal if f (x) = g(x), x ∈ A .
If the function f and g are equal, then the subsets, graph of f and graph of g, of A x B are equal.
Q.1. 
find the value of k
Ans. We need to consider only one equation
2k = 6
k = 3
Q.2. Find the values of x and y.
Ans:
2x – 6 = 5
2x = 11
x = 5.5
4 – y = 3
y = 1
Multiplication of Two Real Functions
The product of two real functions say, f and g such that f: X → R and g: X → R, is given by
(fg) (x) = f(x) g(x), for all x ∈ X
Division of Two Real Functions
Let f and g be two real-valued functions such that f: X → R and g: X → R where X ⊂ R. The quotient of these two functions (f ⁄ g): X → R is defined by:
(f / g) (x) = f(x) / g(x), for all x ∈ X, but g(x) ≠ 0 for all x ∈ X
Note: It is also called point wise multiplication.
Solved Example
Q. Let f(x) = x3 and g(x) = 3x + 1 and a scalar, γ= 6. Find
(a) (f + g) (x)
(b) (f – g) (x)
(c) (γf) (x)
(d) (γg) (x)
(e) (fg) (x)
(f) (f / g) (x)
Sol: We have,
(a) (f + g) (x) = f(x) + g(x) = x3 + 3x + 1.
(b) (f – g) (x) = f(x) – g(x) = x3 – (3x + 1) = x3 – 3x – 1.
(c) (γf) (x) = γ f(x) = 6x3
(d) (γg) (x) = γ g(x) = 6 (3x + 1) = 18x + 6.
(e) (fg) (x) = f(x) g(x) = x3 (3x +1) = 3x4 + x3.
(f) (f / g) (x) = f(x) / g(x) = x3 / (3x + 1), provided x ≠ – 1/3.
BINARY OPERATIONS
We get a number when two numbers are either added or subtracted or multiplied or are divided. The binary operations associate any two elements of a set. The resultant of the two are in the same set. Binary operations on a set are calculations that combine two elements of the set (called operands) to produce another element of the same set.
The binary operations * on a non-empty set A are functions from A × A to A. The binary operation, *: A × A → A. It is an operation of two elements of the set whose domains and co-domain are in the same set.

Addition, subtraction, multiplication, division, exponential is some of the binary operations.
Properties of Binary Operation
- Closure property: An operation * on a non-empty set A has closure property, if a ∈ A, b ∈ A ⇒ a * b ∈ A.
- Additions are the binary operations on each of the sets of Natural numbers (N), Integer (Z), Rational numbers (Q), Real Numbers(R), Complex number(C).
The additions on the set of all irrational numbers are not the binary operations.
- Multiplication is a binary operation on each of the sets of Natural numbers (N), Integer (Z), Rational numbers (Q), Real Numbers(R), Complex number(C).
Multiplication on the set of all irrational numbers is not a binary operation.
- Subtraction is a binary operation on each of the sets of Integer (Z), Rational numbers (Q), Real Numbers(R), Complex number(C).
Subtraction is not a binary operation on the set of Natural numbers (N).
- A division is not a binary operation on the set of Natural numbers (N), integer (Z), Rational numbers (Q), Real Numbers(R), Complex number(C).
- Exponential operation (x, y) → xy is a binary operation on the set of Natural numbers (N) and not on the set of Integers (Z).
Properties of Binary Operations
Commutative
A binary operation * on a set A is commutative if a * b = b * a, for all (a, b) ∈ A (non-empty set). Let addition be the operating binary operation for a = 8 and b = 9, a + b = 17 = b + a.
Associative
The associative property of binary operations hold if, for a non-empty set A, we can write (a * b) *c = a*(b * c). Suppose N be the set of natural numbers and multiplication be the binary operation. Let a = 4, b = 5 c = 6. We can write (a × b) × c = 120 = a × (b × c).
Distributive
Let * and o be two binary operations defined on a non-empty set A. The binary operations are distributive if a*(b o c) = (a * b) o (a * c) or (b o c)*a = (b * a) o (c * a). Consider * to be multiplication and o be subtraction. And a = 2, b = 5, c = 4. Then, a*(b o c) = a × (b − c) = 2 × (5 − 4) = 2. And (a * b) o (a * c) = (a × b) − (a × c) = (2 × 5) − (2 × 4) = 10 − 6 = 2.
Identity
If A be the non-empty set and * be the binary operation on A. An element e is the identity element of a ∈ A, if a * e = a = e * a. If the binary operation is addition(+), e = 0 and for * is multiplication(×), e = 1.
Inverse
If a binary operation * on a set A which satisfies a * b = b * a = e, for all a, b ∈ A. a-1 is invertible if for a * b = b * a= e, a-1 = b. 1 is invertible when * is multiplication.
Note: 1. Identity element is unique for whole given set A(if exists) i.e each element of given set A has same identity element.
2. But inverse element is different for different elements(if exists) , but unique.
Solved Example
Q.1. Show that division is not a binary operation in N nor subtraction in N.
Solution. Let a, b ∈ N
Case 1: Binary operation * = division(÷)
–: N × N→N given by (a, b) → (a/b) ∉ N (as 5/3 ∉ N)
Case 2: Binary operation * = Subtraction(−)
–: N × N→N given by (a, b)→ a − b ∉ N (as 3 − 2 = 1 ∈ N but 2−3 = −1 ∉ N).
Q.2. Let A = {−1, 1, 2, 3}. Construct the binary table corresponding to the binary operation “multiplication” on A.
Solution. We have the following binary (or composition) table:
|
209 videos|443 docs|143 tests
|
FAQs on Notes: Relations and Functions - Mathematics (Maths) for JEE Main & Advanced
| 1. What is the difference between a relation and a function? |  |
| 2. How can a relation be represented graphically? |  |
| 3. What is the domain and range of a relation? |  |
| 4. How many total relations can be formed between two sets with m and n elements, respectively? |  |
| 5. What are the different types of relations? |  |
|
209 videos|443 docs|143 tests
|

|
Explore Courses for JEE exam
|

|


















