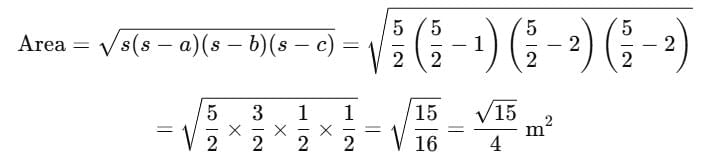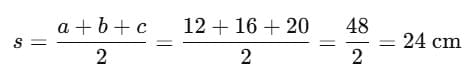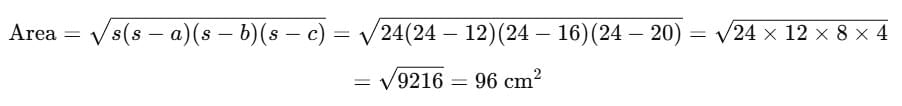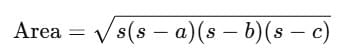Solved Question and Answers: Heron's Formula | Mathematics (Maths) Class 9 PDF Download
Q1: The sides of the triangle are 56 cm, 60 cm and 52 cm long. Then the area of the triangle is:
(A) 1322 cm2
(B) 1311 cm2
(C) 1344 cm2
(D) 1392 cm2
Ans: (b) 1344 cm2
Sol: As per the question,
Sides of the triangle,
a = 56, b = 60, c = 52
s = (a + b + c)/2
⇒ s = (56 + 60 + 52)/2
= 168/2
= 84
Area of the triangle = √s (s-a) (s-b) (s-c)
= √84 (84-56) (84-60) (84-52)
= √84 × 28 × 24 × 32
= 1344cm2
Q2: Find the area of a triangle, two sides of which are 8 cm and 11 cm and the perimeter is 32 cm.
(A) 8 √30 cm²
(B) 5 √30 cm²
(C) 7 √30 cm²
(D) 9 √30 cm²
Ans: (A), 8 √30 cm²
Sol:
Here we have perimeter of the triangle = 32 cm, a = 8 cm and b = 11 cm.
Third side c = 32 cm – (8 + 11) cm = 13 cm
So, 2s = 32, i.e., s = 16 cm,
s – a = (16 – 8) cm = 8 cm,
s – b = (16 – 11) cm = 5 cm,
s – c = (16 – 13) cm = 3 cm.
Therefore, area of the triangle = √[s (s – a) (s – b) (s – c)]
= √[16 × 8 × 5 × 3] cm²
= 8 √30 cm²
Q3: The sides of a triangular plot are in the ratio of 3 : 5 : 7 and its perimeter is 300 m. Find its area.
(A) 1500 m²
(B) 1550√3 m²
(C) 1500√3 m²
(D) 1300 m²
Ans: (B), 1550√3 m²
Sol:
Suppose that the sides, in metres, are 3x, 5x and 7x . Then we know that
3x + 5x + 7x = 300 (perimeter of the triangle)
Therefore, 15x = 300, which gives x = 20.
So the sides of the triangle are
3 × 20 m, 5 × 20 m and 7 × 20 m
i.e., 60 m, 100 m and 140 m.We have
s = (60 + 100 + 140) ÷ 2 m = 150 m,and area = √[150 (150 – 60) (150 – 100) (150 – 140)] m²
= √[150 × 90 × 50 × 10] m²
= 1500 √3 m²
Q4: The area of the triangle having sides 1 m, 2 m, and 2 m is :
(A)
(B)
(C)
(D)
Ans: (a)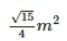
Sol: Given sides:
a = 1 m, b = 2 m, c = 2 m
This is an isosceles triangle.First, calculate the semi-perimeter (s):
Now apply Heron’s formula:
Q5: The area of a triangle whose sides are 12 cm, 16 cm, and 20 cm is
(A) 96 cm2
(B) 320 cm2
(C) 240 cm2
(D) 72 cm2
Ans: (a) 96 cm2
Sol: Given sides:
a = 12 cm, b = 16 cm, c = 20 cmFirst, find the semi-perimeter (s):
Now, use Heron’s formula:
Q6: The difference between the semi-perimeter and the sides of △ABC is 8, 7, and 5 cm, respectively. Its semi-perimeter ‘s’ is
(A) 20 cm
(B) 5 cm
(C) 15 cm
(D) 10 cm
Ans: (a) 20 cm
Sol: Let the semi-perimeter of the triangle be s.
Let the sides of the triangle be a, b and c.
Given: s – a = 8, s – b = 7 and s – c = 5
Adding all the above equations, we get
(s – a) + (s – b) + (s – c) = 8 + 7 + 5
⇒ 3s – (a + b + c) = 20
⇒ 3s – 2s = 20 (∵ s = (a + b + c) / 2)
⇒ s = 20 cm
Thus the semi-perimeter is 20 cm.
Q7: The sides of a triangular flower bed are 5 m, 8 m, and 11 m. The area of the flower bed is
(A) √300 m2
(B) √330 m2
(C) 21√4 m2
(D) 4√21 m2
Ans: (d) 4√21 m2
Sol: First, we find the semi-perimeter, s, which is half the sum of the sides: s = (5 m + 8 m + 11 m) / 2 = 12 m.
Next, we calculate the differences between the semi-perimeter and each side:s - a = 12 m - 5 m = 7 m,
s - b = 12 m - 8 m = 4 m,
s - c = 12 m - 11 m = 1 m.
Area = √(s(s - a)(s - b)(s - c)) = √(12 m × 7 m × 4 m × 1 m) = √(336 m2).
= 4√21 m2
Q8: The product of the difference of the semi-perimeter and respective sides of △ABC is given as 13200 m3. The area of △ABC, if its semi-perimeter is 132m, is given by
(A) 132 m2
(B) 13200 m2
(C) 1320 m2
(D) 20√33 m2
Ans: (C) 1320 m2
Sol: We are given:
Semi-perimeter s=132 m
The product (s−a) (s−b) (s−c) = 13200 m3
We use Heron’s Formula for the area of a triangle:
Substitute the given values:
⇒
Thus, the area of △ABC is 1320 m2
Q9: A rhombus-shaped field has green grass for 18 cows to graze. If each side of the rhombus is 30 m and its longer diagonal is 48 m, how much area of grass field will each cow be getting?
(A) 42 m²
(B) 30 m²
(C) 32 m²
(D) 48 m²
Ans: (D) , 48 m²
Sol:
Consider the triangle BCD, Its semi-perimeter = (48 + 30 + 30)/2 m = 54 m
Using Heron’s formula,
Area of the ΔBCD= √[s(s – a)(s – b)(s – c)]
= (√[54 (54 – 48) (54 – 30) (54 – 30)]) m²
= (√[54 × 6 × 24 × 24]) m²
= 432 m².
Area of field = 2 × area of ΔBCD
= (2 × 432) m²
= 864 m².
Thus, the area of the grass field that each cow will be getting = (864 ÷ 18) m² = 48 m²
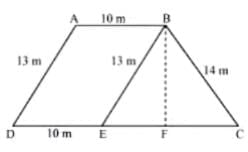
Q10. A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m. The non-parallel sides are 14 m and 13 m. Find the area of the field.
(A) 186 m².
(B) 198 m².
(C) 196 m².
(D) 188 m².
Ans: (C) , 196 m²
Sol:
It can be seen that the quadrilateral ABED is a parallelogram. So, AB = ED = 10 m and AD = BE = 13 m.
EC = 25 – ED = 25 – 10 = 15 m.Now, consider the triangle BEC. Its semi-perimeter (s) = (13 + 14 + 15) ÷ 2 = 21 m.
By using Heron’s formula,
Area of triangle BEC = √[s (s – a) (s – b) (s – c)]
= √[21 × (21 – 13) × (21 – 14) × (21 – 15)] m²
= √[21 × 8 × 7 × 6] m²
= 84 m².We also know that the area of triangle BEC = (½) × CE × BF = 84 cm² = (½) × 15 × BF
⇒ BF = (168 ÷ 15) cm = 11.2 cm.So, the total area of ABED will be BF × DE, i.e. 11.2 × 10 = 112 m².
Therefore, Area of the field = 84 + 112 = 196 m².
|
40 videos|564 docs|56 tests
|
FAQs on Solved Question and Answers: Heron's Formula - Mathematics (Maths) Class 9
| 1. What is Heron's Formula and how is it used to calculate the area of a triangle? |  |
| 2. Can Heron's Formula be applied to all types of triangles? |  |
| 3. How do you find the semi-perimeter using Heron's Formula? |  |
| 4. What is the significance of Heron's Formula in geometry? |  |
| 5. Can Heron's Formula be used with decimal numbers for side lengths? |  |