Translating and reflecting in four quadrants | Year 6 Mathematics PDF Download
What are transformations?
Translations and reflections are examples of transformations.
A transformation is a method of changing the position (and sometimes the size) of a shape.
Consider the grid below as an example we can use to describe this movement:
- The grid has a pair of axes, dividing it into four quadrants.
- The horizontal, or x-axis, is numbered from -5 to 5.
- The vertical, or y-axis, is also numbered from -5 to 5.
- The two axes intersect at right angles at the point known as the origin.
What is translation?
- When we translate a shape, every point on the shape moves the same distance and in the same direction.
- Translating a shape does not change its size or rotate it. The shape remains "the same way round," meaning the orientation stays the same.
- A simple example of a translation would be:
- Move the shape 4 units to the right and 5 units down.
What is reflection?
- We might be asked to reflect a shape in a given mirror line. This line of reflection could be the x-axis, y-axis, or any other line.
- When a shape is reflected, an image of that shape is created, similar to ‘flipping’ the shape over the line of reflection.
- We must ensure that each point on the original shape is the same distance from the line of reflection as the corresponding point on the reflected image.
- Translations and reflections are examples of transformations where both the original shape and the resulting image are congruent, meaning they have the same shape and size.
 |
Download the notes
Translating and reflecting in four quadrants
|
Download as PDF |
Examples
Example 1: Now look at this grid.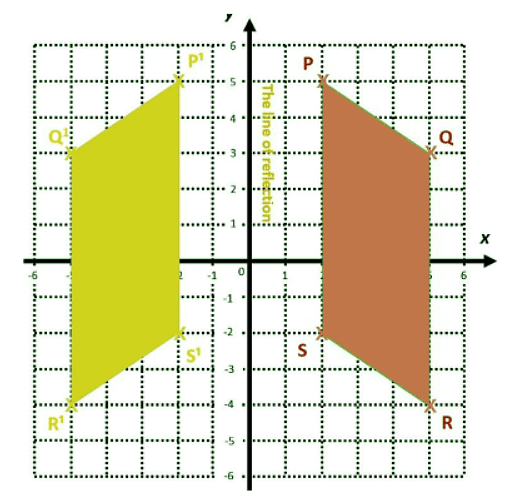
The parallelogram PQRS is positioned in the first and fourth quadrants.
The co-ordinates of the parallelogram are P(2,5), Q(5,3), R(5,-4) and S(2,-2).
The triangle PQRS has been reflected in the y axis (line of reflection).
The resulting image of this reflection has been labelled P¹Q¹R¹S¹.
Each point on the original shape is the same distance from the line of reflection as the corresponding point on the image.
The corresponding points are opposite one another following this ‘flip’. The two parallelograms are the same size and shape.
The two parallelograms are the same size and shape.
However, this transformation has changed the orientation of the original shape.
The parallelogram PQRS and the parallelogram P¹Q¹R¹S¹ are congruent.
Example 2: Look at this grid.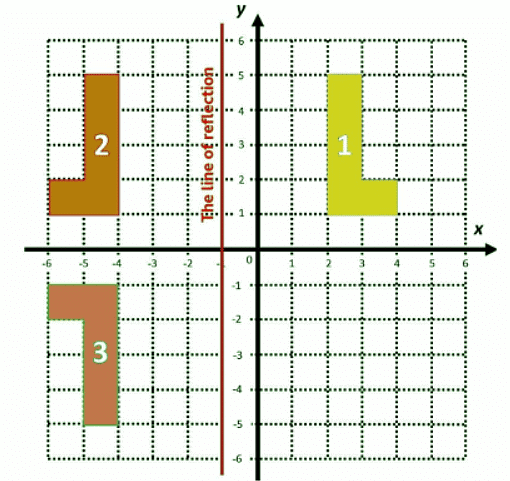 The L shape (irregular hexagon) labelled 1 is positioned in the first quadrant.
The L shape (irregular hexagon) labelled 1 is positioned in the first quadrant.
This shape is then reflected in a line that is parallel to the y axis.
This line of reflection is called the line x = -1
This is because the x coordinate of every point on the line will always be -1.
The resulting image has been labelled 2.
Now another reflection!
The L shape labelled 2 is now reflected in the x axis.
The resulting image has been labelled 3.
All three L shapes are the same shape and size and therefore they are all congruent.
|
54 videos|54 docs|17 tests
|
FAQs on Translating and reflecting in four quadrants - Year 6 Mathematics
| 1. What are transformations? |  |
| 2. What is translation? |  |
| 3. What is reflection? |  |
| 4. How are translating and reflecting used in four quadrants? |  |
| 5. Why do UK schools provide 5 meaningful FAQs about transformations? |  |















