Year 8 Exam > Year 8 Notes > Year 8 Mathematics IGCSE (Cambridge) > Angles and Constructions
Angles and Constructions | Year 8 Mathematics IGCSE (Cambridge) PDF Download
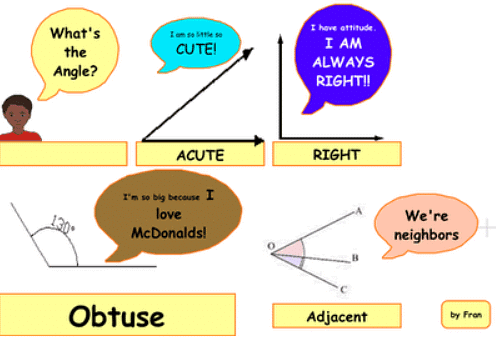
Types of Angles
Angles are formed when two lines or rays meet at a common point called the vertex.
Here are the main types of angles:
- Acute Angles: An acute angle is an angle that is less than 90 degrees.
- Example: A 45-degree angle is an acute angle.
- Right Angles: A right angle is exactly 90 degrees. It looks like the corner of a square or rectangle.
- Example: The angles in a piece of paper are right angles.
- Obtuse Angles: An obtuse angle is more than 90 degrees but less than 180 degrees.
- Example: A 120-degree angle is an obtuse angle.
- Straight Angles: A straight angle is exactly 180 degrees, forming a straight line.
- Example: The angle formed by a straight line is a straight angle.
- Reflex Angles: A reflex angle is more than 180 degrees but less than 360 degrees.
- Example: A 270-degree angle is a reflex angle.
- Full Rotation: A full rotation is 360 degrees.
- Example: A complete circle represents a full rotation.
Angle Properties
Understanding the properties of angles helps in solving various geometric problems.
Here are some important properties:
- Complementary Angles: Two angles are complementary if their sum is 90 degrees.
- Example: If one angle is 30 degrees, the complementary angle is 60 degrees (30° + 60° = 90°).
- Supplementary Angles: Two angles are supplementary if their sum is 180 degrees.
- Example: If one angle is 110 degrees, the supplementary angle is 70 degrees (110° + 70° = 180°).
- Adjacent Angles: Adjacent angles share a common side and vertex but do not overlap.
- Example: In a 'T' shape, the two angles on either side of the vertical line are adjacent.
- Vertically Opposite Angles: When two lines intersect, they form two pairs of vertically opposite angles. These angles are equal.
- Example: If two intersecting lines form angles of 50 degrees and 130 degrees, the vertically opposite angles are also 50 degrees and 130 degrees.
- Angles on a Straight Line: The sum of angles on a straight line is 180 degrees.
- Example: If one angle on a straight line is 70 degrees, the other angle is 110 degrees (70° + 110° = 180°).
- Angles Around a Point: The sum of angles around a point is 360 degrees.
- Example: If three angles around a point are 90 degrees, 120 degrees, and 60 degrees, the fourth angle is 90 degrees (90° + 120° + 60° + 90° = 360°).
Question for Angles and Constructions
Try yourself:
Which type of angle is formed when the sum of two angles is 180 degrees?View Solution
Constructing Geometric Figures
Constructing geometric figures involves using tools like a ruler, compass, and protractor.
Here are some basic constructions:
Constructing a Perpendicular Bisector
- Draw a line segment AB.
- Place the compass point on A and draw an arc above and below the line.
- Without changing the compass width, place the compass point on B and draw another set of arcs intersecting the first set.
- Draw a line through the intersection points. This line is the perpendicular bisector of AB.
 |
Test: Angles and Constructions
|
Start Test |
Start Test
Constructing an Angle Bisector
- Draw an angle ∠ABC.
- Place the compass point on B and draw an arc that intersects both sides of the angle.
- Place the compass point on one intersection and draw an arc inside the angle.
- Without changing the compass width, place the compass point on the other intersection and draw another arc intersecting the first arc.
- Draw a line from B through the intersection of the arcs. This line bisects ∠ABC.
Constructing a Triangle Given Three Sides (SSS)
- Draw the base of the triangle using a ruler.
- Place the compass point on one end of the base and draw an arc with a radius equal to one of the other sides.
- Without changing the compass width, place the compass point on the other end of the base and draw another arc intersecting the first arc.
- Draw lines connecting the intersection point of the arcs to the ends of the base.
Constructing a Triangle Given Two Angles and a Side (ASA)
- Draw the given side of the triangle using a ruler.
- Use a protractor to draw one of the given angles at one end of the base.
- Use the protractor to draw the second angle at the other end of the base.
- Extend the sides of the angles until they intersect. This forms the triangle.
 |
Download the notes
Angles and Constructions
|
Download as PDF |
Download as PDF
Examples
Example 1: Constructing a Perpendicular Bisector
- Draw a line segment AB of 8 cm.
- Follow the steps for constructing a perpendicular bisector.
- The perpendicular bisector will divide AB into two equal parts of 4 cm each.
Example 2: Constructing an Angle Bisector
- Draw an angle ∠PQR of 60 degrees.
- Follow the steps for constructing an angle bisector.
- The angle bisector will divide ∠PQR into two equal angles of 30 degrees each.
Example 3: Constructing a Triangle Given Three Sides
- Given sides of 5 cm, 6 cm, and 7 cm.
- Follow the steps for constructing a triangle with these sides.
- Verify that the triangle has the correct side lengths.
The document Angles and Constructions | Year 8 Mathematics IGCSE (Cambridge) is a part of the Year 8 Course Year 8 Mathematics IGCSE (Cambridge).
All you need of Year 8 at this link: Year 8
|
42 videos|12 docs|24 tests
|
FAQs on Angles and Constructions - Year 8 Mathematics IGCSE (Cambridge)
| 1. What are the different types of angles? |  |
| 2. What are some properties of angles? |  |
Ans. Some properties of angles include the fact that the sum of the interior angles in a triangle is always 180 degrees, vertical angles are always congruent, and corresponding angles are equal when two parallel lines are intersected by a transversal.
| 3. How can geometric figures be constructed using angles and constructions? |  |
Ans. Geometric figures can be constructed using tools such as a compass and straightedge to create angles, lines, and shapes. By following specific instructions and measurements, various geometric figures can be accurately constructed.
| 4. What is the importance of understanding angles in mathematics? |  |
Ans. Understanding angles is important in mathematics as they are fundamental to geometry and trigonometry. Angles play a crucial role in the study of shapes, measurements, and spatial relationships, making them essential for solving various mathematical problems.
| 5. How can students practice and master their knowledge of angles and constructions? |  |
Ans. Students can practice and master their knowledge of angles and constructions by solving a variety of problems, working on geometric constructions, and exploring real-world applications of angles. Regular practice, hands-on activities, and seeking help from teachers or tutors can also aid in improving understanding and proficiency in this area of mathematics.
Related Searches




















