Angles | Year 9 Mathematics IGCSE (Cambridge) - Class 9 PDF Download
| Table of contents |

|
| Angles |

|
| Parallel Lines and Angles |

|
| Polygons and Angles |

|
| Representing Data |

|
Angles
Types of Angles
- Acute Angle: An angle less than 90 degrees.
- Right Angle: An angle exactly 90 degrees.
- Obtuse Angle: An angle between 90 and 180 degrees.
- Straight Angle: An angle exactly 180 degrees.
- Reflex Angle: An angle more than 180 degrees but less than 360 degrees.
Angle Relationships
- Adjacent Angles: Angles that share a common side and a common vertex.
- Complementary Angles: Two angles that add up to 90 degrees.
- Supplementary Angles: Two angles that add up to 180 degrees.
- Vertically Opposite Angles: Angles opposite each other when two lines intersect. They are always equal.
Examples
- If one angle is 30 degrees, the complementary angle is 60 degrees (90 - 30).
- If one angle is 120 degrees, the supplementary angle is 60 degrees (180 - 120).
Parallel Lines and Angles
Corresponding Angles
- When two parallel lines are cut by a transversal, corresponding angles are equal.
Alternate Interior Angles
- Alternate interior angles are equal when two parallel lines are cut by a transversal.
Co-Interior Angles
- Co-interior angles are on the same side of the transversal and add up to 180 degrees.
Examples
- If two parallel lines are cut by a transversal, and one corresponding angle is 70 degrees, the other corresponding angle is also 70 degrees.
- If one alternate interior angle is 85 degrees, the other alternate interior angle is also 85 degrees.
- If one co-interior angle is 110 degrees, the other co-interior angle is 70 degrees (180 - 110).
Polygons and Angles
Interior Angles of Polygons
- The sum of the interior angles of a polygon with n sides is (n − 2) × 180 degrees.
Exterior Angles of Polygons
- The sum of the exterior angles of any polygon is always 360 degrees.
Regular Polygons
In a regular polygon (where all sides and angles are equal):
- Each interior angle is
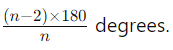
- Each exterior angle is
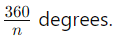
Examples
- For a triangle (3 sides):
- Sum of interior angles: (3 − 2) × 180 = 180 degrees.
- Each interior angle in an equilateral triangle: 180/3 = 60 degrees.
- For a square (4 sides):
- Sum of interior angles: (4 − 2) × 180 = 360 degrees.
- Each interior angle in a regular square: 360/4 = 90 degrees.
- For a pentagon (5 sides):
- Sum of interior angles: (5 − 2) × 180 = 540 degrees.
- Each interior angle in a regular pentagon: 540/5 = 108 degrees.
Representing Data
Types of Data
- Categorical Data: Data that can be divided into specific categories (e.g., colors, types of animals).
- Numerical Data: Data that consists of numbers and can be discrete (countable) or continuous (measurable).
Examples
- Categorical Data: Types of fruits (apples, oranges, bananas).
- Numerical Data: Heights of students in a class.
Data Representation
- Bar Charts: Used to represent categorical data with rectangular bars.
- Histograms: Used to represent numerical data with bars that touch each other, indicating the frequency of data within certain intervals.
- Pie Charts: Circular charts divided into sectors to represent parts of a whole.
- Line Graphs: Used to represent data points over time or another continuous variable.
Examples
- Bar Chart: Showing the number of students in different classes.
- Histogram: Representing the distribution of test scores in a class.
- Pie Chart: Displaying the market share of different companies.
- Line Graph: Tracking the temperature changes over a week.
The document Angles | Year 9 Mathematics IGCSE (Cambridge) - Class 9 is a part of the Class 9 Course Year 9 Mathematics IGCSE (Cambridge).
All you need of Class 9 at this link: Class 9
|
41 videos|55 docs|19 tests
|
FAQs on Angles - Year 9 Mathematics IGCSE (Cambridge) - Class 9
| 1. What are some common angles found in polygons? |  |
Ans. Some common angles found in polygons include interior angles, exterior angles, and central angles.
| 2. How can parallel lines create angles in a polygon? |  |
Ans. When parallel lines intersect a polygon, they create corresponding angles, alternate interior angles, and alternate exterior angles.
| 3. How do schools in the UK teach students about angles in polygons? |  |
Ans. Schools in the UK often use visual aids, interactive activities, and real-life examples to teach students about angles in polygons.
| 4. What types of data can be represented using angles in UK schools? |  |
Ans. Data such as survey results, weather patterns, and population demographics can be represented using angles in UK schools.
| 5. How do UK schools help students understand the importance of angles in real-world applications? |  |
Ans. UK schools often incorporate real-world scenarios, such as architecture, engineering, and navigation, to help students understand the practical significance of angles.
Related Searches



















