Probability | Year 9 Mathematics (Cambridge) PDF Download
| Table of contents |

|
| Basic Probability Concepts |

|
| Probability Calculations |

|
| Experimental and Theoretical Probability |

|
| Comparison |

|
Basic Probability Concepts
Probability is the measure of the likelihood that an event will occur. It is a number between 0 and 1, where 0 indicates an impossible event, and 1 indicates a certain event.
- Event: An outcome or a set of outcomes of an experiment.
- Experiment: A situation involving chance or probability that leads to results.
- Sample Space (S): The set of all possible outcomes.
Examples
- Flipping a Coin: The sample space is {Heads, Tails}. The probability of getting heads (P(H)) is 1/2.
- Rolling a Die: The sample space is {1, 2, 3, 4, 5, 6}. The probability of rolling a 4 (P(4)) is 1/6.
Probability Calculations
The probability of an event (A) is calculated as: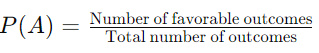
Examples
Example 1: Drawing a Red Card from a Deck
Sol: There are 52 cards in total and 26 red cards.
P(Red Card) = 26/52 = 1/2.
Example 2: Rolling an Even Number on a Die
Sol: There are 3 favorable outcomes (2, 4, 6) out of 6 total outcomes.
P(Even Number) = 3/6 = 1/2.
Experimental and Theoretical Probability
Theoretical Probability
Theoretical probability is determined by reasoning or calculation. It assumes that all outcomes in the sample space are equally likely.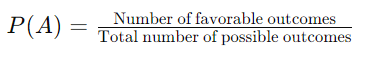
 |
Download the notes
Probability
|
Download as PDF |
Experimental Probability
Experimental probability is determined through actual experiments and observations. It is the ratio of the number of times an event occurs to the total number of trials.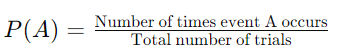
Examples
Example 1: Flipping a Coin 100 Times
Sol: If heads come up 55 times, the experimental probability of heads (P(H)) is:
P(H) = 55/100 = 0.55.
Example 2: Rolling a Die 60 Times
Sol: If a 3 is rolled 10 times, the experimental probability of rolling a 3 (P(3)) is:
P(3) = 10/60 = 1/6.
Comparison
- Theoretical probability is often used in ideal conditions, while experimental probability is used to verify theoretical predictions.
- Experimental probability can vary based on the number of trials, while theoretical probability remains constant.
Practice Problems
- Calculate the Probability of Drawing an Ace from a Deck of Cards:
- There are 4 aces in a deck of 52 cards.
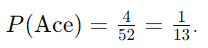
- Finding the Probability of Rolling a Number Greater than 4 on a Die:
- The favorable outcomes are {5, 6}.
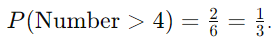
- Experimental Probability Example:
- If a coin is flipped 200 times and lands on tails 120 times, what is the experimental probability of tails?
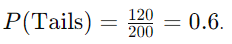
|
37 videos|12 docs|18 tests
|
FAQs on Probability - Year 9 Mathematics (Cambridge)
| 1. What is the basic concept of probability? |  |
| 2. How is probability calculated in statistics? |  |
| 3. What is the difference between theoretical probability and experimental probability? |  |
| 4. How can probability be used in decision-making? |  |
| 5. Can probability be used in everyday life? |  |



















