LU Decomposition | Engineering Mathematics for Computer Science Engineering - Computer Science Engineering (CSE) PDF Download
| Table of contents |

|
| Introduction |

|
| What is LU Decomposition? |

|
| LU Decomposition Method |

|
| Example of LU Decomposition |

|
Introduction
LU decomposition, named after the mathematicians Tadeusz Banachiewicz and Andrzej Walther, is a matrix decomposition method used in numerical analysis and linear algebra. It decomposes a matrix into the product of a lower triangular matrix (L) and an upper triangular matrix (U). This decomposition is particularly useful for solving systems of linear equations, matrix inversion, and determining matrix determinants efficiently.

What is LU Decomposition?
LU Decomposition expresses a given square matrix A as the product of two matrices:
- L: A lower triangular matrix with ones on the diagonal.
- U: An upper triangular matrix.
Mathematically, A can be written asA = LU
LU Decomposition Method
To factor any square matrix into two triangular matrices i.e., one is a lower triangular matrix and the other is an upper triangular matrix, we can use the following steps.
Given a set of linear equations, first convert them into matrix form A X = C where A is the coefficient matrix, X is the variable matrix and C is the matrix of numbers on the right-hand side of the equations.
Now, reduce the coefficient matrix A, i.e., the matrix obtained from the coefficients of variables in all the given equations such that for ‘n’ variables we have an nXn matrix, to row echelon form using Gauss Elimination Method. The matrix so obtained is U.
To find L, we have two methods. The first one is to assume the remaining elements as some artificial variables, make equations using A = L U, and solve them to find those artificial variables. The other method is that the remaining elements are the multiplier coefficients because of which the respective positions became zero in the U matrix. (This method is a little tricky to understand by words but would get clear in the example below)
Now, we have A (the nXn coefficient matrix), L (the nXn lower triangular matrix), U (the nXn upper triangular matrix), X (the nX1 matrix of variables), and C (the nX1 matrix of numbers on the right-hand side of the equations).
The given system of equations is A X = C. We substitute A = L U. Thus, we have L U X = C. We put Z = U X, where Z is a matrix or artificial variables and solve for L Z = C first and then solve for U X = Z to find X or the values of the variables, which was required.
Example of LU Decomposition
Solve the following system of equations using the LU Decomposition method
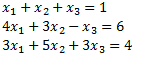
Sol: Here, we have A =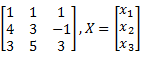
and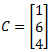
such that AX = C. Now, we first consider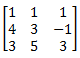
and convert it to row echelon form using Gauss Elimination Method. So, by doing
we get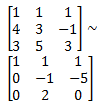
Now, by doing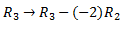
We get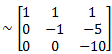
(Remember to always keep ' - ' sign in between, replace ' + 'sign by two ' - ' signs) Hence, we get L=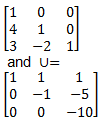
(notice that in L matrix,
l21 = 4
is from (1),
l31 = 3
is from (2) and
l32 = -2
is from (3)) Now, we assume Z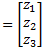
and solve LZ=C.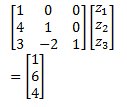
So, we have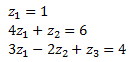
Solving, we get
z1 = 1
z2 = 2
and
z3 = 5
Now, we solve ∪X = Z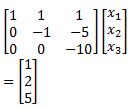
Therefore, we get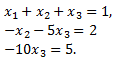
Thus, the solution to the given system of linear equations is
and hence the matrix X =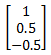
Properties
- Matrix LLL has ones on its diagonal and represents the row operations used to transform AAA into UUU.
- Matrix UUU is upper triangular and is derived from AAA after the row operations.
Applications
- Solving linear equations: Once decomposed, solving becomes easier using forward and backward substitution with L and U.
- Matrix inversion: A−1 = U−1L−1 where U−1 and L−1 are the inverses of U and L, respectively.
- Determinants: det(A) = det(L)⋅det(U).
|
34 videos|117 docs|72 tests
|
FAQs on LU Decomposition - Engineering Mathematics for Computer Science Engineering - Computer Science Engineering (CSE)
| 1. What is LU Decomposition in computer science engineering? |  |
| 2. What is the main purpose of using LU Decomposition in numerical analysis? |  |
| 3. How is LU Decomposition different from other matrix factorization methods? |  |
| 4. Can LU Decomposition be used for solving large systems of linear equations efficiently? |  |
| 5. What are some common applications of LU Decomposition in computer science engineering? |  |
|
34 videos|117 docs|72 tests
|

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|



















