Directional Derivatives | Engineering Mathematics for Electrical Engineering - Electrical Engineering (EE) PDF Download
What is a Directional Derivative?
Directional derivative provides valuable information about how a function changes concerning specific directions in space, making it useful in various fields such as physics, engineering, and economics.Directional Derivative Definition
A directional derivative is a derivative of a function in the direction of a specified vector. It measures how the function changes as you move along a particular direction in its domain.Directional Derivative Formula
Calculating the directional derivative involves the dot product of the gradient and the direction vector. In simple terms, for a function f, the directional derivative Dv(f) is given by:where:
- ∇f represents Gradient of Function
- v is Direction Vector Along which we Want to Find Derivative
How to Calculate Directional Derivative
To calculate the directional derivative of a function at a given point in a specific direction, follow these steps:Step 1: Find the Gradient
Compute the gradient (∇f) of the function. The gradient is a vector that points in the direction of the steepest increase of the function.
Step 2: Normalize Direction Vector
Normalize the direction vector (v) to ensure it has a length of 1. This is done by dividing each component of the vector by its magnitude.
Step 3: Dot Product
Take the dot product of the normalized direction vector and the gradient. The dot product is obtained by multiplying corresponding components of the two vectors and then summing them up.
Dv(f) =∇f⋅v
Step 4: Evaluate at a Point: Plug in the coordinates of the point where you want to find the directional derivative into the gradient and the normalized direction vector.
Dv(f)(a, b) = ∇f(a, b)⋅v
Directional Derivative Formula in Vector Calculus
In three dimensions or vector calculus, the directional derivative measures how a function changes along a specific direction in space. Mathematically, it is denoted as ∇vf or Dv(f), where f is the function and v is the direction vector.The directional derivative in three dimensions is computed using the dot product between the gradient of the function and the normalized direction vector:
∇vf = ∇f⋅v
where:
- ∇f represents Gradient of Function
- v is Unit Vector Indicating Direction in which Derivative is to be Calculated
Directional Derivative in Different Coordinate Systems: Directional derivatives help in analyzing how functions change along specific directions at given points, and they are applicable in various coordinate systems such as Cartesian, cylindrical, and spherical coordinates.
Directional Derivative in Cartesian Coordinates: In Cartesian coordinates, directional derivatives are calculated using the gradient operator (∇), which is a vector representing the rate of change of a scalar function in each coordinate direction. For a function f(x, y, z), the directional derivative in the direction of a unit vector u = (u1, u2, u3) at a point P(x0, y0, z0) is given by the dot product of the gradient of (f) and (u):
Duf = ∇ f · u
Directional Derivative in Cylindrical Coordinates: In cylindrical coordinates (ρ, ϕ, z), where (ρ) represents the radial distance, (ϕ) the azimuthal angle, and (z) the vertical position, directional derivatives are computed by transforming the gradient operator (∇) to cylindrical coordinates. The directional derivative in the direction of a unit vector u = (uρ, uϕ, uz) at a point P(ρ0, ϕ0, z0) is given by:
Duf = ∇ f · u
Directional Derivative in Spherical Coordinates: In spherical coordinates (r, θ, ϕ), (r) represents the radial distance, (θ) the polar angle, and (ϕ) the azimuthal angle, directional derivatives are similarly computed using the gradient operator (∇) transformed to spherical coordinates. The directional derivative in the direction of a unit vector u = (ur, uθ, uϕ) at a point P(r0, θ0, ϕ0) is given by:
Duf = ∇ f · u
Properties of Directional Derivative
Directional derivatives possess certain properties that can be described as follows:Rule for Constant Factor: If we have a constant (k), then the directional derivative of (kf) in the direction of (v) is given by (k) times the directional derivative of (f) in the same direction.
∇v(kf) = k ∇vf
∇v(f + g) = ∇vf + ∇vg
Rule for Product (Leibniz’s Rule): For the product of two functions (f) and (g), the directional derivative in the direction of (v) is given by the product of the directional derivative of one function and the other function, plus the product of the original functions with their respective directional derivatives.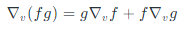 Chain Rule: When applying the chain rule, if (f) is differentiable at point (a) and (g) is differentiable at f(a), then the directional derivative of their composition is the product of the derivative of the outer function evaluated at the inner function’s value and the directional derivative of the inner function.
Chain Rule: When applying the chain rule, if (f) is differentiable at point (a) and (g) is differentiable at f(a), then the directional derivative of their composition is the product of the derivative of the outer function evaluated at the inner function’s value and the directional derivative of the inner function.
Linearity and Directional Derivative
Linearity in the context of directional derivatives refers to the property where the directional derivative of a linear combination of functions is equal to the same linear combination of their directional derivatives. Mathematically, this can be expressed as follows:
Let f and g be differentiable functions defined in a neighborhood of a point a, and let k1 and k2 be constants. Then, the directional derivative of k1f+k2g in the direction of v can be written as:
∇v(k1f + k2g) = k1∇vf + k2∇vg
This property essentially states that the directional derivative behaves linearly with respect to linear combinations of functions. It’s a fundamental property that allows for easier computation and understanding of how directional derivatives behave under combinations of functions.
Directional Derivative Gradient
Gradient for the function f(x,y) is defined as:
▽f = ▽f(x, y) = ∂f/∂xi + ∂f/∂yj
Directional derivative of the function is calculated by taking the dot product of the gradient and the given unit vector. For a function f(x, y, z) and unit vector u(u1, u2, u3) then is directional derivative gradient is calculated as:
Duf = ▽f.u = ∂f/∂x u1 + ∂f/∂y u2 + ∂f/∂z u3
Difference Between Directional Derivative and Partial Derivative
Difference between directional derivative and partial derivative can be understood from the table below: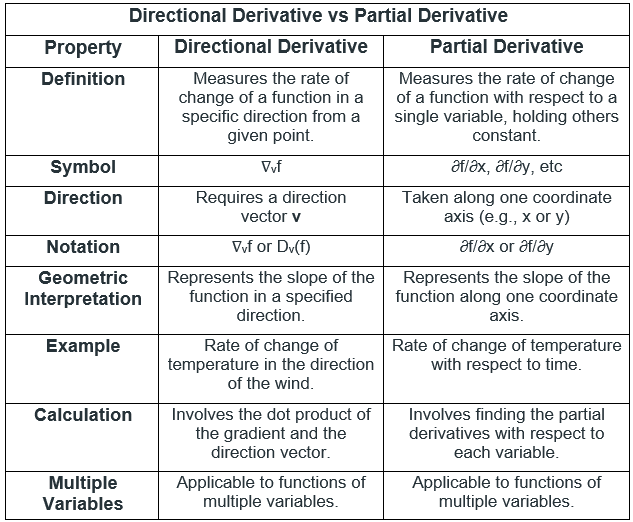
|
44 videos|109 docs|58 tests
|





















