Solution of a Sequencing Problem | Industrial Engineering - Mechanical Engineering PDF Download
| Table of contents |

|
| Introduction |

|
| Processing of n jobs through two machines |

|
| Processing of n Jobs through Three Machines |

|
| Problems with n Jobs and m Machines |

|
Introduction
When multiple jobs need to be processed on two or more machines, a manager's primary concern is determining the optimal order or sequence for performing these jobs. This introduction will address sequencing problems within a factory setting and explore methods for their solution. Sequencing problems can generally be divided into two categories. In the first category, there are n jobs, each requiring processing on some or all of k different machines. We can assess the effectiveness of each sequence that is technologically feasible (i.e., sequences that meet the restrictions on the order in which each job must be processed through the machines) and choose the sequence that optimizes effectiveness. For instance, given the processing times of each of the n jobs on each of the k machines in a specific order, the measure of effectiveness might be the total time required to complete all jobs. We aim to select sequences that minimize the total processing time across all machines.
In this unit, we will explore solutions to sequencing problems, discussing the following scenarios:
a) n jobs and two machines, A and B, with all jobs processed in the order AB.
b) n jobs and three machines, A, B, and C, with all jobs processed in the order ABC.
c) Problems involving n jobs and m machines.
Processing of n jobs through two machines
The simplest sequencing problem involves processing n jobs on two machines, where the goal is to determine the optimal sequence that minimizes the total elapsed time T. This problem can be described as follows:
a) Only two machines A and B are involved;
b) Each job is processed in the order AB.
c) The exact or expected processing times A1,A2,A3, --- , An ; B1,B2,B3, --- , Bn are known and are provided in the following table

The problem is to find the sequence (or order) of jobs so as to minimize the total elapsed time T. The solution of the above problem is also known as Johnsons procedure which involves the following steps:
Step 1: Select the smallest processing time occurring in the list A1, A2, A3, --- , An ; B1,B2,B3, --- , Bn if there is a tie, either of the smallest processing times can be selected.
Step 2: If the least processing time is Ar , select the rth job first. If it is Bs, do the sth job last as the given order is AB
Step 3: There are now (n-1) jobs left to be ordered. Repeat steps I and II for the remaining set of processing times obtained by deleting the processing time for both the machines corresponding to the job already assigned.
Step 4: Continue in the same manner till the entire jobs have been ordered. The resulting ordering will minimize the total elapsed time T and is called the optimal sequence.
Step 5: After finding the optimal sequence as stated above find the total elapsed time and idle times on machines A and B as under:
- Total elapsed time = The time between starting the first job in the optimal sequence on machine A and completing the last job in the optimal machine B.
- Idle time on machine A = (Time when the last job in the optimal sequence on sequences is completed on machine B)- (Time when the last job in the optimal sequences is completed on machine A)
- Idle time on machine B = (Time when the first job in the optimal sequences is completed on machine A)+

The Johnsons procedure can be illustrated by following examples:
Example 1: There are nine jobs, each of which must go through two machines P and Q in the order PQ, the processing times (in hours) are given below: Find the sequence that minimizes the total elapsed time T. Also calculate the total idle time for the machines in this period.
Find the sequence that minimizes the total elapsed time T. Also calculate the total idle time for the machines in this period.
Sol:
The minimum processing time on two machines is 2 which correspond to task A on machine P. This shows that task A will be preceding first. After assigning task A, we are left with 8 tasks on two machines Minimum processing time in this reduced problem is 3 which correspond to jobs E and G (both on machine Q). Now since the corresponding processing time of task E on machine P is less than the corresponding processing time of task G on machine Q therefore task E will be processed in the last and task G next to last. The situation will be dealt as
Minimum processing time in this reduced problem is 3 which correspond to jobs E and G (both on machine Q). Now since the corresponding processing time of task E on machine P is less than the corresponding processing time of task G on machine Q therefore task E will be processed in the last and task G next to last. The situation will be dealt as The problem now reduces to following 6 tasks on two machines with processing time as follows:
The problem now reduces to following 6 tasks on two machines with processing time as follows:
Here since the minimum processing time is 4 which occurs for tasks C and I on machine P and task D on machine Q. Therefore, the task C which has less processing time on P will be processed first and then task I and task D will be placed at the last i.e., 7th sequence cell.
The sequence will appear as follows: The problem now reduces to the following 3 tasks on two machines
The problem now reduces to the following 3 tasks on two machines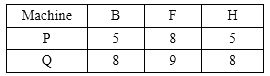 In this reduced table the minimum processing time is 5 which occurs for tasks B and H both on machine P. Now since the corresponding time of tasks B and H on machine Q are same i.e. 8. Tasks B or H may be placed arbitrarily in the 4th and 5th sequence cells. The remaining task F can then be placed in the 6th sequence cell. Thus the optimal sequences are represented as
In this reduced table the minimum processing time is 5 which occurs for tasks B and H both on machine P. Now since the corresponding time of tasks B and H on machine Q are same i.e. 8. Tasks B or H may be placed arbitrarily in the 4th and 5th sequence cells. The remaining task F can then be placed in the 6th sequence cell. Thus the optimal sequences are represented as Further, it is also possible to calculate the minimum elapsed time corresponding to the optimal sequencing A → I → C → B → H → F → D → E → G.
Further, it is also possible to calculate the minimum elapsed time corresponding to the optimal sequencing A → I → C → B → H → F → D → E → G.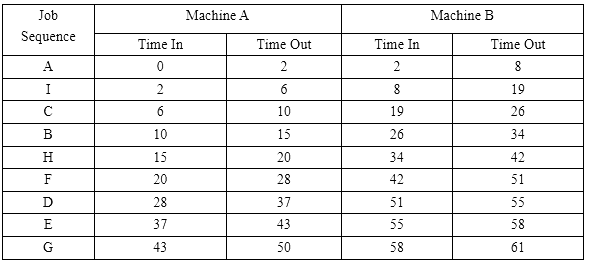
Hence the total elapsed time for this proposed sequence staring from job A to completion of job G is 61 hours .During this time machine P remains idle for 11 hours (from 50 hours to 61 hours)and the machine Q remains idle for 2 hours only (from 0 hour to 2 hour ).
Processing of n Jobs through Three Machines
The type of sequencing problem can be described as follows:
a) Only three machines A, B and C are involved;
b) Each job is processed in the prescribed order ABC
c) No passing of jobs is permitted i.e. the same order over each machine is maintained.
d) The exact or expected processing times A1,A2,A3, --- , An ; B1,B2,B3, --- , Bn and C1,C2,C3, --- , Cn are known and are denoted by the following table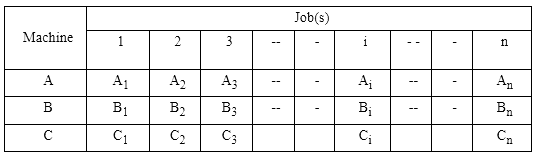
Our objective will be to find the optimal sequence of jobs which minimizes the total elapsed time. No general procedure is available so far for obtaining an optimal sequence in such case. However, the Johnsons procedure can be extended to cover the special cases where either one or both of the following conditions hold:
a) The minimum processing time on machine A ≥ the maximum processing time on machine B.
b) The minimum processing time on machine C ≥ the maximum processing time on machine B.
The method is to replace the problem by an equivalent problem involving n jobs and two machines. These two fictitious machines are denoted by G and H and the corresponding time Gi and Hi are defined by
Gi = Ai + Bi and Bi + Ci
Now this problem with prescribed ordering GH is solved by the method with n jobs through two machines, the resulting sequence will also be optimal for the original problem. The above methodology is illustrated by following example:
Example 2: There are five jobs (namely 1,2,3,4 and 5), each of which must go through machines A, B and C in the order ABC. Processing Time (in hours) are given below: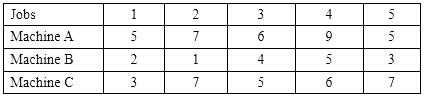
Find the sequence that minimum the total elapsed time required to complete the jobs.
Sol:
Here Min Ai = 5; Bi = 5 and Ci =3 since the condition of Min. Ai ≥ Max. Bi is satisfied the given problem can be converted into five jobs and two machines problem.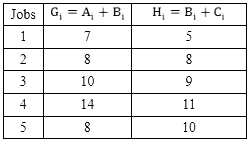
The Optimal Sequence will be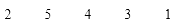
Total elapsed Time will be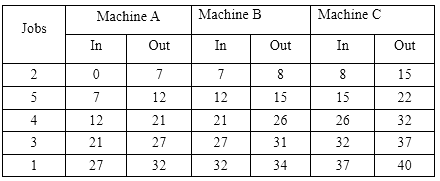 Min. total elapsed time is 40 hours.
Min. total elapsed time is 40 hours.
Idle time for Machine A is 8 hrs. (32-40)
Idle time for Machine B is 25 hours (0-7, 8-12, 15-21, 26-27, 31-32 and 34-40)
Idle time for Machine C is 12 hours (0-8, 22-26.)
Problems with n Jobs and m Machines
Let there be n jobs, each of which is to be processed through m machines, say M1,M2, --- , Mm in the order M1,M2,M3, --- , Mm. Let Tij be the time taken by the ith machine to complete the jth job.
The iterative procedure of obtaining an optimal sequence is as follows:
Step I: Find (i) minj (T1j) ii) minj (Tmj) iii) maxj (T2j,T3j,T4j, --- , T(m-1)j) for j = 1,2,---, n
Step II: Check whether
a. minj(T1j) ≥ maxj (Tij) for i = 2,3,----,m-1
Or
b. minj(Tmj) ≥ maxj (Tij) for i = 2,3,---,m-1
Step III: If the inequalities in Step II are not satisfied, method fails, otherwise, go to next step.
Step IV: Convert the m machine problem into two machine problem by introducing two fictitious machines G and H, such that
TGj = T1j + T2j + --- +T(m-1)j and THj = T2j + T3j + --- +Tmj
Determine the optimal sequence of n jobs through 2 machines by using optimal sequence algorithm.
Step V: In addition to condition given in Step IV, if Tij = T2j + T3j + --- +Tmj = C is a fixed positive constant for all i = 1, 2, 3, , n then determine the optimal sequence of n jobs and two machines M1 and Mm in the order M1Mm by using the optimal sequence algorithm.
Example 3: Find an optimal sequence for the following sequencing problem of four jobs and five machines when passing is not allowed, of which processing time (in hours) is given below: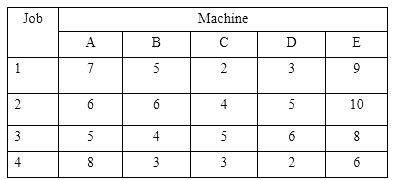 Also find the total elapsed time.
Also find the total elapsed time.
Sol:
Here Min. Ai = 5, Min. Ei = 6
Max. (Bi, Ci, Di) = 6, 5, 6respectively
Since Min. Ei = Max. (Bi, Di) and Min. Ai = Max. Ci satisfied therefore the problem can be converted into 4 jobs and 2 fictitious machines G and H as follows: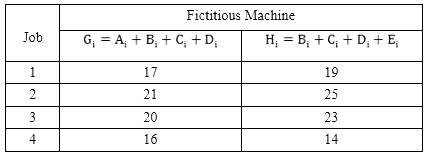 The above sequence will be:
The above sequence will be:
Total Elapsed Time Corresponding to Optimal Sequence can be obtained as follows: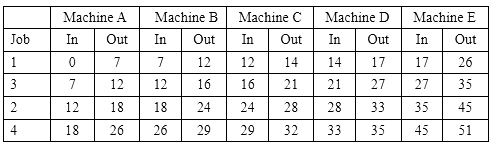
Thus the minimum elapsed time is 51 hours.
- Idle time for machine A = 25 hours(26-51)
- Idle time for machine B = 33 hours(0-7,16-18,24-26,29-51)
- Idle time for machine C = 37 hours(0-12,14-16,21-24,28-29,32-51)
- Idle time for machine D = 35 hours (0-14,17-21,27-28,35-51)
- Idle time for machine E = 18 hours (0-17,26-27)
|
30 videos|64 docs|30 tests
|
FAQs on Solution of a Sequencing Problem - Industrial Engineering - Mechanical Engineering
| 1. What is the significance of sequencing in mechanical engineering? |  |
| 2. How does the processing of n jobs through two machines differ from three machines? |  |
| 3. What are some common problems encountered when dealing with n jobs and m machines in manufacturing? |  |
| 4. What are some common solutions to sequencing problems in mechanical engineering? |  |
| 5. How can sequencing problems impact the overall performance of a manufacturing system? |  |




















