Cauchy’s integral theorem and integral formula | Engineering Mathematics for Electrical Engineering - Electrical Engineering (EE) PDF Download
| Table of contents |

|
| Cauchy’s Integral Formula |

|
| Cauchy’s Integral Theorem |

|
| Generalisation of Cauchy’s Integral Formula |

|
| Solved Numericals |

|
Cauchy’s Integral Formula
Cauchy's integral formula is a fundamental result in complex analysis, a branch of mathematics. It asserts that a holomorphic function defined on a disk is completely determined by its values on the boundary of the disk. This formula provides integral representations for all derivatives of a holomorphic function. Named after Augustin-Louis Cauchy, this theorem is a cornerstone of complex analysis.Simply Connected Region
A region is termed as simply connected if, for any closed curve C within the region, all points inside C are also contained within the region. This implies that the region has no holes or isolated boundary points.
Cauchy’s Integral Theorem
Statement: If f(z) is an analytic function in a simply-connected region R, then ∫c f(z) dz = 0 for every closed contour c contained in R.If f(z) is an analytic function and its derivative f'(z) is continuous at all points within and on a simple closed curve C, then ∫c f(z) dz = 0.
Cauchy’s Integral Formula
If a complex function f(z) is analytic within and on a closed contour c inside a simply-connected domain, and if z0 is any point in the middle of C, then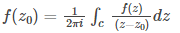 Here, the integral should be taken in the positive sense around c.
Here, the integral should be taken in the positive sense around c.Generalisation of Cauchy’s Integral Formula
If f(z) is an analytic function within and on a simple closed curve C and if z0 is any point within c, then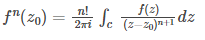 Converse of Cauchy’s Integral Theorem
Converse of Cauchy’s Integral TheoremIf a complex function f(z) is continuous throughout the simple connected domain D and if ∫c f(z) dz = 0 for every closed contour c in D, then f(z) will be an analytic function in D.
This theorem is also known as Morera’s theorem.
Solved Numericals
Q1. The value of the integral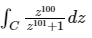 where C is the circle of radius 2 centred at the origin taken in the anti-clockwise direction is:
where C is the circle of radius 2 centred at the origin taken in the anti-clockwise direction is:Solution:
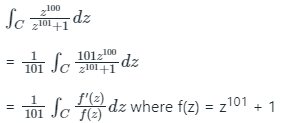
f(z) is a polynomial of degree 101 so number of zeros of f(z) is 101
Hence using Cauchy's argument principle,
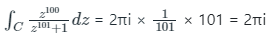
Q2. What is the value of 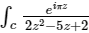 , where C is the circle |z| = 1 is with positive orientation.
, where C is the circle |z| = 1 is with positive orientation.
Solution: Given,
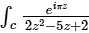
C is the circle |z| = 1 is with positive orientation
Let f(z) = 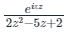
Putting 2z2 - 5z + 2 = 0
⇒ 2z2 - 4z - z + 2 = 0
⇒ 2z(z - 2) - 1(z - 2) = 0
⇒ (z - 2)(2z - 1) = 0
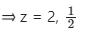
Now z = 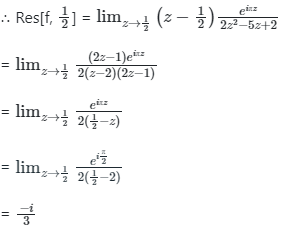
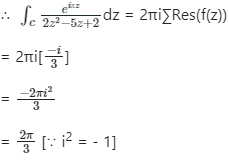
∴ The value of the given integral is 2π/3.
Q3. The value of 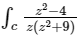 is where C is a circle |z| = 1,
is where C is a circle |z| = 1,
Solution: Given,

C is a circle, lzl=1
Let f(z) = 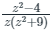
Putting z(z2 + 9) = 0
⇒ z = 0, 3i, - 3i
Now, z = 0 lies inside C.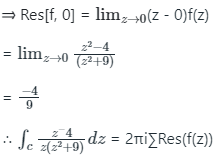
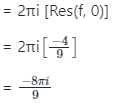
∴ The value of given integral is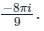
Q4. Let γ be the positively oriented circle in the complex plane given by {z ∈ ℂ: |z – 1| = 1}. Then 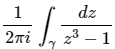 equals:
equals:
Solution: Given,
Let γ be the positively oriented circle in the complex plane given by {z ∈ ℂ: |z – 1| = 1}. Then 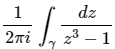
Cauchy Integral Formula -
Let f(z) be analytic in a region D and let C be a closed curve in D. If a is any point in D, then
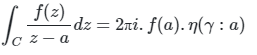
here 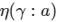 is a winding number. The winding number measures the number of times a path (counter-clockwise) winds around a point.
is a winding number. The winding number measures the number of times a path (counter-clockwise) winds around a point.
We have γ = {z ∈ ℂ: |z – 1| = 1}.
Now using Cauchy Integral formula we get -
|
44 videos|109 docs|58 tests
|
FAQs on Cauchy’s integral theorem and integral formula - Engineering Mathematics for Electrical Engineering - Electrical Engineering (EE)
| 1. What is Cauchy’s Integral Formula? |  |
| 2. How is Cauchy’s Integral Formula different from Cauchy’s Integral Theorem? |  |
| 3. What is the significance of Cauchy’s Integral Formula in Mechanical Engineering? |  |
| 4. How is Cauchy’s Integral Formula applied in real-world engineering problems? |  |
| 5. What are some common misconceptions about Cauchy’s Integral Formula and Theorem? |  |




















