Numerical solutions of linear and nonlinear algebraic equations | Engineering Mathematics for Mechanical Engineering PDF Download
Solved Numericals
Q1. If a and (a + h) are two consecutive approximate roots of the equation f(x) = 0 obtained by Newton's method, then h is equal to.
Solution: Given, a and (a + h) are two consecutive approximate roots of the equation f(x) = 0
Let xn = a and xn+1 = a + h
∴ Using Newton's method, 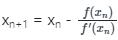
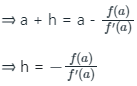
∴ The value of h is 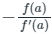 .
.
Q2. While solving the equation x2 – 3x + 1 = 0 using Newton – Raphson method the initial guess of the root is as 1, then the value of the root will be?
Solution: Given, f(x) = x2 – 3x + 1 and x0 = 1
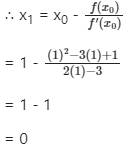
∴ The value of root will be x = 0.
Q3. The iterative formula to find the root of the equation f(x) = x3 - 5x + 7 = 0 by the Newton Raphson method is ______.
Solution: Given,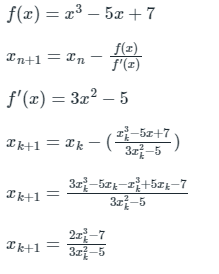
Q4. If f(0) = 3, f(1) = 5, f(3) = 21, then the unique polynomial of degree 2 or less using Newton divided difference interpolation will be:
Solution: Given,
f(0) = 3, f(1) = 5, f(3) = 21;
⇒ (0,3), (1,5), (3,21) are the data points;
The polynomial will be f(x) = b0 + b1(x) + b2 (x)(x – 1);
⇒ b0 = f(0) = 3;
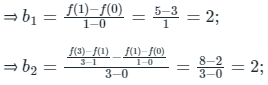
Substituting the constant b0, b1, b2 in the quadratic interpolant,
⇒ f(x) = 3 + 2x + 2 (x)(x – 1) = 3 + 2x + 2x2 – 2x = 3 + 2x2;
The unique polynomial of degree 2 will be f(x) = 3 + 2x2.
Q5. The 2nd approximation to a root of the equation x2 - x - 1 = 0 in the interval (1, 2) by Bisection method will be:
Solution: Given:
f(x) = x2 - x - 1 = 0 , a = 1 , b = 2
f(1) = 1 - 1 -1 = -1 < 0 , f(2) = 22 - 2 - 1 = 1 > 0 , Hence root lies between 1 and 2
By Bi-section method, 
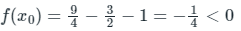
Which is positive. Hence, the root lies between 1.5 and 2
By Bi-section method, 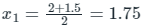
The 2nd approximation to a root of the equation x2 - x - 1 = 0 in the interval (1, 2) by Bisection method is 1.75
Q6. The approximate value of a root of x3 – 13 = 0, then 3.5 as initial value, after one iteration using Newton-Raphson method, is
Solution: Given:
f(x) = x3 - 13, x0 = 3.5
f'(x) = 3x2
f(x0) = f(3.5) = 3.53 - 13 = 29.875
f'(x0) = f'(3.5) = 3 × 3.52 = 36.75
We know that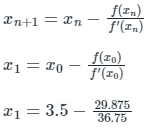
∴ x1 = 2.6871
Q7. The iterative formula to find the root of the equation f(x) = x3 - 5x + 7 = 0 by the Newton Raphson method is ______.
Solution: Given,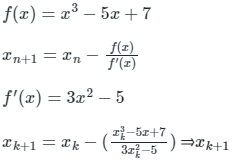
= 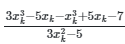
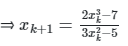
Q8. Find the positive real root of x3 - x - 3 = 0 using Newton-Raphson method. If the starting guess (x0) is 2, the numerical value of the root after two iterations (x2) is __________ (round off to two decimal places).
Ans: 1.66 - 1.68
Solution:
f(x) = x3 - x - 3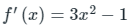
Starting guess (x0 = 2)
Now first iterations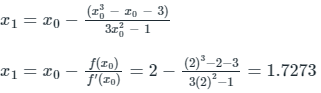
Second iterations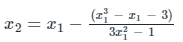
x1 = 1.7273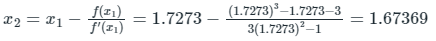
x2 = 1.67
Q9. The function f(x) = ex – 1 is to be solved using Newton-Raphson method. If the initial value of x0 is taken as 1.0, then the absolute error Ans: 0.05 - 0.07
Solution:
f(x) = ex – 1
f’(x) = ex
x0 = 1
Iteration 1:
At x0 = 1, f(x) = 1.718
f'(x) = 2.718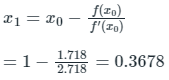
Iteration 2:
At x2 = 0.3678, f(x) = 0.4445
f'(x) = 1.4445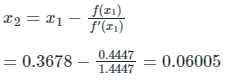
By inspection, the actual solution for the given equation is, x = 0
Therefore, the error = 0.06005.
Q10. The iteration formula to find the reciprocal of a given number N by Newton’s method is
Solution: Given, X = 1/N
Let, 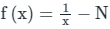
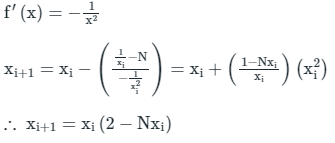
Q11. If the equation sin (x) = x2 is solved by Newton Raphson’s method with the initial guess of x = 1, then the value of x after 2 iterations would be
Ans: 0.86 - 0.89
Solution: Given:
Initial guess (x0) = 1; sin(x) = x2 ⇒ f(x) = x2 - sin(x);
f'(x) = 2x - cos(x)
First iteration (n = 0)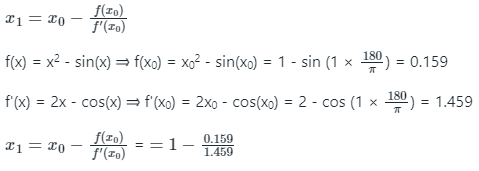
x1 = 0.891
Second Iteration (n = 1)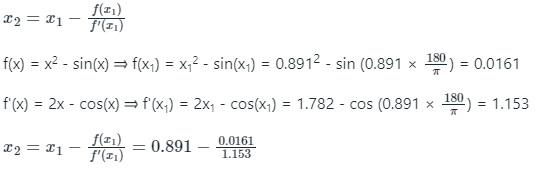
x2 = 0.87
|
53 videos|114 docs|63 tests
|
FAQs on Numerical solutions of linear and nonlinear algebraic equations - Engineering Mathematics for Mechanical Engineering
| 1. What are numerical solutions of linear algebraic equations? |  |
| 2. How are nonlinear algebraic equations solved using numerical methods? |  |
| 3. What is the importance of solving algebraic equations in Mechanical Engineering? |  |
| 4. What are some common challenges faced when solving algebraic equations numerically? |  |
| 5. Can numerical solutions of algebraic equations be used in real-world engineering applications? |  |
















