Open App

SSC CGL Exam > SSC CGL Notes > Quantitative Aptitude for SSC CGL > Quadrilateral: Overview and Examples

Quadrilateral: Overview and Examples | Quantitative Aptitude for SSC CGL PDF Download

Table of contents
Quadrilateral
Types of Quadrilaterals
Quadrilateral Formula
Perimeter of Quadrilateral
Area of Quadrilateral
Sides and Angles of Quadrilaterals

Any four points that don't lie on the same line make a quadrilateral; this shape goes by different names based on its form. A quadrilateral is a flat geometric figure with four sides and four corners. Understanding quadrilaterals is essential for various exams like SSC, Railways, AAI, and academic tests. A quadrilateral encompasses shapes like parallelograms, rectangles, squares, rhombuses, trapeziums, and kites, each with unique properties and formulas. These geometric concepts are crucial for competitive exams and academic studies.

Quadrilateral

In geometry, a quadrilateral is a shape with four sides, four angles, and four vertices. It's formed by connecting four points where any three points are not in a straight line. Several types of quadrilaterals exist, including a square, rectangle, parallelogram, rhombus, trapezium, and kite. We'll explore each type in the sections ahead.

Types of Quadrilaterals

The term Quadrilateral originates from a Latin term, where Quadra signifies four and Latus means sides. A quadrilateral can have four sides that are either the same or different. Examples of quadrilaterals include rectangle, square, trapezoid, and kite, which typically exhibit a four-sided structure.

Various types of quadrilaterals are elaborated upon below:

Parallelogram

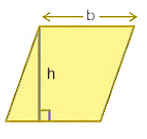
Definition: A quadrilateral with two pairs of opposite sides that are parallel and equal in length.

Properties:

Opposite sides are parallel (AB || CD, BC || AD).
Opposite sides are equal in length (AB = CD, BC = AD).
Diagonals bisect each other.
The sum of any two adjacent angles is 180 degrees (∠A + ∠B = 180°, ∠B + ∠C = 180°, etc.).

Rectangle

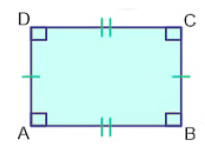
Quadrilateral: Overview and Examples | Quantitative Aptitude for SSC CGL

Definition: A parallelogram where each angle measures 90 degrees.

Properties:

Opposite sides are parallel (AB || CD, BC || AD).
Opposite sides are equal in length (AB = CD, BC = AD).
All angles are equal to 90 degrees (∠A = ∠B = ∠C = ∠D = 90°).
Diagonals bisect each other and are equal in length.

Square

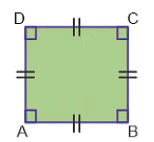
Definition: A parallelogram with all sides equal and each angle measuring 90 degrees.

Properties:

All sides are equal in length (AB = BC = CD = DA).
Opposite sides are parallel (AB || CD, BC || AD).
All angles are equal to 90 degrees (∠A = ∠B = ∠C = ∠D = 90°).
Diagonals bisect each other at right angles and are equal in length.

Rhombus

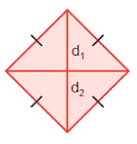
Definition: A parallelogram where all sides are equal, and the diagonals bisect each other at right angles.

Properties:

All sides are equal in length (AB = BC = CD = DA).
Opposite sides are parallel (AB || CD, BC || AD).
Opposite angles are equal.
Diagonals bisect each other perpendicularly.

Trapezium

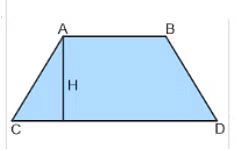Definition: A quadrilateral with only one pair of opposite sides that are parallel.

Properties:

Only one pair of opposite sides are parallel (AB || CD).
The non-parallel sides are called the legs of the trapezium.
The diagonals do not bisect each other in the same ratio.

Kite

Definition: A quadrilateral with two pairs of adjacent sides that are equal in length.

Properties:

Two pairs of adjacent sides are equal (AB = AD, BC = CD).
The diagonals intersect at right angles.
One of the diagonals bisects the other.

Quadrilateral Formula

Shapes: We previously talked about square, rectangle, parallelogram, rhombus, trapezium, and kite with a detailed illustration.
Formulas: Let's now understand the fundamental equations connected to these shapes. Area and perimeter represent the basic formulas for different four-sided figures. The following are the formulas:
- Area: The space inside a shape.
- Perimeter: The total length of the boundary of a shape.

Perimeter of Quadrilateral

The perimeter refers to the total distance around the edge of any flat shape.
In a four-sided shape (quadrilateral), the perimeter is the sum of all four side lengths.
Various types of quadrilaterals have different perimeters.

Note: The perimeter is the total distance around the edge of a 2D shape, like a square or rectangle. For a quadrilateral, which is a shape with four sides, the perimeter is the sum of all four side lengths. Different types of quadrilaterals have different perimeters based on their side measurements.

Shape	Formula for Perimeter
Parallellogram	2 × (sum of lengths of adjacent sides). 2 × (Base + Side)
Rectangle	2 x (L + B) = 2 × (Length + Breadth)
Square	2 × (a + a) = 4a (4 times the side length)
Rhombus	4x (where x is a side)
Trapezium	Sum of lengths of all the sides
Kite	2 x (side length one + side length two) 2 (x + y) (where, x and y denote adjacent pairs

Area of Quadrilateral

The area of a four-sided shape is the total space it takes up. Here are the area formulas for different shapes:

Square: All sides are equal. Area = side x side
Parallelogram: Opposite sides are parallel. Area = base x height
Rectangle: Opposite sides are equal and all angles are 90 degrees. Area = length x width
Rhombus: All sides are equal, opposite angles are equal. Area = (diagonal1 x diagonal2) / 2
Trapezium: One pair of parallel sides. Area = 0.5 x (sum of parallel sides) x height
Kite: Two pairs of adjacent sides are equal. Area = 0.5 x (diagonal1 x diagonal2)

Shape	Area
Parallelogram	b × h (base × height)
Rectangle	Length × Breadth ( L × B)
Square	$a^{2}$ (side length squared)
Rhombus	$\frac{1}{2} \times d_{1} \times d_{2}$ (where length of two diagonals of the is $d_{1} and d_{2}$ )
Trapezium	$\frac{1}{2} \times (Addition of lengths of parallel sides) \times h$ (where, ‘h’ represents the height)
Kite	$\frac{1}{2} \times {Diagonal}_{1} \times {Diagonal}_{2}$

Sides and Angles of Quadrilaterals

Learn about key facts on sides and angles of parallelogram, rectangle, square, rhombus, and trapezium.

Opposite sides run alongside each other and look the same with lines from corner to corner cutting each other into two.
The angles have different measurements, but the opposite angles are of the same size.

Shape

Sides

Angles

Parallelogram

Opposite sides run alongside each other and look the same with lines from corner to corner cutting each other into two.

The opposite angles in a parallelogram are equal. Also, the summation of two adjacent angles is 180 degrees

Rectangle

Opposite sides are parallel and equivalent with diagonals bisecting each other

All angles in a rectangle are equal.
The total of adjacent angles in a rectangle equals 180 degrees.

Square

All sides of a shape are the same length.
Opposite sides run parallel to each other.
Diagonals cut each other exactly in half.

In a square, all angles are equal at 90 degrees.
Additionally, the sum of adjacent angles equals 180 degrees.

Rhombus

All the four sides are equal and the opposite side is parallel to one another with diagonals bisecting one another.

The angles have different measurements, but the opposite angles are of the same size.

Trapezium

All sides are of different lengths in such a way that one pair of opposite sides is parallel.

–

Isosceles trapezium

The non-parallel sides are of identical length

–

Properties of Quadrilaterals

Common Properties of Quadrilaterals:

Quadrilaterals have four sides.
Quadrilaterals have four vertices.
Quadrilaterals have two diagonals.
The total of all interior angles is 360 degrees.

Properties of Each Type of Quadrilateral:

Rectangle
Parallelogram
Rhombus
Square
Trapezoid
Kite

Shape	Properties
Square	Every side of the square is of the same length. The sides of a square run parallel to each other. All the inside angles of a square are right angles (90 degrees). The diagonals of a square intersect each other at right angles.
Rectangle	The sides of a rectangle that face each other have the same length. The sides of a rectangle that face each other are parallel. All the inside corners are right angles (90 degrees). The lines that go from one corner of a rectangle to the opposite corner cross each other in the middle.
Rhombus	All sides of a rhombus are of the same length. Opposite sides of the rhombus run parallel to each other. Opposite angles are of the same size. The total of any two adjacent angles in a rhombus equals 180 degrees. The diagonals intersect each other at right angles.
Parallelogram	Opposite sides of a parallelogram have the same size. Opposite sides run in the same direction and never meet. The lines connecting opposite corners of a parallelogram cut each other in half. The angles facing each other on opposite sides are equal. The sum of two angles next to each other in a parallelogram equals 180 degrees.
Trapezium	Only one pair of opposite sides in a trapezium run parallel to each other. The two sides next to each other in a trapezium together form a straight line, totaling 180 degrees. The diagonals of a trapezium cut each other neatly into equal parts.
Kite	Pair of adjacent surfaces of a kite have the same size. The longest diagonal of a kite divides the shortest one. Only one pair of opposite angles are the same size.

Solved Examples on Quadrilateral

A polygon is a flat shape with many sides. For instance, a shape with three sides is called a 3-gon, and one with four sides is known as a 4-gon.
This article focuses on quadrilaterals, which are polygons with four sides. The total angles inside a quadrilateral add up to 360 degrees.
Here are some solved examples of quadrilaterals.

Example 1 : Obtain the perimeter of the quadrilateral with sides 6 cm, 7 cm, 8 cm and 13 cm.

Quadrilateral: Overview and Examples | Quantitative Aptitude for SSC CGL

View Answer

Solution: Given, the measures of 4 different sides are 6 cm, 7 cm, 8 cm, and 13 cm.

As known to us the perimeter will be equivalent to the summation of the length of all four sides. That is:
P(perimeter)= 6 cm+7 cm+8 cm + 13 cm= 34 cm

Example 2 : If the two diagonals of a kite are of length 22 cm and 6 cm then what is the respective area.

View Answer

Solution: The area of a Kite= $\frac{1}{2} \times {Diagonal}_{1} \times {Diagonal}_{2}$
$\frac{1}{2} \times D_{1} \times D_{2} = \frac{1}{2} \times 22 \times 6$

Hence, the area of a Kite=66 square metres.

Example 3 :Determine the perimeter of the parallelogram whose opposite sides are 13 cm and 6 cm respectively.

View Answer

Solution: As per the property of a parallelogram, the opposite sides have identical lengths. Thus,

Perimeter = 13 cm + 6 cm + 13 cm + 6 cm = 38 cm

Example 4 : What is the base of a rectangle having an area of 72 square units and the height is 8 units.

View Answer

Solution:

Given data:

Area = 72 square units
Height = 8 units
Area of rectangle = Base × Height
72 = Base × 8
Base = 72/8 = 9 units

The document Quadrilateral: Overview and Examples | Quantitative Aptitude for SSC CGL is a part of the SSC CGL Course Quantitative Aptitude for SSC CGL.

All you need of SSC CGL at this link: SSC CGL

	Quantitative Aptitude for SSC CGL 314 videos\|170 docs\|185 tests

Quantitative Aptitude for SSC CGL

314 videos|170 docs|185 tests

Join Course for Free

Top Courses for SSC CGL

View all

FAQs on Quadrilateral: Overview and Examples - Quantitative Aptitude for SSC CGL

1. What are the different types of quadrilaterals?

Ans. The different types of quadrilaterals include parallelograms, rectangles, squares, rhombuses, trapezoids, and kites.

2. What is the formula to find the perimeter of a quadrilateral?

Ans. The formula to find the perimeter of a quadrilateral is to add up the lengths of all four sides of the quadrilateral.

3. How do you calculate the area of a quadrilateral?

Ans. The area of a quadrilateral can be calculated by using various formulas depending on the type of quadrilateral. For example, the area of a rectangle is calculated by multiplying its length and width.

4. What is the relationship between the sides and angles of a quadrilateral?

Ans. In a quadrilateral, the sum of all interior angles is always equal to 360 degrees. The sides of a quadrilateral can vary in length and do not have a specific relationship with the angles.

5. Can a quadrilateral have equal sides and angles?

Ans. Yes, a quadrilateral can have equal sides and angles. For example, a square is a type of quadrilateral with four equal sides and four right angles.

Related Exams

SSC CGL Quant

About this Document

	4.88/5 Rating
	Nov 22, 2024 Last updated

Document Description: Quadrilateral: Overview and Examples for SSC CGL 2024 is part of Quantitative Aptitude for SSC CGL preparation. The notes and questions for Quadrilateral: Overview and Examples have been prepared according to the SSC CGL exam syllabus. Information about Quadrilateral: Overview and Examples covers topics like Quadrilateral, Types of Quadrilaterals, Quadrilateral Formula , Perimeter of Quadrilateral, Area of Quadrilateral, Sides and Angles of Quadrilaterals and Quadrilateral: Overview and Examples Example, for SSC CGL 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Quadrilateral: Overview and Examples.

Introduction of Quadrilateral: Overview and Examples in English is available as part of our Quantitative Aptitude for SSC CGL for SSC CGL & Quadrilateral: Overview and Examples in Hindi for Quantitative Aptitude for SSC CGL course. Download more important topics related with notes, lectures and mock test series for SSC CGL Exam by signing up for free. SSC CGL: Quadrilateral: Overview and Examples | Quantitative Aptitude for SSC CGL

Description

Full syllabus notes, lecture & questions for Quadrilateral: Overview and Examples | Quantitative Aptitude for SSC CGL - SSC CGL | Plus excerises question with solution to help you revise complete syllabus for Quantitative Aptitude for SSC CGL | Best notes, free PDF download

Information about Quadrilateral: Overview and Examples

In this doc you can find the meaning of Quadrilateral: Overview and Examples defined & explained in the simplest way possible. Besides explaining types of Quadrilateral: Overview and Examples theory, EduRev gives you an ample number of questions to practice Quadrilateral: Overview and Examples tests, examples and also practice SSC CGL tests

	Quantitative Aptitude for SSC CGL 314 videos\|170 docs\|185 tests

Quantitative Aptitude for SSC CGL

314 videos|170 docs|185 tests

Join Course for Free

Download as PDF

Explore Courses for SSC CGL exam

Top Courses for SSC CGL

Explore Courses

Signup for Free!

Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.

Start learning for Free

10M+ students study on EduRev

past year papers

mock tests for examination

study material

Summary

practice quizzes

Extra Questions

ppt

MCQs

Semester Notes

Quadrilateral: Overview and Examples | Quantitative Aptitude for SSC CGL

Important questions

Exam

Viva Questions

shortcuts and tricks

pdf

video lectures

Sample Paper

Previous Year Questions with Solutions

Free

Quadrilateral: Overview and Examples | Quantitative Aptitude for SSC CGL

Objective type Questions

;

Additional Information about Quadrilateral: Overview and Examples for SSC CGL Preparation

Quadrilateral: Overview and Examples Free PDF Download

The Quadrilateral: Overview and Examples is an invaluable resource that delves deep into the core of the SSC CGL exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the Quadrilateral: Overview and Examples now and kickstart your journey towards success in the SSC CGL exam.

Importance of Quadrilateral: Overview and Examples

The importance of Quadrilateral: Overview and Examples cannot be overstated, especially for SSC CGL aspirants. This document holds the key to success in the SSC CGL exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

Quadrilateral: Overview and Examples Notes

Quadrilateral: Overview and Examples Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to Quadrilateral: Overview and Examples. It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, Quadrilateral: Overview and Examples Notes on EduRev are your ultimate resource for success.

Quadrilateral: Overview and Examples SSC CGL Questions

The "Quadrilateral: Overview and Examples SSC CGL Questions" guide is a valuable resource for all aspiring students preparing for the SSC CGL exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study Quadrilateral: Overview and Examples on the App

Students of SSC CGL can study Quadrilateral: Overview and Examples alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the Quadrilateral: Overview and Examples, students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of Quadrilateral: Overview and Examples is prepared as per the latest SSC CGL syllabus.

Education Revolution

Signup to see your scores go up within 7 days!

Access 1000+ FREE Docs, Videos and Tests

Continue with Google

Takes less than 10 seconds to signup