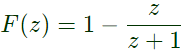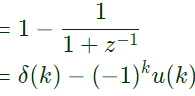Q1: If the Z-transform of a finite-duration discrete-time signal x[n] is X(z), then the Z-transform of the signal y[n] = x[2n] is (2024)
(a) Y(z) = X(z2)
(b) Y(z) = (1/2) [X(z−1/2) + X(−z−1/2)]
(c) Y(z) = (1/2) [X(z1/2)+X(−z1/2)]
(d) Y(z) = (1/2) [X(z2) + X(−z2)]
Ans: (c)
Sol:  Let
Let
2n = m
then

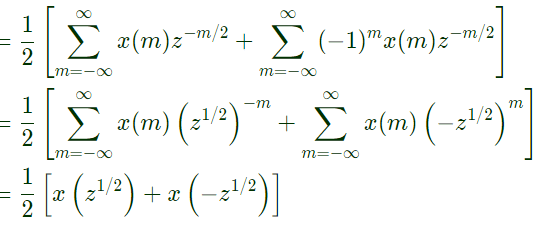
Q2: The Z-transform of a discrete signal x[n] is
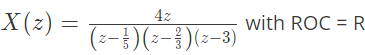 Which one of the following statements is true? (2023)
Which one of the following statements is true? (2023)
(a) Discrete-time Fourier transform of x[n] converges if R is ∣z∣ > 3
(b) Discrete-time Fourier transform of x[n] converges if R is (2/3) < ∣𝑧∣ < 3
(c) Discrete-time Fourier transform of x[n] converges if R is such that x[n] is a leftsided sequence
(d) Discrete-time Fourier transform of x[n] converges if R is such that x[n] is a rightsided sequence
Ans: (b)
Sol: Z = 1, unit circle include by ROC : (2/3) < ∣z∣ < 3.
Therefore DIFT of x[n] conveys for this ROC.
Q3: The casual signal with z-transformer Z2(Z − a)−2 is
(u[n] is the unit step signal) (2021)
(a) a2nu[n]
(b) (n + 1) anu [n]
(c) n−1 anu [n]
(d) n2anu[n]
Ans: (b)
Sol: As we know,
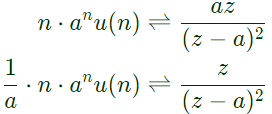
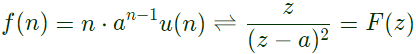 Time-shifting property,
Time-shifting property,
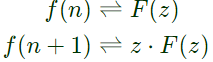
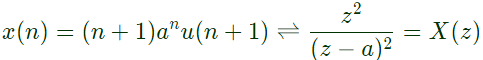 Thus,
Thus,
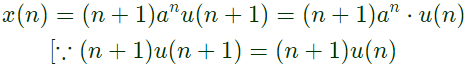
Q4: The causal realization of a system transfer function H(s) having poles at (2, -1), (-2, 1) and zeroes at (2, 1), (-2, -1) will be (2020)
(a) stable, real, allpass
(b) unstable, complex, allpass
(c) unstable, real, highpass
(d) stable, complex, lowpass
Ans: (b)
Sol: Since pole zero plot of given transfer function
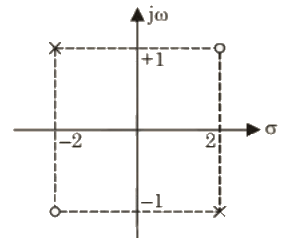 Since, given pole zero is symmetrical about origin hence it is a all pass system.
Since, given pole zero is symmetrical about origin hence it is a all pass system.
Since, one pole on the RHS thus unstable.
Since, pole doesnot have complex conjugate poles and zeros present thus system is not real means system is complex.
Q5: Consider a signal 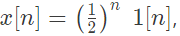 where 1[n] = 0 if n < 0, and 1[n] = 1 if n ≥ 0. The z-transform of x[n − k], k > 0 is
where 1[n] = 0 if n < 0, and 1[n] = 1 if n ≥ 0. The z-transform of x[n − k], k > 0 is 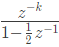 with region of convergence being (2020)
with region of convergence being (2020)
(a) ∣z∣ < 2
(b) ∣z∣ > 2
(c) ∣z∣ < 1/2
(d) ∣z∣ > 1/2
Ans: (d)
Sol: 
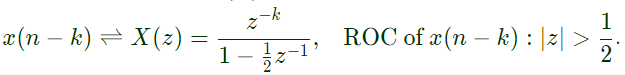
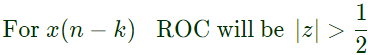
Q6: A cascade system having the impulse responses
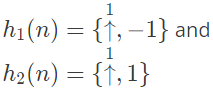 is shown in the figure below, where symbol ↑ denotes the time origin.
is shown in the figure below, where symbol ↑ denotes the time origin.
 The input sequence x(n) for which the cascade system produces an output sequence
The input sequence x(n) for which the cascade system produces an output sequence 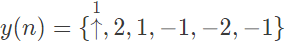 is (SET-2 (2017))
is (SET-2 (2017))
(a) 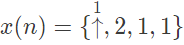
(b) 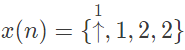
(c) 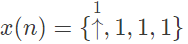
(d) 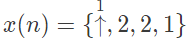
Ans: (d)
Sol: 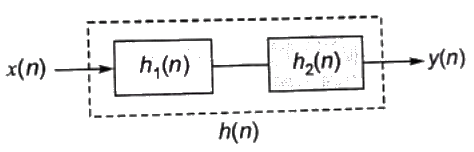 Now,
Now,
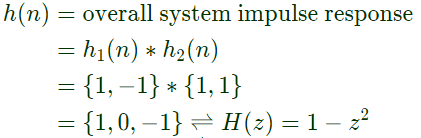
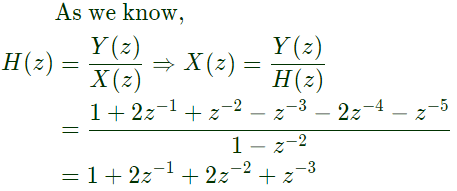
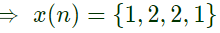
Q7: The pole-zero plots of three discrete-time systems P, Q and R on the z-plane are shown below. Which one of the following is TRUE about the frequency selectivity of these systems? (SET-2 (2017))
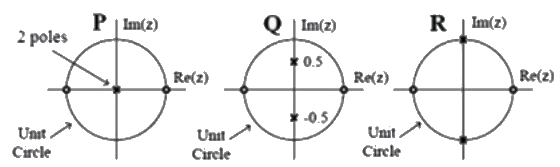 (a) All three are high-pass filters.
(a) All three are high-pass filters.
(b) All three are band-pass filters.
(c) All three are low-pass filters.
(d) P is a low-pass filter, Q is a band-pass filter and R is a high-pass filter.
Ans: (b)
Sol: Since all 3 pole-zero plots have zero at z = 1 and z = -1.
So, filter will not pass low frequency and high frequency components.
Therefore all are bandpass filter.
Note: in digital filter
For low frequency z = 1
For high frequency z = -1
Q8: Consider a causal and stable LTI system with rational transfer function H(z). Whose corresponding impulse response begins at n = 0. Furthermore, H(1) = 5/4. The poles of H(z) are 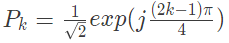 for k = 1, 2, 3, 4. The zeros of H(z) are all at z = 0. Let g[n] = jnh[n]. The value of g[8] equals ___________. (SET-1 (2017))
for k = 1, 2, 3, 4. The zeros of H(z) are all at z = 0. Let g[n] = jnh[n]. The value of g[8] equals ___________. (SET-1 (2017))
(a) 0.01
(b) 0.03
(c) 0.06
(d) 0.09
Ans: (d)
Sol: Pole locationof H(z) are given as,
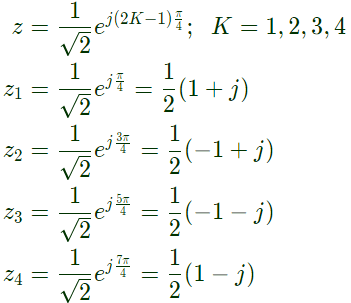 Now,
Now,
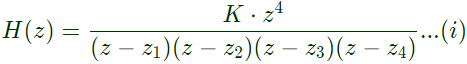 [As h(n) is causal and it starts from n=0, so numerator will have same order as denominator is having]. by solving equation (i)
[As h(n) is causal and it starts from n=0, so numerator will have same order as denominator is having]. by solving equation (i)
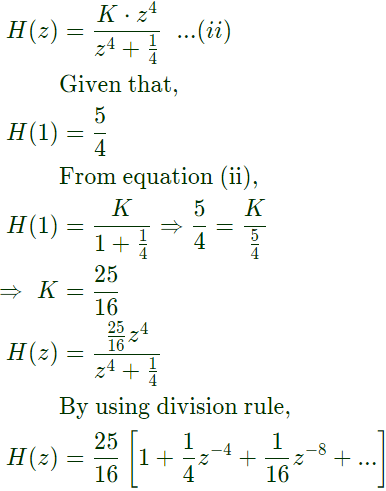
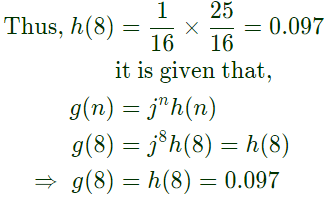
Q9: Let 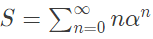 where ∣α∣ < 1. The value of α in the range 0 < α < 1, such that S = 2α is _______. (SET-1 (2016))
where ∣α∣ < 1. The value of α in the range 0 < α < 1, such that S = 2α is _______. (SET-1 (2016))
(a) 0.1
(b) 0.9
(c) 0.6
(d) 0.3
Ans: (d)
Sol: The Z-transform of
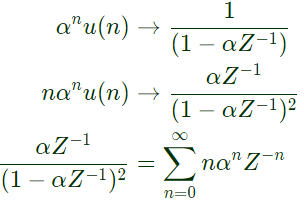 If we put Z = 1 in above equation, we get,
If we put Z = 1 in above equation, we get,
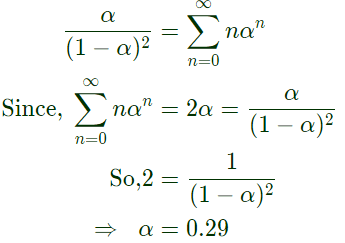
Q10: The z-Transform of a sequence x[n] is given as X(z) = 2z + 4 − (4/z) + (3/z2). If y[n] is the first difference of x[n], then Y(z) is given by (SET-2 (2015))
(a) 2z + 2 − 8/z + 7/z2 − 3/z3
(b) −2z + 2 − 6/z − 1/z2 − 3/z3
(c) −2z + 2 − 8/z − 7/z2 − 3/z3
(d) 4z − 2 − 8/z + 7/z2 − 3/z3
Ans: (a)
Sol: y(n) is first difference of x(n)
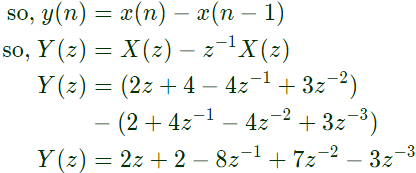
Q11: Consider a discrete time signal given by
x[n] = (−0.25)nu[n] + (0.5)nu[−n − 1]
The region of convergence of its Z-transform would be (SET-1 (2015))
(a) the region inside the circle of radius 0.5 and centered at origin
(b) the region outside the circle of radius 0.25 and centered at origin
(c) the annular region between the two circles, both centered at origin and having radii 0.25 and 0.5
(d) the entire Z plane.
Ans: (c)
Sol: x[n] = (0.25)nu(n) + (0.5)nu(−n − 1)
Signal x[n] is sum of two signals, one is right sided [(−0.25)nu(n)] and other is left sided [(0.5)nu(−n − 1)]. The right sided signal will have pole at location with magnitude 0.25. So, ROC is ∣z∣ > 0.25. The left sided signal will have pole at location with magnitude 0.5. So, ROC is ∣z∣ < 0.5. So, ROC of X(z) (Z-transform of x(n) will be ) 0.25 < ∣z∣ < 0.5.
Q12: An input signal x(t) = 2 + 5sin(100πt) is sampled with a sampling frequency of 400 Hz and applied to the system whose transfer function is represented by
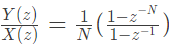 where, N represents the number of samples per cycle. The output y(n) of the system under steady state is (SET-2 (2014))
where, N represents the number of samples per cycle. The output y(n) of the system under steady state is (SET-2 (2014))
(a) 0
(b) 1
(c) 2
(d) 5
Ans: (c)
Sol: 
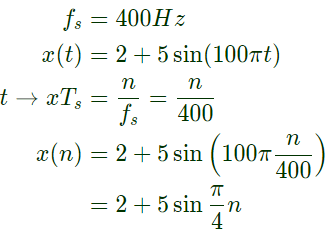
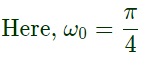 Therefore, N = time-period of
Therefore, N = time-period of 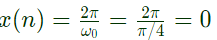
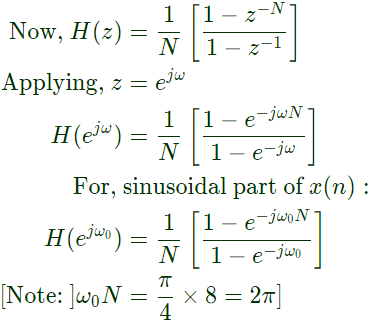
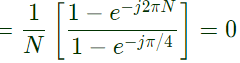 Therefore, for sinusoidal part of input, system output is zero. For dc part of input,
Therefore, for sinusoidal part of input, system output is zero. For dc part of input,
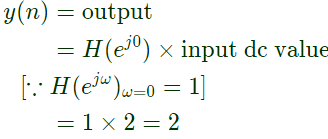 Thus, steady state output = 2.
Thus, steady state output = 2.
Q13: A discrete system is represented by the difference equation
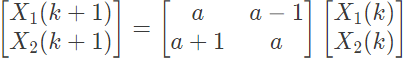 It has initial conditions X1(0) = 1; X2(0) = 0. The pole locations of the system for a = 1, are (SET-2 (2014))
It has initial conditions X1(0) = 1; X2(0) = 0. The pole locations of the system for a = 1, are (SET-2 (2014))
(a) 1 ± j0
(b) −1 ± j0
(c) ± 1 + j0
(d) 0 ± j1
Ans: (a)
Sol: Given that,
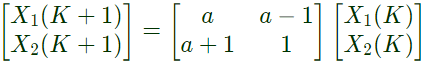 With initial conditions,
With initial conditions,
X1(0) = 1, X2(0) = 0
For a = 1, we can write,
 Applying z-transform on equation (i),
Applying z-transform on equation (i),
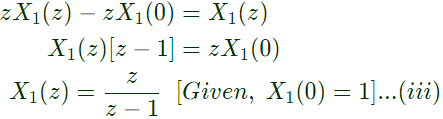 from equation (ii),
from equation (ii),
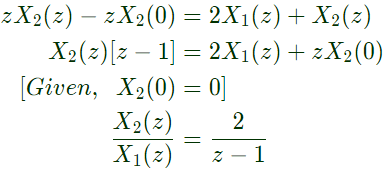 Thus, transfer function,
Thus, transfer function, 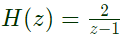
Therefore, pole location is z = 1.
Q14: Let 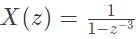 be the Z -transform of a causal signal x [n]. Then, the values of x[2] and x[3] are (SET-1 (2014))
be the Z -transform of a causal signal x [n]. Then, the values of x[2] and x[3] are (SET-1 (2014))
(a) 0 and 0
(b) 0 and 1
(c) 1 and 0
(d) 1 and 1
Ans: (b)
Sol: 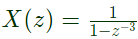 From z-transform defination,
From z-transform defination,
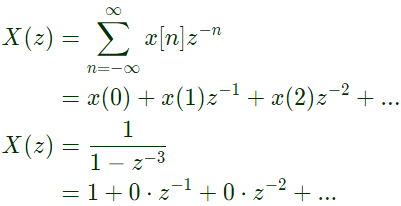 By comparision x(2) = 0 and x(3) = 1.
By comparision x(2) = 0 and x(3) = 1.
Q15: If x[n] = (1/3)∣n∣ − (1/2)nu[n], then the region of convergence (ROC) of its Z-transform in the Z-plane will be (2012)
(a) (1/3) < ∣z∣ < 3
(b) (1/3) < ∣z∣ < (1/2)
(c) (1/2) < ∣z∣ < 3
(d) (1/3) < ∣𝑧∣
Ans: (c)
Sol: 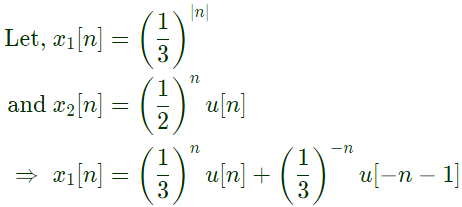
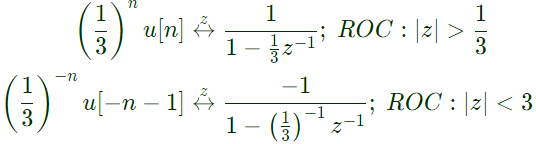
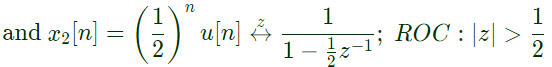
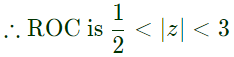
Q16: The z-transform of a signal x[n] is given by 4z−3 + 3z−1 + 2 − 6z2 + 2z3. It is applied to a system, with a transfer function H(z) = 3z−1 − 2. Let the output be y(n). Which of the following is true ? (2009)
(a) y(n) is non causal with finite support
(b) y(n) is causal with infinite support
(c) y(n) = 0; ∣n∣ > 3
(d) 
Ans: (a)
Sol: 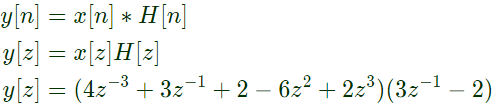
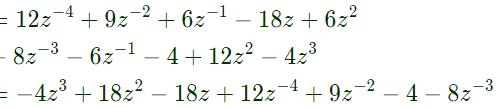
 Therefore, it is noncausal with finite support.
Therefore, it is noncausal with finite support.
Q17: Given  with ∣z∣ > a, the residue of X(z) zn − 1 at z = a for n ≥ 0 will be (2008)
with ∣z∣ > a, the residue of X(z) zn − 1 at z = a for n ≥ 0 will be (2008)
(a) an−1
(b) an
(c) nan
(d) nan−1
Ans: (d)
Sol: 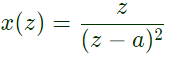
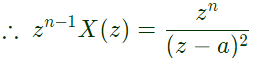 Since, z - a is a pole of second order, therefore residue at z = a
Since, z - a is a pole of second order, therefore residue at z = a
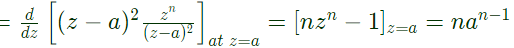
Q18: H(z) is a transfer function of a real system. When a signal x[n] = (1 + j)n is the input to such a system, the output is zero. Further, the Region of convergence (ROC) of (1 − (1/2)z −1)H(z) is the entire Z-plane (except z = 0). It can then be inferred that H(z) can have a minimum of (2008)
(a) one pole and one zero
(b) one pole and two zeros
(c) two poles and one zero
(d) two poles and two zeros
Ans: (d)
Q19: A signal is processed by a causal filter with transfer function G(s).
G(z) = αz−1 + βz−3 is a low pass digital filter with a phase characteristics same as that of the above question if (2007)
(a) α = β
(b) α = −β
(c) α = β(1/3)
(d) α = β(−1/3)
Ans: (a)
Sol: G(z) = αz−1 + βz−3
For, low frequency (z = 1) → G(1) = α+β...(i)
For, high frequency (z = −1) → G(−1) = −(α + β)...(ii)
For now, g(n) = {0, α, 0, β}
For linear phase FIR filter, g(n) should be either even symmetric or odd symmetric about virtual y-axis.
To, satisfy the above condition.
CASE: (i) α = −β
( odd symmetric about virtual y-axis)
But in this case,
G(1) = G(-1) = 0
i.e. at low frequency ⇒ G(z) = 0 and at high frequency ⇒ G(z) = 0
Thus in this case filter will be band-pass.
CASE: (ii) α = β
(even symmetric about virtual y-axis)
In this case,
At low frequency ⇒ G(z) = 2α and at high frequency ⇒ G(−1) = −2α
Filter will be either all pass or band-stop.
Now,
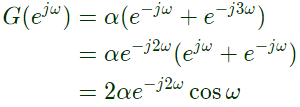
Q20: A signal is processed by a causal filter with transfer function G(s).
For a distortion free output signal wave form, G(s) must (2007)
(a) provides zero phase shift for all frequency
(b) provides constant phase shift for all frequency
(c) provides linear phase shift that is proportional to frequency
(d) provides a phase shift that is inversely proportional to frequency
Ans: (c)
Q21: X(z) = 1 − 3z−1, Y(z) = 1 + 2z−2 are Z transforms of two signals x[n], y[n] respectively. A linear time invariant system has the impulse response h[n] defined by these two signals as
h[n] = x[n - 1] * y[n]
where * denotes discrete time convolution. Then the output of the system for the input δ[n-1] (2007)
(a) has Z-transform z−1 X(z)Y(z)
(b) equals δ[n − 2] − 3δ[n − 3] + 2δ[n − 4] − 6δ[n − 5]
(c) has Z-transform 1 − 3z−1 + 2z−2 − 6z−3
(d) does not satisfy any of the above three
Ans: (b)
Sol: 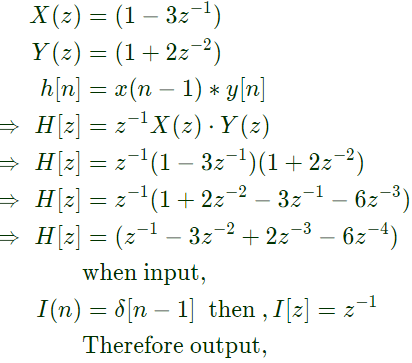
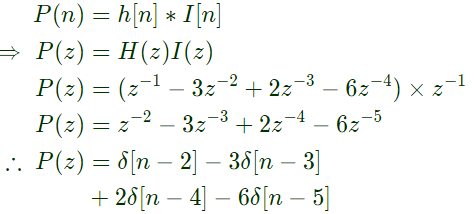
Q22: Consider the discrete-time system shown in the figure where the impulse response of G(z) is g(0) = 0, g(1) = g(2) = 1, g(3) = g(4) =...= 0
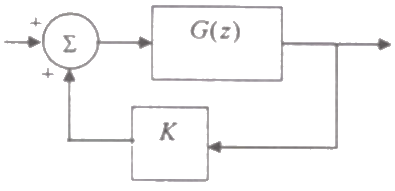 This system is stable for range of values of K (2007)
This system is stable for range of values of K (2007)
(a) [-1, 1/2]
(b) [-1, 1]
(c) [-1/2, 1]
(d) [-1/2, 2]
Ans: (a)
Sol: Given: g(1) = g(2) = 1
i.e. g[n] = δ[n−1] + δ[n−2]
Therefore,
G(z) = z−1 + z−2
Therefore overall transfer function of closed loop system,
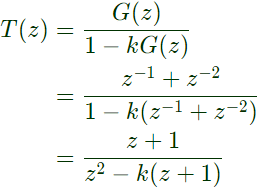 So the system will be stable if it's outer most pole will lie inside the unit circle.
So the system will be stable if it's outer most pole will lie inside the unit circle.
Location of poles,
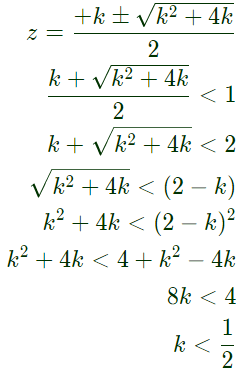
Q23: The discrete-time signal
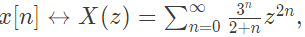 where ↔ denotes a transform-pair relationship, is orthogonal to the signal (2006)
where ↔ denotes a transform-pair relationship, is orthogonal to the signal (2006)
(a) 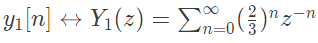
(b) 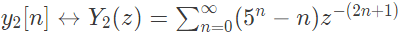
(c) 
(d) 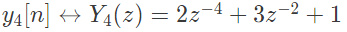
Ans: (b)
Sol: 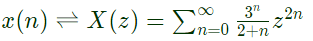 In X(z), power of z are even. Therefore, samples in x(n) are available at even instant of time.
In X(z), power of z are even. Therefore, samples in x(n) are available at even instant of time.
By observing all the options.
Option (B):
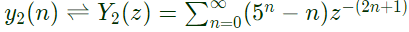 In y2(z), powers of z are odd. Therefore, samples in y2(n) are avialable only at odd instant of time.
In y2(z), powers of z are odd. Therefore, samples in y2(n) are avialable only at odd instant of time.
Hence, 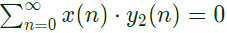 Thus, x(n) is orthogonal to y2(n).
Thus, x(n) is orthogonal to y2(n).
Q24: A discrete real all pass system has a pole at z = 2 ∠30°: it, therefore (2006)
(a) also has a pole at (1/2) ∠ 30°
(b) has a constant phase response over the z -plane: arg ∣H(z)∣ = constant
(c) has a constant phase response over the unit circle: arg |H(𝑒𝑖Ω)| = constant
(d) is stable only if it is anti-causal
Ans: (c)
Sol: For causal system, all the poles are inside the unit circle then system is stable, and converse in true for anti-causal system.

Q25: If u(t) is the unit step and δ(t) is the unit impulse function, the inverse z-transform of F(z) = 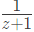 for k > 0 is (2005)
for k > 0 is (2005)
(a) (−1)k δ (k)
(b) δ(k) − (−1)k
(c) (−1)ku(k)
(d) u(k) − (−1)k
Ans: (b)
Sol: 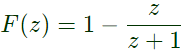
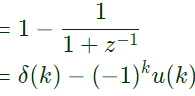
 Let
Let
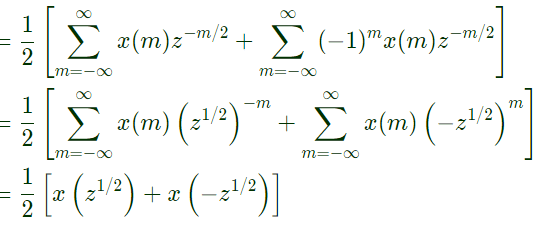
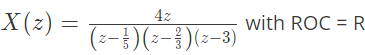 Which one of the following statements is true? (2023)
Which one of the following statements is true? (2023)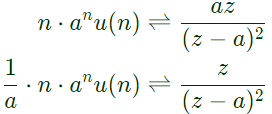
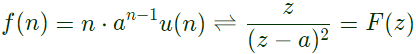 Time-shifting property,
Time-shifting property,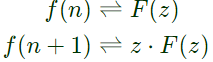
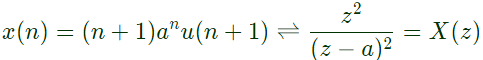 Thus,
Thus,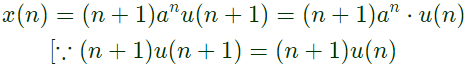
 Since, given pole zero is symmetrical about origin hence it is a all pass system.
Since, given pole zero is symmetrical about origin hence it is a all pass system.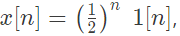 where 1[n] = 0 if n < 0, and 1[n] = 1 if n ≥ 0. The z-transform of x[n − k], k > 0 is
where 1[n] = 0 if n < 0, and 1[n] = 1 if n ≥ 0. The z-transform of x[n − k], k > 0 is 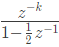 with region of convergence being (2020)
with region of convergence being (2020)
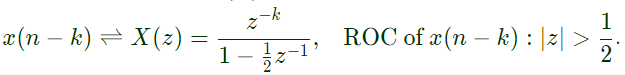
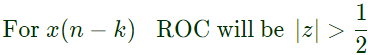
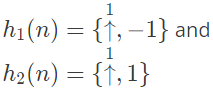 is shown in the figure below, where symbol ↑ denotes the time origin.
is shown in the figure below, where symbol ↑ denotes the time origin. The input sequence x(n) for which the cascade system produces an output sequence
The input sequence x(n) for which the cascade system produces an output sequence 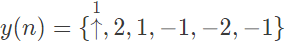 is (SET-2 (2017))
is (SET-2 (2017))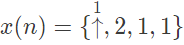
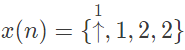
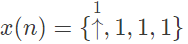
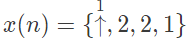
 Now,
Now,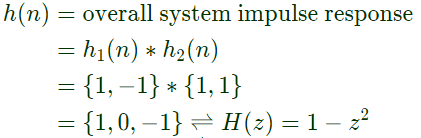
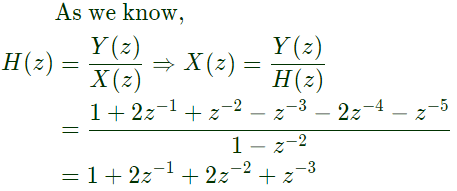
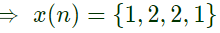
 (a) All three are high-pass filters.
(a) All three are high-pass filters.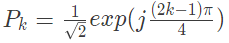 for k = 1, 2, 3, 4. The zeros of H(z) are all at z = 0. Let g[n] = jnh[n]. The value of g[8] equals ___________. (SET-1 (2017))
for k = 1, 2, 3, 4. The zeros of H(z) are all at z = 0. Let g[n] = jnh[n]. The value of g[8] equals ___________. (SET-1 (2017))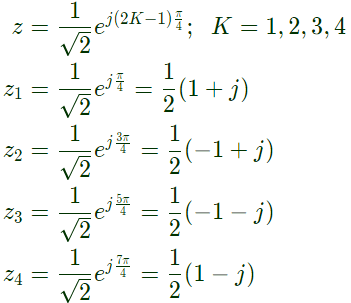 Now,
Now,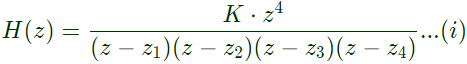 [As h(n) is causal and it starts from n=0, so numerator will have same order as denominator is having]. by solving equation (i)
[As h(n) is causal and it starts from n=0, so numerator will have same order as denominator is having]. by solving equation (i)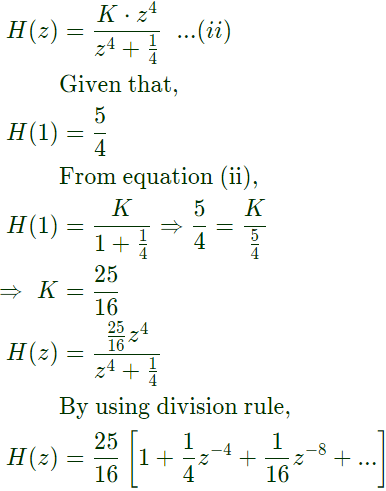
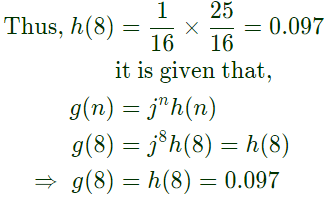
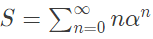 where ∣α∣ < 1. The value of α in the range 0 < α < 1, such that S = 2α is _______. (SET-1 (2016))
where ∣α∣ < 1. The value of α in the range 0 < α < 1, such that S = 2α is _______. (SET-1 (2016))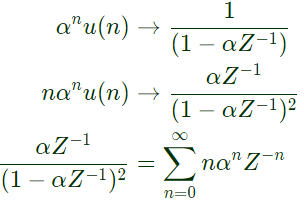 If we put Z = 1 in above equation, we get,
If we put Z = 1 in above equation, we get,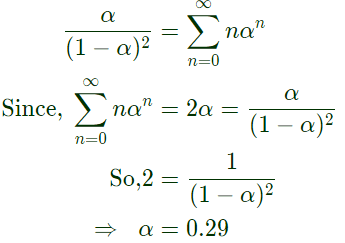
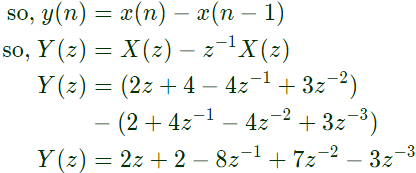
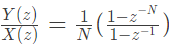 where, N represents the number of samples per cycle. The output y(n) of the system under steady state is (SET-2 (2014))
where, N represents the number of samples per cycle. The output y(n) of the system under steady state is (SET-2 (2014))
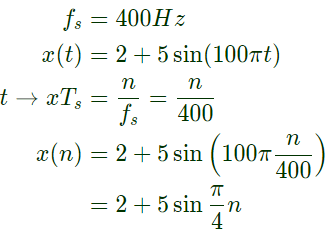
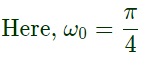 Therefore, N = time-period of
Therefore, N = time-period of 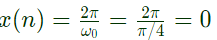
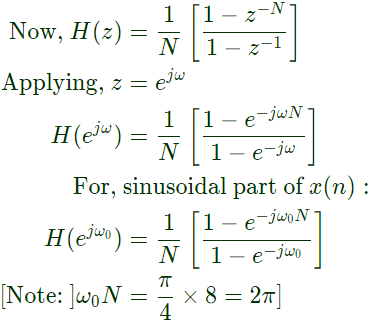
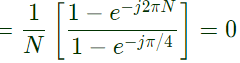 Therefore, for sinusoidal part of input, system output is zero. For dc part of input,
Therefore, for sinusoidal part of input, system output is zero. For dc part of input,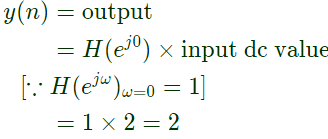 Thus, steady state output = 2.
Thus, steady state output = 2.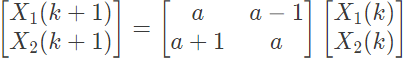 It has initial conditions X1(0) = 1; X2(0) = 0. The pole locations of the system for a = 1, are (SET-2 (2014))
It has initial conditions X1(0) = 1; X2(0) = 0. The pole locations of the system for a = 1, are (SET-2 (2014))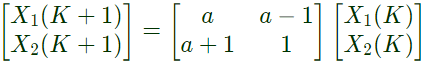 With initial conditions,
With initial conditions, Applying z-transform on equation (i),
Applying z-transform on equation (i),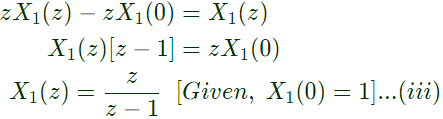 from equation (ii),
from equation (ii),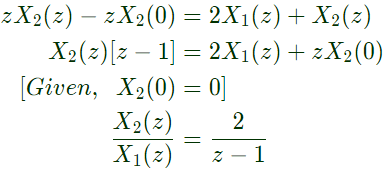 Thus, transfer function,
Thus, transfer function, 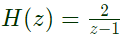
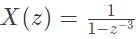 be the Z -transform of a causal signal x [n]. Then, the values of x[2] and x[3] are (SET-1 (2014))
be the Z -transform of a causal signal x [n]. Then, the values of x[2] and x[3] are (SET-1 (2014))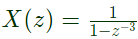 From z-transform defination,
From z-transform defination,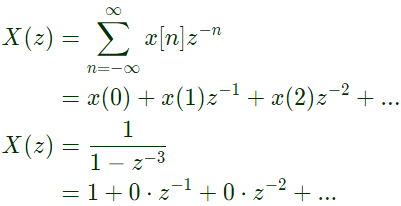 By comparision x(2) = 0 and x(3) = 1.
By comparision x(2) = 0 and x(3) = 1.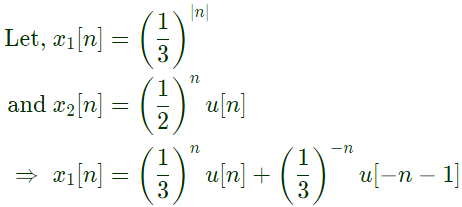
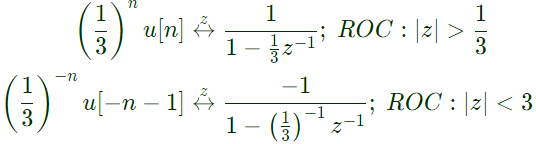
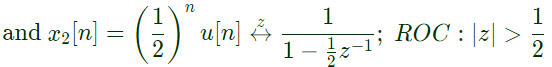
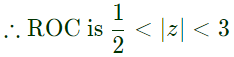
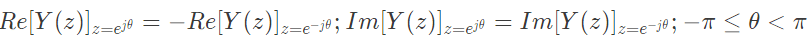
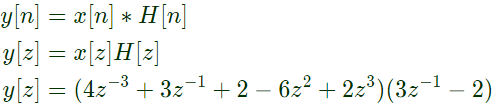
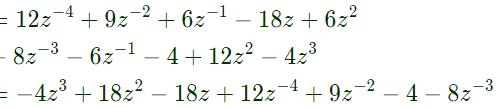
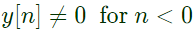 Therefore, it is noncausal with finite support.
Therefore, it is noncausal with finite support. with ∣z∣ > a, the residue of X(z) zn − 1 at z = a for n ≥ 0 will be (2008)
with ∣z∣ > a, the residue of X(z) zn − 1 at z = a for n ≥ 0 will be (2008)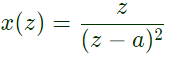
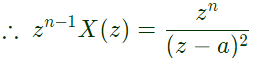 Since, z - a is a pole of second order, therefore residue at z = a
Since, z - a is a pole of second order, therefore residue at z = a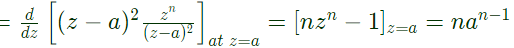
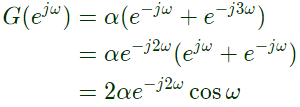
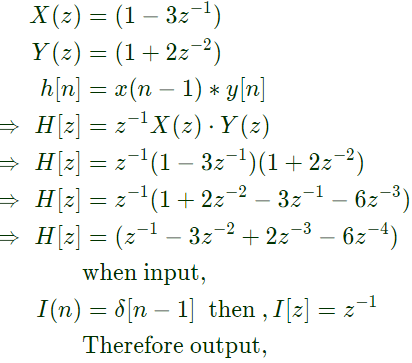
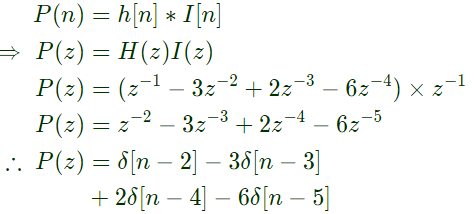
 This system is stable for range of values of K (2007)
This system is stable for range of values of K (2007)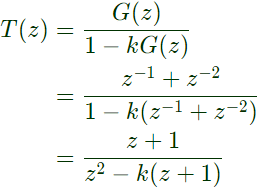 So the system will be stable if it's outer most pole will lie inside the unit circle.
So the system will be stable if it's outer most pole will lie inside the unit circle.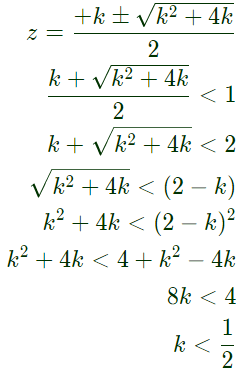
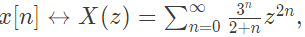 where ↔ denotes a transform-pair relationship, is orthogonal to the signal (2006)
where ↔ denotes a transform-pair relationship, is orthogonal to the signal (2006)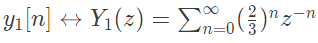
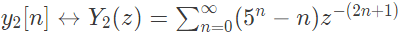

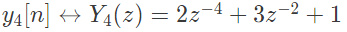
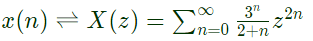 In X(z), power of z are even. Therefore, samples in x(n) are available at even instant of time.
In X(z), power of z are even. Therefore, samples in x(n) are available at even instant of time.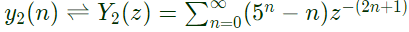 In y2(z), powers of z are odd. Therefore, samples in y2(n) are avialable only at odd instant of time.
In y2(z), powers of z are odd. Therefore, samples in y2(n) are avialable only at odd instant of time.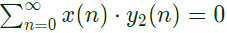 Thus, x(n) is orthogonal to y2(n).
Thus, x(n) is orthogonal to y2(n). 
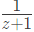 for k > 0 is (2005)
for k > 0 is (2005)