Previous Year Questions: Recurrence Relation | Algorithms - Computer Science Engineering (CSE) PDF Download
Q1: Let T(n) be the recurrence relation defined as follows:
T(0) =1
T(1) = 2, and
T(n) = 5T (n - 1) - 6T(n - 2) for n ≥ 2
Which one of the following statements is TRUE? (2024 SET-2)
(a) T(n) = Θ (2n)
(b) T(n) = Θ (n2n)
(c) T(n) = Θ (3n)
(d) T(n) = Θ (n3n)
Ans: (a)
Sol:
Given
T0 = 1; T1 =2; Tn = 5Tn-1 - 6Tn-2 for (n ≥ 2)
Observations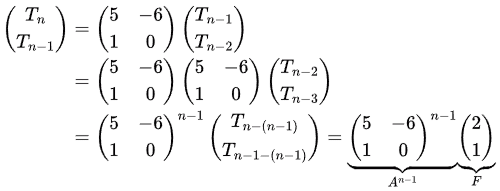
A is invertible 2 × 2 matrix. Hence, we can use the power of diagonalization to solve for An−1 neatly.
Diagonalization
∧ = P-1 AP or A = P∧ P-1 where ∧ is 2 x 2 diagonal matrix and ∧i,i = λi, here λi is eigen value of A. P is 2 x 2 invertible matrix such that P = (e1 e2) where ei is eigenvector corresponding to λi. Hence, using diagonalization we can represent any matrix in terms of its eigenvalues and eigenvectors.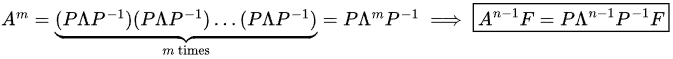
Eigen values of A are 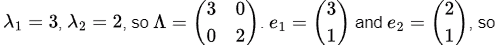
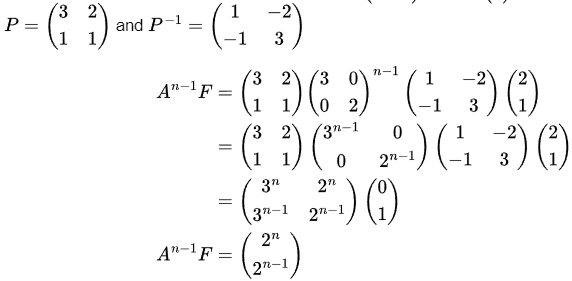
Final Equation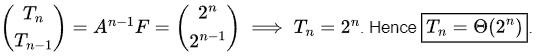
Q2: Consider the following recurrence relation: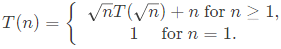
Which one of the following options is CORRECT? (2024 SET-1)
(a) T(n) = Θ(n log log n)
(b) T(n) = Θ(n log n)
(c) T(n) = Θ(n2 log n)
(d) T(n) = Θ(n2 log log n)
Ans: (a)
Sol: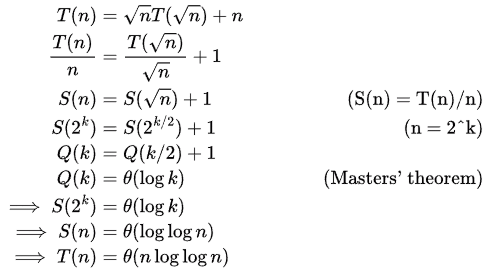
Option (A) is correct
Clarification over Solution to Q(K)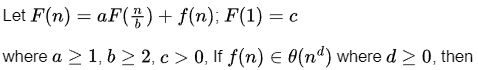
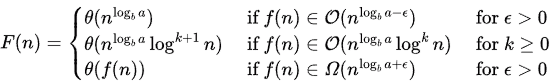

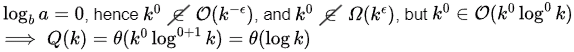
Q3: For constants a ≥ 1 and b >1, consider the following recurrence defined on the non-negative integers: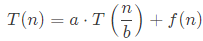
Which one of the following options is correct about the recurrence T(n)? (2021 SET-2)
(a) if f(n) is n log2(n), then T(n) is Θ (n log2(n)).
(b)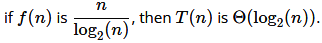
(c)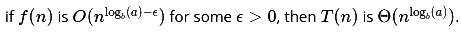
(d)
Ans: (c)
Sol: Options A and B are definitely wrong, condition on f(n) can’t be independent of a and b in any case, it should take both a and b into account.
Option C is correct. standard case of master theorem, if f(n) is polynomial time smaller than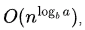
Then 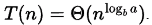 (see case 1 below).
(see case 1 below).
Theorem 4.1 (Master theorem)
Let a ≥ 1 and b > 1 be constants, let f(n) be a function, and let t(n) be defined on the nonnegative integers by the recurrence
T(n) = aT(n/b) + f(n),
where we interpret n/b to mean either [n/b] or [n/b]. Then T(n) has the following asymptotic bounds:
If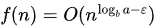 for some constant ε > 0, Then
for some constant ε > 0, Then 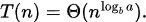
If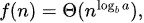 Then
Then 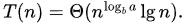
If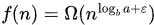 for some constant ε > 0, and if af(n/b) ≤ cf(n) for some constant c < 1 and all sufficiently large n,
for some constant ε > 0, and if af(n/b) ≤ cf(n) for some constant c < 1 and all sufficiently large n,
then T(n) = Θ(f(n)).
Q4: Consider the following recurrence relation.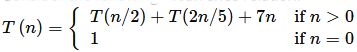
Which one of the following options is correct? (2021 SET-1)
(a) T(n) = Θ(n5/2)
(b) T(n) = Θ(n log n)
(c) T(n) = Θ(n)
(d) T(n) = Θ((log n)5/2)
Ans: (c)
Sol: At first, draw two levels of the recursion tree: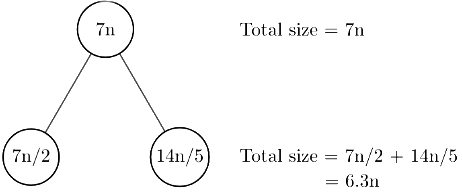
Size of the problem will reduce as we go down a level each time in the tree.
Hence, in this case root will be the dominant part.
Final ans is T(n) = Θ(n) (order of the root) (you have to ans in less than 30 sec!)
Let 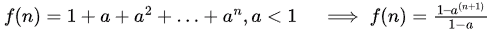
When 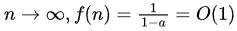 since
since 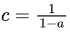 is a constant.
is a constant.
We can see that the size of problem reduces geometrically, and root is the dominating part.
Note: Apply the following method for divide and conquer recursions because the size of the problem reduces geometrically. Not for subtract and conquer where it might reduce arithmetically!
And to apply this idea, all the conditions of Master theorem must be satisfied.
Everything given below is not required for GATE, it's just to explain the idea.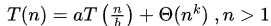
T(1) = c
(Assume all conditions of the Master theorem to be true here, b > 1).
Let height of this tree be h,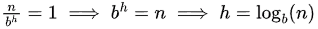
No. of leaves 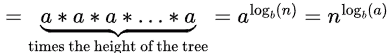
Here’s the relation with master theorem:
Case 1 (root is dominant): 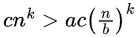
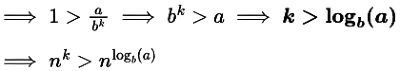
This case of Master theorem says T(n) = Θ (nk), which is nothing but the order of root.
(We are kind a deriving cases of the master theorem using intuition)
Case 2 (root is equal to all levels): 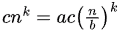
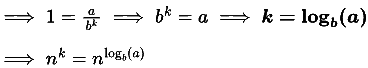
According to the Master theorem, T(n) = Θ(nk log(n)).
All the levels are equally dominant, hence final result will be the sum of all levels.
That is, size of a particular level × the height ⇒ nk x logb(n), Hence T(n) = Θ (nk logb(n)).
Case 3 (leaf level is dominant): 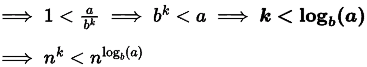
As the leaves’ levels are dominant, Ans will be in the order of the leaf’s level = Order of no of leaves in the tree (because base condition will be a constant)
Hence 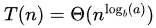
Q5: The master theorem (2020)
(a) assumes the subproblems are unequal sizes
(b) can be used if the subproblems are of equal size
(c) cannot be used for divide and conquer algorithms
(d) cannot be used for asymptotic complexity analysis
Ans: (b)
Sol: It divides the subproblem into each of size n/b.
Q6: For parameters a and b, both of which are ω(1),T(n) = T(n1/a)+1, and T(b) = 1. Then T(n) is (2020)
(a) Θ(loga logb n)
(b) Θ(logab n)
(c) Θ(logb loga n)
(d) Θ(log2 log2 n)
Ans: (a)
Sol: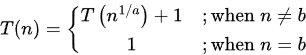
Now, 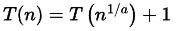
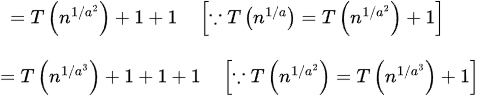
After k iterations, 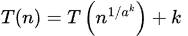
When 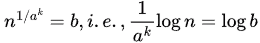
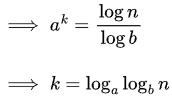
[∵ a&b are ω(1), so a&b are some function of n and not constant. So a&b can’t be replaced with 2]
So, option D is rejected.
Now, 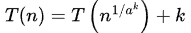
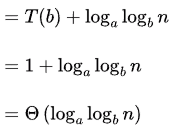
So, the correct answer is A.
Q7: The running time of an algorithm is given by: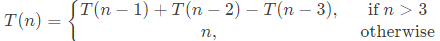
Then what should be the relation between T(1), T(2), T(3), so that the order of the algorithm is constant? (2018)
(a) T(1) = T(2) = T(3)
(b) T(1) + T(3) = 2T(2)
(c) T(1) - T(3) = T(2)
(d) T(1) + T(2) = T(3)
Ans: (a)
Sol: For sufficiently large n,
T(n) = Tn - 1) + T(n - 2) - T(n - 3)
If the order of the algorithm for which above recurrence is applicable for the time complexity, is a constant,
T(n) =T(n-1).
⇒ T(n) = T(n) + T(n - 2) - T(n - 3)
⇒ T(n - 2 = T(n - 3)
Going like this, we must have T(1) = (T(2) = T(3).
Q8: The recurrence relation that arises in relation with the complexity of binary search is: (2017)
(a) T(n) = 2T (n/2) + k, k is a constant
(b) T(n) = T (n/2) + k, k is a constant
(c) T(n) = T (n/2) + log n
(d) T(n) = T (n/2) + n
Ans: (b)
Sol: Searching for only one half of the list. leading to T(n/2) + constant time in comparing and finding mid element.
Q9: Consider the recurrence function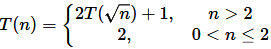
Then T(n) in terms of θ notation is (2017 SET-2)
(a) θ(loglogn)
(b) θ(logn)
(c) θ(√n)
(d) θ(n)
Ans: (b)
Sol: T(n) = 2T(√n) + 1
Put, n =2m which implies √n = n1/2 = 2m/2
⇒ T(2m) = 2T(2m/2) + 1
Put, T(2m) = S(m) which implies T(2m/2) = S(m/2)
⇒ S(m) = 2S(m/2) + 1
Using case 1 of master method ,
= Θ(m) = Θ (log n)
Q10: Consider the following recurrence:
T(n) = 2T(√n) + 1, T(1) = 1
Which one of the following is true? (2016)
(a) T(n) = Θ(log log n)
(b) T(n) = Θ(log n)
(c) T(n) = Θ(√n)
(d) T(n) = Θ(n)
Ans: (b)
Sol: 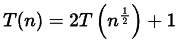
Q11: Suppose you want to move from 0 to 100 on the number line. In each step, you either move right by a unit distance or you take a shortcut. A shortcut is simply a pre-specified pair of integers i,j with i<j. Given a shortcut i, j if you are at position i on the number line, you may directly move to j. Suppose T(k) denotes the smallest number of steps needed to move from k to 100. suppose further that there is at most 1 shortcut involving any number, and in particular from 9 there is a shortcut to 15. Let y and z be such that T(9) = 1 + min(T(y), T(z)). Then the value of the product yz is_______. (2014 SET-3)
(a) 100
(b) 150
(c) 50
(d) 200
Ans: (b)
Sol: T(k) is the smallest number of steps needed to move from k to 100.
Now, it is given that y and z are two numbers such that,
T(9) = 1 + min(T(y), T(z)), i.e.,
T(9) = 1 + min (Steps from y to 100 , Steps from z to 100), where y and z are two possible values that can be reached from 9.
One number that can be reached from 9 is 10, which is the number obtained if we simply move one position right on the number line. Another number is 15, the shortcut path from 9, as given in the question. So, we have two paths from 9, one is 10 and the other is 15.
Therefore, the value of y and z is 10 and 15 (either variable may take either of the values).
Thus, yz = 150.
Q12: Which one of the following correctly determines the solution of the recurrence relation with T(1) = 1? (2014 SET-2)
T(n) = 2T(n/2) + logn
(a) θ(n)
(b) θ(nlogn)
(c) θ(n2)
(d) θ(logn)
Ans: (a)
Sol: f(n) = log n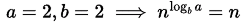
So, f(n) = log n = O (n1- ϵ) we can take any ϵ from 0-1 for example 0.5 which gives log n = O(√(n)),
So, Master theorem Case 1, and answer will be 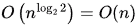
Alternate way:
T(1) = 1T(2) = 2T(1) + log2 = 3 = 3n - 2T(4)
= 2T(2) + log 4 = 8= 3n - 4T(8)
= 2T(4) + log 8 = 19 = 3n - 5T(16
= 2T(8) + log 16 = 42 = 3n - 6
The second term being subtracted is growing at a lower rate than the first term. So, we can say T(n) = O(n).
Q13: The recurrence relation capturing the optimal execution time of the Towers of Hanoi problem with n discs is (2012)
(a) T(n) = 2T(n - 2) + 2
(b) T(n) = 2T(n - 1) + n
(c) T(n) = 2T(n/2) + 1
(d) T(n) = 2T(n - 1) + 1
Ans: (d)
Sol: Recurrence relation for Towers of Hanoi is
T(1) = 1
T(n) = 2T(n - 1) + 1
So Answer should be (D)
Q14: Let T(n) be defined by T(1) = 10 and T(n + 1) = 2n + T(n) for all integers n ≥ 1.
Which of the following represents the order of growth of T(n) as a function of n? (2011)
(a) O(n)
(b) O(n log n)
(c) O(n2)
(d) O(n3)
Ans: (c)
Sol: T(n + 1) = 2n + T(n)
= 2n + 2(n - 1) + T(n - 1)
= 2n + 2(n - 1) + 2(n - 2) + T(n - 2).....
= 2n + 2(n - 1) + 2(n - 2)... 2(1) + T(1)
= 2(n + n - 1 + n - 2.....1) + T(1)
= 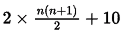
= O(n2)
Q15: The running time of an algorithm is represented by the following recurrence relation: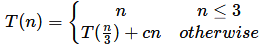
Which one of the following represents the time complexity of the algorithm? (2009)
(a) θ(n)
(b) θ(n log n)
(c) θ(n2)
(d) θ(n2logn)
Ans: (a)
Sol: Comparing with the recurrence form of Master Theorem
T(n) = aT(n/b) + f(n)
a = 1, b = 3, logb a = 0
So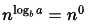
f(n) = cn
So, 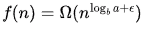 holds for any ϵ < 1 and this is the third case of Master theorem. But Master theorem also requires (only case 3) that regularity condition be satisfied (this ensures that f(n) is still dominant when the recurrence go deeper) which is af(n/b) ≤ df(n) for some d < 1 and all sufficiently large n.(Using d here as c is already used in f(n))
holds for any ϵ < 1 and this is the third case of Master theorem. But Master theorem also requires (only case 3) that regularity condition be satisfied (this ensures that f(n) is still dominant when the recurrence go deeper) which is af(n/b) ≤ df(n) for some d < 1 and all sufficiently large n.(Using d here as c is already used in f(n))
Here we get, f(n/3) ≤ df(n)
⇒ cn/3 ≤ dcn ⇒ 1/3 ≤ d
Thus we can use any 1/3 ≤ d < 1 to satisfy the regularity condition and Master theorem case 3 is satisfied. Now, applying case 3 we get
T(n) = Θ(f(n)) = Θ(n)
Q16: When n =2k for some k ≥ 0, the recurrence relation T(n) = √(2)T(n/2) + √n, T(1) = 1 evaluates to : (2008)
(a) √(n) (log n+1)
(b) √(n) log n
(c) √(n) log √(n)
(d) n log √n
Ans: (a)
Sol: T(n) = √(2) T (n/2) + √n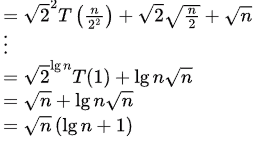
If we use Master theorem we get option B. But one must know that Master theorem is used to find the asymptotic bound and not an EXACT value. And in the question here it explicitly says "evaluates to".
Q17: Let xn denote the number of binary strings of length n that contain no consecutive 0s. (2008)
The value of x5 is
(a) 5
(b) 7
(c) 13
(d) 16
Ans: (c)
Sol:
Step 1: Understanding the recurrence relation
A binary string of length n can end in either:
1 → The remaining n−1 digits can be any valid binary string of length n−1.
0 → The previous digit must be 1 to avoid consecutive 0s. The remaining n−2 digits can be any valid binary string of length n−2.
Thus, the recurrence relation is:
xn = xn−1+xn−2
which follows the Fibonacci sequence but with different base values.
Step 2: Base Case
- x1=2 → Strings: {"0", "1"}
- x2=3 → Strings: {"00" (not allowed), "01", "10", "11"} → Valid: {"01", "10", "11"}
Step 3: Compute x5
Using the recurrence relation:
5 = x4 + x3 = 8 + 5 =13
Q18: Let xn denote the number of binary strings of length n that contain no consecutive 0s.
Which of the following recurrences does xn satisfy? (2008)
(a) xn = 2xn-1
(b) xn = x[n/2] + 1
(c) xn = x[n/2] + n
(d) xn = Xn-1 + xn-2
Ans: (d)
Sol:
01 - 2
01 10 11 - 3
010 011 101 110 111 - 5
0101 0110 0111 1010 1011 1101 1110 1111- 8
SO, xn = xn-1 + xn-2 (For all the strings ending in 1, we get two new strings ending in either 0 or 1 and for all strings ending in 0, we get a new string ending in 1. So, the new set of strings for xn, will have exactly xn-1 strings ending in 1 and xn-2 strings ending in 0)
x5 = 8 + 5 =13.
Q19: Consider the following recurrence:
T(n)=2T([√n]) + 1, T(1) = 1
Which one of the following is true? (2006)
(a) T(n)=Θ(loglogn)
(b) T(n)=Θ(logn)
(c) T(n)=Θ(√n)
(d) T(n)=Θ(n)
Ans: (b)
Sol:
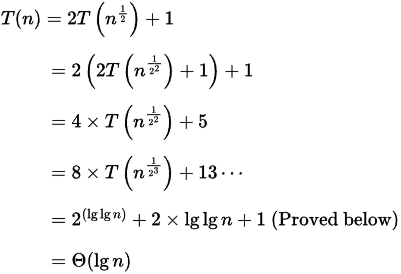
Q20: Let T(n) be a function defined by the recurrence
T(n) = 2T(n/2) + √n for n ≥ 2 and
T(1) = 1
Which of the following statements is TRUE? (2005)
(a) T(n) = Θ(log n)
(b) T(n) = Θ(√n)
(c) T(n) = Θ(n)
(d) T(n) = Θ(n log n)
Ans: (c)
Sol: Option C is the answer. It can be done by Master's theorem.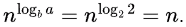
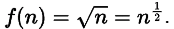
So, 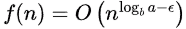 is true for any real ϵ, 0 < ϵ < 1/2.
is true for any real ϵ, 0 < ϵ < 1/2.
Hence Master theorem Case 1 satisfied,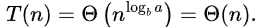
Q21: Suppose T(n) = 2T(n/2) + n, T(0) = T(1) = 1
Which one of the following is FALSE? (2005)
(a) T(n) = O(n2)
(b) T(n) = Θ(n log n)
(c) T(n) = Ω(π2)
(d) T(n) = O(n log n)
Ans: (c)
Sol: Applying Masters theorem,
T(n) = Θ(n log n)
So, it cannot be Ω(n2).
Hence, answer is (C).
Q22: Consider a list of recursive algorithms and a list of recurrence relations as shown below. Each recurrence relation corresponds to exactly one algorithm and is used to derive the time complexity of the algorithm.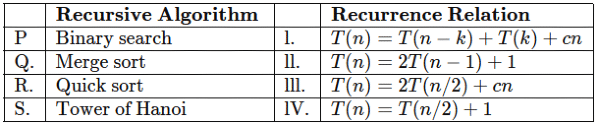
Which of the following is the correct match between the algorithms and their recurrence relations? (2004)
(a) P-II, Q-III, R-IV, S-I
(b) P-IV, Q-III, R-I, S-II
(c) P-III, Q-II, R-IV, S-I
(d) P-IV, Q-II, R-I, S-III
Ans: (b)
Sol: For binary search on n elements we pick a path of n/2 elements after doing a single comparison (0(1)) and discard the remaining n/2 elements So, T(n) = T(n/2) + 1.
For merge sort on n elements we divide the array into two equal parts containing n/2 elements, recursively merge sort them and finally merges the 2 arrays in O(n) time. So,
T(n) = 2T(n/2) + сn.
For quick sort on n elements we split the array based on the position of the pivot. If pivot happens to be the k + 1th element in the sorted array, we do a recursive call using k elements and n - k - 1 elements and we need O(n) time to decide the position of the pivot.
So, T(n) = T(n - k - 1) + T(k) + cn. (A -1 is missing in the question option).
For Tower of Hanoi using n disks, to position the first disk we have to replace n 1 disks two times. To place the remaining disks we have to recursively solve the problem thus giving T(n) = 2T(n - 1) + 1.
Q23: The recurrence equation (2004)
T(1) = 1
T(n) = 2T(n - 1) + n, n ≥ 2
evaluates to
(a) 2n+1 - n - 2
(b) 2n- n
(c) 2n+1 - 2n - 2
(d) 2n + n
Ans: (a)
Sol: 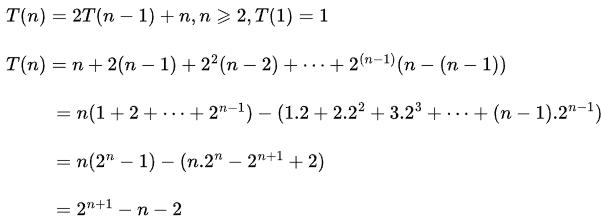
Q24: Consider the following recurrence relation (2003)
T(1)=1
T(n+1)=T(n)+ [√n + 1] for all n ≥ 1
The value of T(m2) for m ≥ 1 is
(a) (m/6) (21m - 39) + 4
(b) (m/6) (4m2 - 3m + 5)
(c) (m/2) (m2.5 - 11m + 20) - 5
(d) (m/6) (5m3- 34m2 + 137m - 104) + (5/6)
Ans: (b)
Sol:
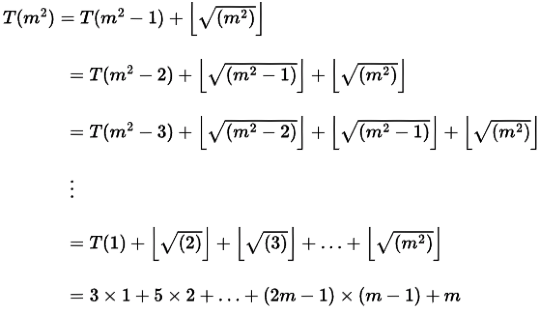
(We are taking floor of square root of numbers, and between successive square roots number of numbers are in the series 3, 5, 7... like 3 numbers from 1..4, 5 numbers from 5 - 9 and so on).
We can try out options here or solve as shown at end:
Put m = 5, T(25) = 3 x 1 + 5 × 2 + 7 × 3 + 9 × 4 + 5 = 75
A. 59
B. 75
C. non-integer
D. 297.5
So, answer must be B.
Q25: The running time of the following algorithm
Procedure A(n)
If n ≤ 2 return (1) else return (A(√n)); (2002)
is best discribed by
(a) O(n)
(b) O(log n)
(c) O(loglogn)
(d) 0(1)
Ans: (c)
Sol: The complexity will be the number of times the recursion happens which is equal to the number of times we can take square root of n recursively, till n becomes 2.
T(n) = T([√n]) + 1
T(2) = 1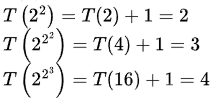
So, T(n) = lg lg n + 1 = O(log log n)
Q26: The solution to the recurrence equation T(2k) = 3T (2k-1) + 1, T(1) = 1 is (2002)
(a) 2k
(b)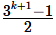
(c)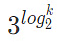
(d)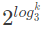
Ans: (b)
Sol: Let x = 2
T(x) = 3T(x/2) + 1
We can apply Master's theorem case 1 with a = 3 and b = 2 as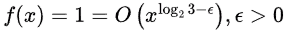
So,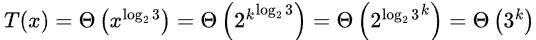
So, only option possible is B.
We can also directly solve as follows:
T(x) = 3T(x/2)+1
= 9T (x/4) + 1 + 3
: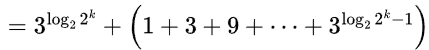
(recursion depth is log2 x and x = 2k)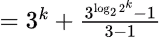
(Sum to n terms of GP with a = 1 and r = 3)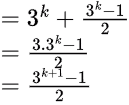
OR
T (2k) = 3T (2k-1) +1
= 32T (2k-2) + 1 + 3
:
= 3kT (2k-k) + (1 + 3 + 9 + ... + 3 - 1)
(recursion depth is k)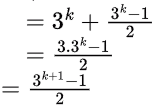
Q27: The recurrence relation (1996)
T(1) = 2
T(n) = 3T(n/4) + n
has the solution T(n) equal to
(a) O(n)
(b) O(log n)
(c) O(n3/4)
(d) None of the above
Ans: (a)
Sol: According to Master theorem,
T(n) = aT(n/b) + f(n) can be expressed as: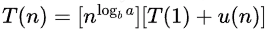
Where u(n) = 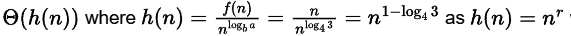
where r = 0.
So, 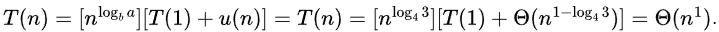
Q28: The recurrence relation that arises in relation with the complexity of binary search is: (1994)
(a) T(n) = 2T (n/2) + k, k is a constant
(b) T(n) = T (n/2) + k, k is a constant
(c) T(n) = T (n/2) + log n
(d) T(n) = T (n/2) + n
Ans: (b)
Sol: Searching for only one half of the list. leading to T(n/2) + constant time in comparing and finding mid element.
|
81 videos|113 docs|33 tests
|
FAQs on Previous Year Questions: Recurrence Relation - Algorithms - Computer Science Engineering (CSE)
| 1. What is a recurrence relation in mathematics? |  |
| 2. How do you solve a linear recurrence relation? |  |
| 3. What are some common types of recurrence relations? |  |
| 4. What is the significance of initial conditions in recurrence relations? |  |
| 5. Can recurrence relations be applied in computer science? |  |
















