Worksheet Solution: Patterns in Mathematics | Worksheets with Solutions for Class 6 PDF Download
| Table of contents |

|
| Learning Pattern |

|
| Fill in the Blanks |

|
| True or False |

|
| Word Problem |

|
Learning Pattern
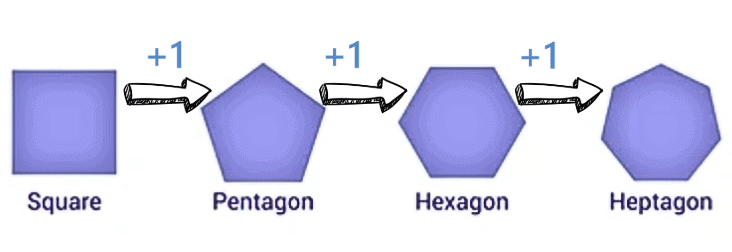
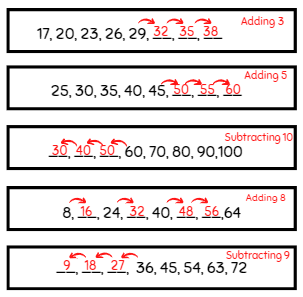
Q1: Find out the missing numbers and figure out what the pattern rule is for each box.
Q2: Find out what type of pattern is represented by the given diagram and write number pattern for the same 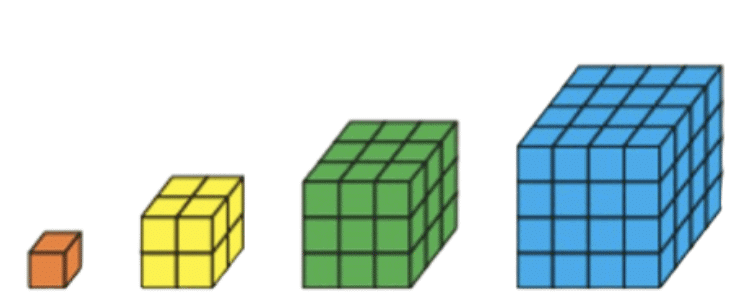
Ans: The represented pattern is cube numbers
Number pattern is 1, 8, 27, 64, ... and so on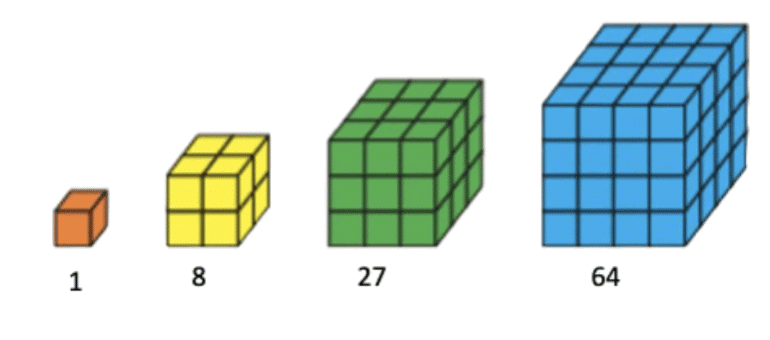 Q3: Find out what type of pattern is represented by the given diagram and write number pattern for the same
Q3: Find out what type of pattern is represented by the given diagram and write number pattern for the same

Ans: The represented pattern is of odd numbers
Number pattern is 1, 3, 5, 7, 9, 11 ... and so on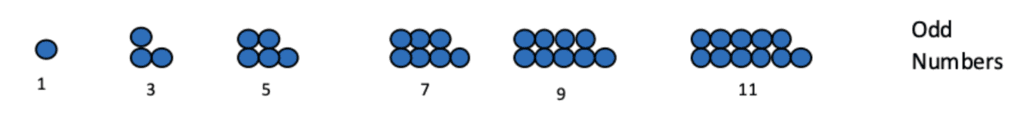
Fill in the Blanks
Q1: A ________ polygon is a shape with all sides and angles equal.
Ans: regular
The term "regular" in geometry means that all sides and angles of the polygon are equal.
Q2: The sequence 1, 8, 27, 64, ... represents the ________ of numbers.
Ans: cubes
These numbers are the cubes of the natural numbers: , .........
Q3: ________ numbers can be represented as dots forming a perfect square.
Ans: Square
Square numbers can be visualized by arranging dots in a grid where the number of rows equals the number of columns.
Q4: The pattern 2, 4, 6, 8, 10, ... is a sequence of ________ numbers.
Ans: even
This sequence is formed by adding 2 to the previous number, which creates a sequence of even numbers.
Q5: ________ numbers increase by the same amount each time, and this sequence is called counting numbers.
Ans: Natural
The natural or counting numbers increase by 1 each time: 1, 2, 3, 4, ...
True or False
Q1: The sequence 1, 4, 9, 16, 25, ... is an example of cube numbers.
Ans: False
This sequence is an example of square numbers, not cube numbers.
Q2: A regular pentagon has equal sides but different angles.
Ans: False
A regular pentagon has both equal sides and equal angles.
Q3: The sequence of odd numbers starts with 1, 3, 5, 7, ...
Ans: True
The odd number sequence starts with 1 and increases by 2 each time.
Q4: A shape sequence starting with a square and adding one side each time would form polygons with increasing numbers of sides.
Ans: True
This sequence would start with a square (4 sides), then a pentagon (5 sides), and so on, each with one more side.
Q5: The number 36 can be both a square number and a triangular number.
Ans: True
The number 36 is unique in that it can be represented both as a square number (6x6) and as a triangular number.
Word Problem
Q1: Riya is stacking books in a pyramid shape. The first row has 1 book, the second has 3, the third has 6. If she continues this pattern, how many books will be in the fifth row?
Ans: The books in each row follow a pattern:
- 1st row: 1
- 2nd row: 1 + 2 = 3
- 3rd row: 1 + 2 + 3 = 6
- 4th row: 1 + 2 + 3 + 4 = 10
- 5th row: 1 + 2 + 3 + 4 + 5 = 15
The fifth row will have 15 books.
Q2: A honeycomb follows a hexagonal pattern. If the first row has 1 cell, the second has 7 cells, and the third has 19 cells, how many will be in the fourth row?
Ans: The number of cells follows this pattern:
- 1st row = 1
- 2nd row = 1 + 6 = 7
- 3rd row = 7 + 12 = 19
- 4th row = 19 + 18 = 37
The fourth row will have 37 cells.
Q3: A school’s staircase follows a pattern: The first step has 2 tiles, the second has 4, the third has 6. How many tiles will be on the 10th step?
Ans: Each step increases by 2 tiles. The sequence follows:
- 1st step = 2
- 2nd step = 4
- 3rd step = 6
- 4th step = 8
- …
- 10th step = 2 × 10 = 20
The 10th step will have 20 tiles.
Q4: Give a diagrammatic representation of triangular numbers.
Ans: A triangular number is the total number of dots that can be arranged in an equilateral triangle.
For example: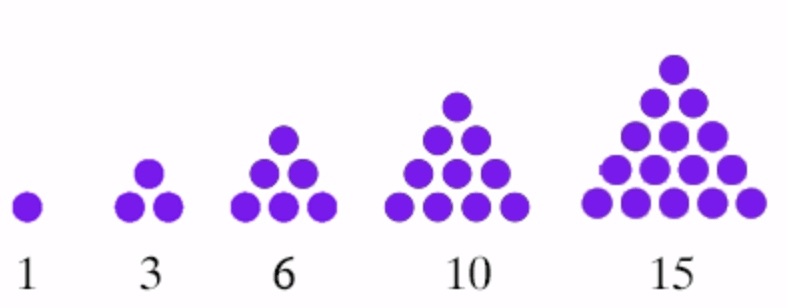
Q5: Represent 36 as both triangular and square numbers.
Ans: (i) 36 as a triangular number

(ii) 36 as a square number

FAQs on Worksheet Solution: Patterns in Mathematics - Worksheets with Solutions for Class 6
| 1. What are patterns in mathematics? |  |
| 2. Why are learning patterns important in math education? |  |
| 3. How can I identify a pattern in a sequence of numbers? |  |
| 4. What are some common types of mathematical patterns? |  |
| 5. How can I practice finding patterns in mathematics? |  |