Rank Correlation Test | Crash Course for UGC NET Commerce PDF Download
| Table of contents |

|
| Spearman Rank Correlation Test-Explanation |

|
| Spearman Rank Correlation Test for Heteroskedasticity |

|
| Spearman Rank Order Correlation Test |

|
| Monotonic Relationship |

|
Spearman Rank Correlation Test-Explanation
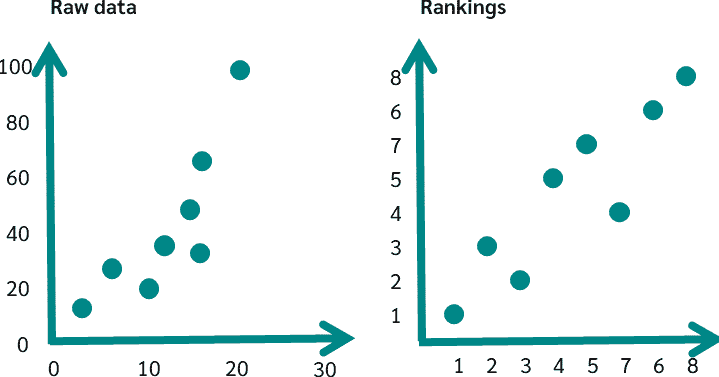
The Spearman Rank Correlation Test is a nonparametric statistic used to assess how well a monotonic relationship exists between two variables. Unlike the Pearson Correlation, which relies on the actual data values, the Spearman test first ranks the data points for both variables from smallest to largest. These ranks are then used in the correlation analysis instead of the raw data values.
This method makes the Spearman test more robust to outliers and assumptions about data distribution, such as normality. It can detect monotonic relationships (where one variable consistently increases or decreases with the other) but not nonlinear relationships.
Here are the main steps to perform the Spearman Rank Correlation Test:
- Rank the Data: Assign a rank to each data value for both variables, from 1 to n, where n is the total number of data points. For tied values, assign the average rank.
- Calculate Rank Differences: Compute the difference between the ranks of each paired data point (one from each variable).
- Square the Differences: Square each of these differences.
- Sum the Squared Differences: Add up all the squared differences.
- Compute the Correlation Coefficient (ρ): Use the sum of squared differences and the total number of data points to calculate the correlation coefficient.
Interpret the correlation coefficient as follows:
- +1 indicates a perfect positive monotonic relationship.
- -1 indicates a perfect negative monotonic relationship.
- 0 suggests no relationship between the variables.
The Spearman test is particularly useful when the data does not meet the assumptions required for Pearson correlation, such as normality or linearity. A high positive Spearman correlation coefficient indicates a strong monotonic relationship between the variables, while a low coefficient suggests little to no relationship.
Spearman Rank Correlation Test for Heteroskedasticity
To identify heteroskedasticity, one can employ the Spearman rank correlation test to examine if there is a correlation between the residuals (errors) of a regression model and the predictor variable(s). Here are the detailed steps for conducting this test:
- Run the regression analysis as usual.
- Inspect the residuals (errors) derived from the regression, representing the differences between the actual and predicted values for each data point.
- Rank the residuals from smallest to largest.
- Rank the values of the predictor variable(s).
- Compute the Spearman rank correlation coefficient between the ranked residuals and the ranked predictor values.
- If the correlation coefficient is statistically significant, it indicates a relationship between the residuals and the predictor variable, suggesting heteroskedasticity.
- If the correlation coefficient is not significant, it provides evidence that heteroskedasticity is not present.
This approach works because heteroskedasticity implies that the residuals' variance changes with the predictor values. By ranking both the residuals and predictor values, any relationship between them is preserved in the ranks. The use of Spearman correlation is effective here since it is a nonparametric test, making it robust to outliers. It can identify a monotonic relationship between the residuals and predictor values, which would indicate the presence of heteroskedasticity.
Spearman Rank Order Correlation Test

The Spearman Rank Order Correlation Test is a statistical method that measures how well a monotonic function describes the relationship between two variables. Unlike the Pearson Correlation, which uses the actual data values, the Spearman test ranks all data points from smallest to largest and uses these ranks for correlation analysis. This approach makes the Spearman test more robust to outliers and deviations from normality assumptions. The test can identify monotonic relationships (where one variable consistently increases or decreases as the other variable does) but cannot detect non-linear relationships.
The main steps in performing the Spearman Rank Order Correlation Test are as follows:
- Assign a rank to each data value from both variables, ranging from 1 to n, where n is the total number of data points. Resolve ties by assigning the average rank.
- Calculate the difference between the ranks for each paired data point (one from each variable).
- Square each difference.
- Sum all the squared differences.
- Calculate the correlation coefficient (ρ) based on the sum of squared rank differences and the total number of data points.
- Analyze the correlation coefficient as follows:
- 1 indicates a perfect positive monotonic relationship.
- -1 indicates a perfect negative monotonic relationship.
- 0 indicates no relationship between the variables.
The main advantage of the Spearman Rank Order Correlation Test is that it does not assume any specific distribution for the raw data and is resistant to outliers. However, some information may be lost when using ranks rather than raw values. This test is a suitable alternative to Pearson correlation when data irregularities are a concern. A significant positive Spearman correlation coefficient indicates a strong monotonic relationship between the two variables.
Monotonic Relationship
A monotonic affinity refers to a relationship between two variables where changes in one variable consistently correspond to changes in the other variable. Specifically, as one variable increases (or decreases), the other variable also consistently increases (or decreases) without any deviations or fluctuations.
Conclusion
The Spearman Rank Correlation Test is a different way to measure the relationship between two variables compared to the Pearson correlation coefficient. It provides a strong test of the direction and strength of a particular relationship using ranks instead of the actual data values. This makes the Spearman test less sensitive to outliers and assumptions like normal distribution. However, because it uses ranks instead of raw data, some information is lost which can reduce its ability to detect relationships. It's important to note that the Spearman test can only identify monotonic relationships and not other types of relationships.
|
157 videos|236 docs|166 tests
|
FAQs on Rank Correlation Test - Crash Course for UGC NET Commerce
| 1. What is the Spearman Rank Correlation Test? |  |
| 2. How is the Spearman Rank Correlation Test helpful in detecting heteroskedasticity? |  |
| 3. What is the difference between Spearman Rank Correlation Test and Spearman Rank Order Correlation Test? |  |
| 4. When should the Spearman Rank Correlation Test be used instead of the Pearson correlation test? |  |
| 5. How does the Spearman Rank Correlation Test help in determining a monotonic relationship between variables? |  |















