Prime Time Chapter Notes | Maths Olympiad Class 6 PDF Download
| Table of contents |

|
| Introduction |

|
| Common Multiples and Common Factors |

|
| Prime Numbers |

|
| Co-prime Numbers for Safe-keeping treasure |

|
| Prime Factorization |

|
| Divisibility Tests |

|
| Fun with Numbers |

|
Introduction
In this chapter, we will explore the world of numbers by understanding how they can be divided and multiplied in various ways. We will learn about prime numbers, composite numbers, and how these concepts help us solve problems in mathematics. By the end of this chapter, you'll be able to identify prime numbers, understand the importance of factors and multiples, and use these concepts to solve puzzles and games.
Common Multiples and Common Factors
- Common Multiples: These are numbers that are multiples of two or more numbers. For example, the common multiples of 3 and 5 are 15, 30, 45, etc. These numbers are special because they can be divided by both 3 and 5 without leaving any remainder.
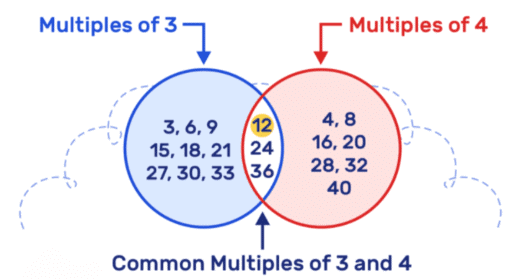
- Common Factors: These are numbers that divide two or more numbers exactly without leaving a remainder. For example, the common factors of 14 and 36 are 1 and 2.
Understanding Common Multiples with an Example
Example: The Idli-Vada Game
Imagine you're sitting in a circle with your friends, and you're all playing a game called "Idli-Vada." The rules are simple:
- The first player says "1," the next says "2," and so on.
- But when it's time to say a number that is a multiple of 3 (like 3, 6, 9...), instead of saying the number, the player says "idli."
- When it’s time to say a number that is a multiple of 5 (like 5, 10, 15...), the player says "vada."
- If a number is a multiple of both 3 and 5 (like 15, 30...), the player says "idli-vada!"

The game continues until someone makes a mistake, and the last person remaining wins.
Understanding the Game: Common Multiples
Now, let's look at what’s happening in the game.
- Multiples of 3: These are numbers like 3, 6, 9, 12... where you say "idli."
- Multiples of 5: These are numbers like 5, 10, 15, 20... where you say "vada."
- Common Multiples of 3 and 5: These are special numbers like 15, 30, 45... where you say "idli-vada" because they are multiples of both 3 and 5.
In the game, when you say "idli" or "vada," you’re recognizing the multiples of 3 and 5. When you say "idli-vada," you're identifying numbers that are shared multiples of both 3 and 5.
Understanding Common Factors with an Example
Example: Jump Jackpot
Now, let’s explore another game called "Jump Jackpot." Here’s how it works:
- Grumpy hides a treasure on a number, say 24.
- Jumpy can only land on multiples of a number he chooses (like 4, 6, or 12).
- To win, Jumpy must land exactly on 24.
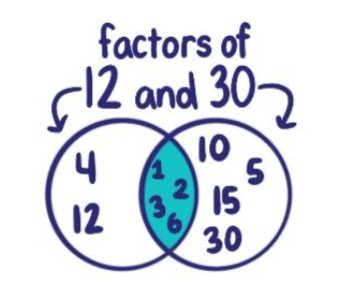
For example, if Jumpy picks 4, he lands on 4, 8, 12, 16, 20, 24... and wins the treasure! If he picks 6 or 12, he also wins because these numbers are factors of 24.
But what if there are two treasures? Let’s say one is on 14 and the other on 36. Jumpy needs to pick a number that will allow him to land on both. If he picks 7, he lands on 14 but misses 36. However, if he picks 2, he lands on both 14 and 36, winning both treasures.
Understanding the Game: Common Factors
In "Jump Jackpot," when Jumpy successfully lands on both treasures, he’s using a common factor.
- Factors of 14: These are numbers like 1, 2, 7, and 14.
- Factors of 36: These are numbers like 1, 2, 3, 4, 6, 9, 12, 18, and 36.
- Common Factors of 14 and 36: These are numbers that can divide both 14 and 36 perfectly, like 1 and 2.
Prime Numbers
- Prime Numbers: A prime number is a number greater than 1 that can only be divided evenly by 1 and itself. For example, 7 is a prime number because the only numbers that divide 7 evenly are 1 and 7.
- Composite Numbers: A composite number is a number that has more than two factors. This means it can be divided evenly by 1, itself, and at least one other number. For example, 12 is composite because it can be divided by 1, 2, 3, 4, 6, and 12.
The number 1 is neither a prime nor a composite number.
Understanding Prime Numbers & Composite Numbers with Examples
Example 1: The Fig Packing Game
Guna and Anshu want to pack figs from their farm. Guna decides to put 12 figs in each box, and Anshu wants to put 7 figs in each box. They start arranging the figs in rectangular shapes:
- Guna's Arrangement: Guna can arrange 12 figs in different ways, like 2 rows of 6 figs each (2 × 6) or 3 rows of 4 figs each (3 × 4). This is because 12 has several factors.


- Anshu's Arrangement: Anshu can only arrange 7 figs in one way: 1 row of 7 figs or 7 rows of 1 fig. This is because 7 has only two factors.

Understanding the Concepts
- Factors: The game shows us that numbers like 12 can be arranged in many ways because they have several factors (e.g., 12 = 2 × 6 or 3 × 4). Numbers like 7, which can only be arranged in one way, have just two factors (1 and the number itself).
- Prime Numbers: Anshu's 7 figs could only be arranged in one way because 7 is a prime number. A prime number has exactly two factors: 1 and the number itself. Examples of prime numbers include 2, 3, 5, 7, 11, and 13.
- Composite Numbers: Guna's 12 figs could be arranged in several ways because 12 is a composite number. A composite number has more than two factors. Examples include 4, 6, 8, 9, and 12.
Example 2: Finding Prime Numbers: The Sieve of Eratosthenes
To find prime numbers between 1 and 100, you can use a method called the Sieve of Eratosthenes: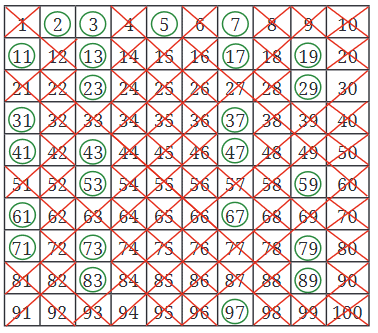
- Cross out 1 because it's neither prime nor composite.
- Circle 2 (the first prime number), then cross out all multiples of 2 (like 4, 6, 8...).
- Circle 3 (the next prime number), then cross out all multiples of 3 (like 6, 9, 12...).
- Circle 5 and cross out all multiples of 5 (like 10, 15, 20...).
- Continue this process until all numbers are either circled or crossed out.
The circled numbers are primes, and the crossed-out numbers (except for 1) are composites. This method helps you quickly find all prime numbers up to 100.
Primes through the Ages
- Prime numbers are like the basic building blocks for all whole numbers. Since ancient times, over 2000 years ago, mathematicians have been trying to understand the mysteries of prime numbers, and they are still working on it today!
- One interesting question is whether there is a largest prime number or if there are an infinite number of them. A famous mathematician named Euclid found the answer to this question a long time ago, and you will learn about it in a later class.
- Here's a fun fact: The largest prime number that anyone has ever written down is so enormous that it would take about 6500 pages to write it out by hand! Because of its size, people can only keep it on a computer.
Co-prime Numbers for Safe-keeping treasure
Co-prime numbers are two numbers that have no common factors other than 1. This means they can't be divided by any of the same numbers except for 1.
Understanding Co-prime with an Example
Imagine you have two friends, Alice and Bob, who love collecting different types of marbles. Alice has a bag with 7 marbles, and Bob has a bag with 9 marbles. They want to share their marbles in equal groups, but there’s a catch: they want to make sure no one group has the same number of marbles from both bags.
Now, let’s see if they can do this. If we try to split the marbles into groups, we notice something interesting: 7 and 9 don’t have any common number of marbles that can divide them equally, except for 1. This means Alice and Bob can’t form groups where both have the same number of marbles.
So, in this case, 7 and 9 are called co-prime numbers because they don’t share any common factors other than 1.
To make it even simpler, think of co-prime numbers as two friends who like different things and don’t have anything in common, except they both like ice cream (which is like the number 1 in this case).
Another example could be 8 and 15. These numbers are also co-prime because there’s no number other than 1 that can evenly divide both 8 and 15. Just like Alice and Bob, these numbers don’t have anything else in common!
Keeping Treasure Safe
Coprime factors are like a secret code for keeping treasures safe. If two numbers don't share any factors other than 1, they are called coprime. This means that if you place treasures on these numbers, someone trying to reach both with the same jump size (other than 1) won't be able to, making it a perfect hiding spot for your treasures!
Co-prime Art
Imagine you have a circle with pegs placed around it, like a clock face. You start by tying a piece of thread to one peg and then skipping a certain number of pegs before tying the thread to the next one. This is called the "thread-gap."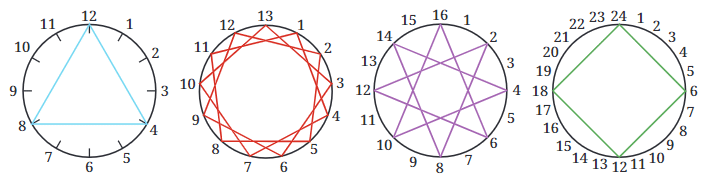
Now, let’s look at some examples to understand how this works:
15 Pegs, Thread-gap of 10:
- Imagine you have 15 pegs in a circle. You tie the thread to the first peg, skip 10 pegs, and tie the thread to the next peg. Then, you keep doing this until you come back to the first peg.
- Since 15 and 10 have common factors (5), the thread will not touch every peg. It will create a pattern where some pegs are skipped.
10 Pegs, Thread-gap of 7:
- Now, you have 10 pegs, and you skip 7 pegs each time you tie the thread.
- 10 and 7 are co-prime (they have no common factors other than 1). So, the thread will eventually touch every peg, creating a complete pattern.
14 Pegs, Thread-gap of 6:
- Here, you have 14 pegs and skip 6 pegs each time.
- Since 14 and 6 share common factors (2), the thread will not touch every peg, and some pegs will be skipped in the pattern.
8 Pegs, Thread-gap of 3:
- You have 8 pegs and skip 3 pegs each time.
- 8 and 3 are co-prime, so the thread will eventually touch every peg, making a full pattern.
What’s Happening Here?
When the number of pegs and the thread-gap are co-prime (like 10 and 7 or 8 and 3), the thread will touch every peg, creating a complete pattern. But when they’re not co-prime (like 15 and 10 or 14 and 6), the thread will skip some pegs, and you won’t get a full pattern.
Prime Factorization
- When we break down a number into its individual factors, those factors are called prime factors if they are prime numbers. For example, the prime factors of 56 are 2 and 7 because both are prime numbers.
- Every number greater than 1 can be broken down into prime factors, a process known as prime factorization. This involves continuously breaking down composite numbers into their factors until only prime numbers are left.
- The number 1 does not have a prime factorization because it is not divisible by any prime number. Prime factorization applies only to numbers greater than 1.
Understanding Prime Factorization with an Example
Imagine you have a bunch of candies, and each candy is a different flavor. Now, you want to divide these candies into smaller groups where each group only has one type of candy.
For example, let’s say you have 56 candies. You start by grouping them into smaller piles:
- First, you notice you can divide them into 14 candies in each pile, and you’ll have 4 piles (14 × 4 = 56).
- Then, you break down one of these piles (14 candies) into 7 candies and 2 candies (7 × 2 = 14).
- Finally, you look at the other pile with 4 candies and see that you can divide it into two groups of 2 candies each (2 × 2 = 4).
Now, you’ve broken down the candies as much as possible, so you have:
- Two piles of 2 candies
- One pile of 7 candies
These numbers—2 and 7—are prime numbers, meaning they can’t be divided into smaller groups of candies anymore. So, the prime factorization of 56 is 2 × 2 × 2 × 7.
Why Is This Important?
Prime factorization is like breaking down a number into its basic building blocks, just like separating candies into groups of the same flavor. Every number (greater than 1) can be broken down this way until you only have prime numbers left.
For example, if you want to know if two numbers, like 56 and 63, are co-prime (which means they have no common factors other than 1), you can look at their prime factorizations:
- 56 = 2 × 2 × 2 × 7
- 63 = 3 × 3 × 7
Here, you see that both numbers share the prime factor 7, so they are not co-prime. They have something in common, just like if two different candy bags had the same flavor.
Why the Order Doesn’t Matter
When you’re multiplying the numbers together to get back to the original number, the order you multiply them in doesn’t change the result.
For example:
- 2 × 3 × 5 = 30
- 5 × 2 × 3 = 30
No matter how you arrange them, multiplying the same numbers will always give you the same total. This is like saying that no matter which order you pick up the candies, you’ll still end up with the same number of candies in the end!
Prime Factorization of a Product of Two Numbers
When we want to find the prime factorization of a number, we start by writing it as a product of two factors. For instance, we can express 72 as 12 x 6.
Understanding with an Example
Imagine you have a big bag of candies, and you want to find out what types of candies are inside by breaking it down into smaller bags. For example, let’s say you have 72 candies. You decide to first split them into two smaller bags, one with 12 candies and another with 6 candies (72 = 12 × 6).
Next, you take a look at each smaller bag:
- The bag with 12 candies can be further split into 2, 2, and 3 candies (12 = 2 × 2 × 3).
- The bag with 6 candies can be split into 2 and 3 candies (6 = 2 × 3).
Now, to find out the original types of candies in the big bag (which is 72), you just combine the candies from both smaller bags:
- 72 = 2 × 2 × 3 × 2 × 3
To make it easier, you can rearrange them like this:
- 72 = 2 × 2 × 2 × 3 × 3
Now, you’ve found out that the big bag of 72 candies is made up of 2’s and 3’s.
Using Prime Factorization to Check if Two Numbers are Co-prime
Understanding with an Example
Let’s say you have two different bags of candies, one with 56 candies and another with 63 candies. You want to check if there’s any common type of candy in both bags, meaning they aren’t co-prime.
You break down the candies in both bags:
- The 56-candy bag is made up of 2 × 2 × 2 × 7 candies.
- The 63-candy bag is made up of 3 × 3 × 7 candies.
When you compare them, you see that both bags have 7 candies. Since they share a common type of candy (which is 7), they are not co-prime.
Let’s try with two other bags, one with 80 candies and another with 63 candies:
- The 80-candy bag is made up of 2 × 2 × 2 × 2 × 5 candies.
- The 63-candy bag is made up of 3 × 3 × 7 candies.
This time, when you compare the two, you see that there are no common types of candies between them. Since they don’t share any common factors, these two numbers (80 and 63) are co-prime!
More Examples
Example 1: Consider two bags, one with 40 candies and another with 231 candies.
- The 40-candy bag is made up of 2 × 2 × 2 × 5 candies.
- The 231-candy bag is made up of 3 × 7 × 11 candies.
- There are no common types of candies between the two bags, so 40 and 231 are co-prime.
Example 2: Consider two other bags, one with 242 candies and another with 195 candies.
- The 242-candy bag is made up of 2 × 11 × 11 candies.
- The 195-candy bag is made up of 3 × 5 × 13 candies.
- Again, there are no common types of candies, so 242 and 195 are also co-prime.
Using Prime Factorization to Check if One Number is Divisible by Another
Understanding with Examples
Think of numbers as baskets filled with fruits, and each type of fruit represents a prime factor. Now, you want to check if one basket (number) can completely fit into another basket without leaving anything out. If all the fruits (prime factors) of the smaller basket fit inside the bigger one, then the bigger number is divisible by the smaller number.
Example 1: Is 168 Divisible by 12?
Let’s say you have a basket with 168 fruits and another basket with 12 fruits. To check if 168 is divisible by 12, we break down the fruits (prime factors) in each basket.
- 168 = 2 × 2 × 2 × 3 × 7
- 12 = 2 × 2 × 3
Now, look at the fruits in both baskets. You can see that all the fruits in the 12-fruit basket (2 × 2 × 3) are also in the 168-fruit basket. This means you can fit the 12-fruit basket inside the 168-fruit basket without leaving anything out.
So, 168 is divisible by 12!
Example 2: Is 75 Divisible by 21?
Now, let’s take a basket with 75 fruits and another basket with 21 fruits.
- 75 = 3 × 5 × 5
- 21 = 3 × 7
When we look at the fruits, we see that the 75-fruit basket has 3 and 5, but it doesn’t have 7, which is in the 21-fruit basket. This means the smaller basket cannot fit inside the bigger one completely.
So, 75 is not divisible by 21.
Divisibility Tests
Divisibility tests are like shortcuts that help you figure out if one number can be divided by another without doing long division. Instead of going through the entire process of dividing, you can use patterns or rules to quickly check.
Divisibility by 10
- To check if a number is divisible by 10, simply look at the last digit.
- If the last digit is a 0, the number is divisible by 10.
Example: Is 8560 divisible by 10?
- Look at the last digit: 0.
- Since it ends in 0, 8560 is divisible by 10.
Divisibility by 5
- For divisibility by 5, the rule is similar but slightly different.
- If the last digit is a 0 or 5, the number is divisible by 5.
Example: Is 8560 divisible by 5?
- Look at the last digit: 0.
- Since it ends in 0, 8560 is divisible by 5.
Divisibility by 2
- A number is divisible by 2 if its last digit is even.
- This means the last digit should be 0, 2, 4, 6, or 8.
Example: Is 8560 divisible by 2?
- Look at the last digit: 0.
- Since it ends in 0 (an even number), 8560 is divisible by 2.
Divisibility by 4
- To check if a number is divisible by 4, look at the last two digits of the number.
- If the number formed by these two digits is divisible by 4, then the whole number is divisible by 4.
Example: Is 8536 divisible by 4?
- Look at the last two digits: 36.
- Since 36 ÷ 4 = 9 (with no remainder), 8536 is divisible by 4.
Divisibility by 8
- For divisibility by 8, check the last three digits of the number.
- If the number formed by these three digits is divisible by 8, then the whole number is divisible by 8.
Example: Is 8560 divisible by 8?
- Look at the last three digits: 560.
- Since 560 ÷ 8 = 70 (with no remainder), 8560 is divisible by 8.
By using these simple patterns, you can quickly check whether a number is divisible by 2, 4, 5, 8, or 10 without needing to do the full division. These rules make it much easier to handle large numbers!
Fun with Numbers
Special Numbers
Let’s take a look at how different numbers can be considered special compared to others. Here’s the first set of numbers:9, 16, 25, 43
Each of these numbers can be seen as special in its own way, depending on how you look at them:
- 9 is special because it’s the only single-digit number. It’s also a perfect square (3 × 3).
- 16 is special because it’s the only even number in the group, and it’s also a perfect square (4 × 4).
- 25 is special because it’s the only number that’s a multiple of 5, and it’s also a perfect square (5 × 5).
- 43 is special because it’s the only prime number, meaning it has no divisors other than 1 and itself. Additionally, it’s the only number in this set that is not a perfect square.
Now, let’s try to find out what makes numbers in the following boxes special:
Box 1: 5, 7, 12, 35
- 5: It’s a prime number and the only number that ends in 5.
- 7: It’s also a prime number.
- 12: It’s the only number that is divisible by 3 (12 = 3 × 4).
- 35: It’s the only number that is a multiple of 7 and 5.
Box 2: 3, 8, 11, 24
- 3: It’s the only single-digit prime number.
- 8: It’s the only even number that is also a power of 2 (2 × 2 × 2).
- 11: It’s the only two-digit prime number.
- 24: It’s the only number that is a multiple of 8.
Box 3: 27, 3, 123, 31
- 27: It’s the only number that is a perfect cube (3 × 3 × 3).
- 3: It’s the only single-digit prime number.
- 123: It’s the only three-digit number.
- 31: It’s a prime number.
Box 4: 17, 27, 44, 65
- 17: It’s a prime number.
- 27: It’s the only number that is a perfect cube (3 × 3 × 3).
- 44: It’s the only even number.
- 65: It’s the only number that is a multiple of 5.
A Prime Puzzle
In this puzzle, the goal is to fill a grid with prime numbers so that the product of each row equals the number on the right, and the product of each column equals the number below it.
Here’s how the puzzle is solved:
Puzzle Grid: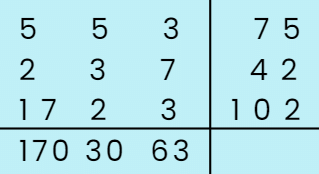
Rules to Solve the Puzzle:
- Prime Numbers Only: Each cell must be filled with a prime number.
- Product of Rows: The product of the numbers in each row must equal the number to the right of that row.
- Product of Columns: The product of the numbers in each column must equal the number below that column.
Example:
- The first row has primes 5, 5, and 3. The product is 5 × 5 × 3 = 75.
- The first column has primes 5, 2, and 17. The product is 5 × 2 × 17 = 170.
By following these rules, you can solve the prime puzzle and ensure that all the conditions are met!
|
34 videos|123 docs|58 tests
|
FAQs on Prime Time Chapter Notes - Maths Olympiad Class 6
| 1. What are common multiples and how are they used in mathematics? |  |
| 2. How do you determine if two numbers are co-prime? |  |
| 3. What is prime factorization and why is it important? |  |
| 4. What are some common divisibility tests for numbers? |  |
| 5. What are prime numbers and how can they be identified? |  |
















