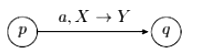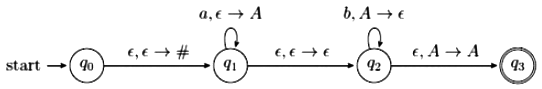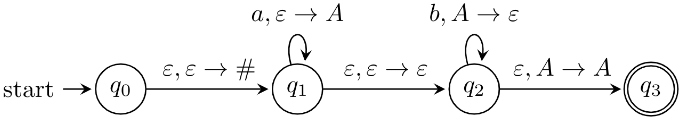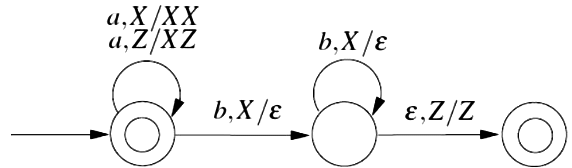Previous Year Questions: Push-down Automata | Theory of Computation - Computer Science Engineering (CSE) PDF Download

Q1: Consider the pushdown automaton (PDA) P below, which runs on the input alphabet {a, b}, has stack alphabet {⊥, A}, and has three states {s, p, q}, with s being the start state. A transition from state u to state v, labelled c/ X / γ , where c is an input symbol or, X is a stack symbol, and γ is a string of stack symbols, represents the fact that in state u, the PDA can read c from the input, with X on the top of its stack, pop X from the stack, push in the string y on the stack, and go to state v. In the initial configuration, the stack has only the symbol in it. The PDA accepts by empty stack.

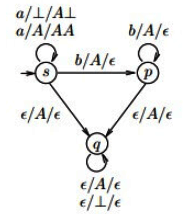
Which one of the following options correctly describes the language accepted by P?  (2023)
(a) {a^mbⁿ |1 ≤ m and n < m}
(b) {a^mbⁿ | 0 ≤ n ≤ m}
(c) {a^mbⁿ | 0 ≤ m and 0 < n}
(d) {a^m | 0 ≤ m} ∪ {bⁿ | 0 ≤ n}
Ans: (a)
Sol:
Only state q empties all the symbols from the stack, so the string must reach to state q in order to get accepted.
Several ways to get into state q are - {a^m | m >1} U {a^mbⁿ | n < m}
combining them we will get,
L(P) = {a^mbⁿ |1< m and n < m}, so option (A) is the answer.

Q2: In a pushdown automaton P = (Q, Σ, Γ, δ, q₀, F), a transition of the form,

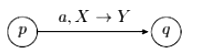
where p, q ∈ Q α ∈ σ ∪ {ϵ}, X, Y, ∈ Γ∪ {ϵ}, represents
(q, Y) ∈ δ(p, a, X)
Consider the following pushdown automaton over the input alphabet ∑ = {a, b} and stack alphabet
Γ = {#, 4}.

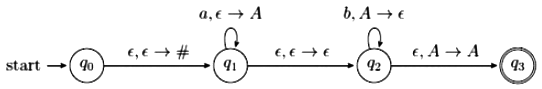
The number of strings of length 100 accepted by the above pushdown automaton is ___________  (2021 SET-1)
(a) 50
(b) 49
(c) 101
(d) 100
Ans: (a)
Sol: 
Correct Answer: 50

A detailed analysis of the given Automaton(skip if you’re comfortable with PDAs):

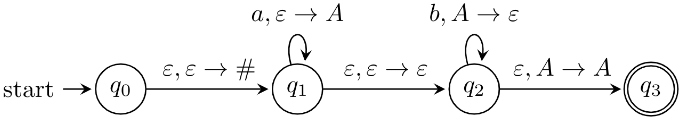
1. PDAs accept strings either by emptying the stack or by reaching the final state after reading the entire input tape. In this example, the transitions from initial state qo 91 is marked by pushing # into the stack and is the only transition that involves # and can't be popped out again. So, there is no chance of acceptance by emptying the stack rather it's only by reaching the final state.
2. a's can only be accepted in state q₁ and b's only by state q₂ this implies the string must be of the form {ab} for now.
3. To read b's from the input tape, we've to pop-out A each time which's obtainable from accepting a's. So, the number b's <a's for all the b's to be accepted in this state.
4. To reach the final state we need at least one A to make the transition to the final state although it's funny about A not being spent.

Note: Reading ϵ from stack doesn’t use up any of the stack contents just like transitions in a conventional FAs.
The given automaton accepts strings of the form {a^mbⁿ, where m ≥ n + 1}. And, it's given the question that m + n = 100.
So the possible set values in the form of (m, n) are {(100, 0), (99, 1),..., (51, 49)} which in total there are 50.
Try for (m = 50, n = 50) to better understand why it isn't accepted.

Q 3: Consider the transition diagram of a PDA given below with input alphabet ∑ = {a, b} and stack alphabet F= {X, Z). Z is the initial stack symbol. Let L denote the language accepted by the PDA.

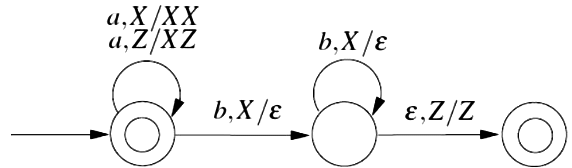
Which one of the following is TRUE?  (2016 SET-1)
(a) L = {aⁿbⁿ ∣ m ≥ 0} is not accepted by any finite automata
(b) L = {aⁿ ∣ n ≥ 0} ∪ {aⁿbⁿ ∣ m ≥ 0} is not accepted by any deterministic PDA
(c) L is not accepted by any Turing machine that halts one very input
(d) L = {aⁿ ∣ n ≥ 0} ∪ {aⁿbⁿ ∣ m ≥ 0} is deterministic context-free
Ans: (d)
Sol:
Strings accepted at I^st final state are aⁿ, n ≥ 0 and strings accepted at II^nd final state are aⁿbⁿ, n ≥ 0 (actually n ≥ 1 at this state, n = 0 already included at first state).
L = {aⁿ | n ≥ 0} ∪ {aⁿbⁿ | n ≥ 0}
Language is deterministic context-free accepted by DPDA (dpda is already given) and so by TM too, and not regular (as we need stack to implement it), and so cannot accepted by FA
Correct Answer: D

Q4: Consider the NPDA (Q = {q₀,q₁,q₂}, Σ = {0, 1}, Г = {0, 1, 1}, δ, q₀, q₁, F = {q₂}), where (as per usual convention) Q is the set of states, ∑ is the input alphabet, Г is the stack alphabet, δ is the state transition function, q₀ is the initial state, ⊥ is the initial stack symbol, and F is the set of accepting states.  (2015 SET-1)
The state transition is as follows:

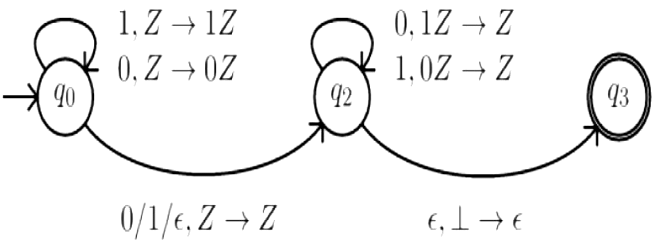
Which one of the following sequences must follow the string 101100 so that the overall string is accepted by the automaton?
(a) 10110
(b) 10010
(c) 01010
(d) 01001
Ans: (b)
Sol:
Here, Z is used to represent the entire stack content except the top
Z is the string in Stack read from top to bottom. 1, Z → 1Z means, on input symbol 1, the stack content changes from Z to 1Z
In qo state, for '1', a '1' is pushed and for a '0' a '0' is pushed. In q₁ state, for a '0' a '1' is popped and for a '1' a '0' is popped. So, the given PDA is accepting all strings of of the form x0x'_r or x1x'_r or xx'_r, where x'_r is the reverse of the 1's complement of 2. i.e.:

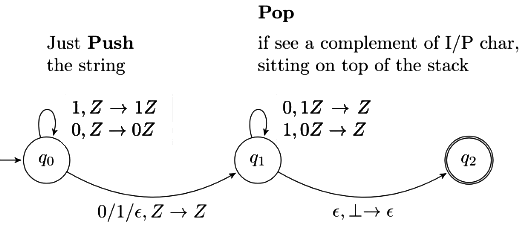
The given string 101100 has 6 letters and we are given 5 letter strings. So, x0 is done, with x = 10110.
So, x'_r = (01001)_r = 10010.
Answer is option B.