Important Formulas: Fractions | Mathematics for Class 6 PDF Download
1. Fraction: A fraction represents a part of a whole. If you divide something (like a pizza) into equal parts, each part is called a fraction of the whole.
2. Fractional Unit: A fractional unit refers to one part of the whole when it’s divided equally. It tells us what fraction of the whole one part is.
Example: In the fraction 1/5, the fractional unit is 1 part out of 5 equal parts.
3. Reading Fractions
- Numerator: The number on top of the fraction, which tells how many parts you have.
- Denominator: The number at the bottom, which tells how many equal parts the whole is divided into.

4. Number Line
- A number line can be used to show fractions. Each fraction is a point between whole numbers. The distance between 0 and 1 is divided into equal parts based on the denominator.
- Example: On a number line, 1/2 is halfway between 0 and 1, while 3/4 is closer to 1.
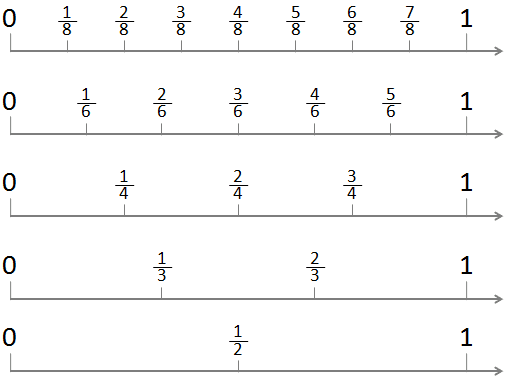
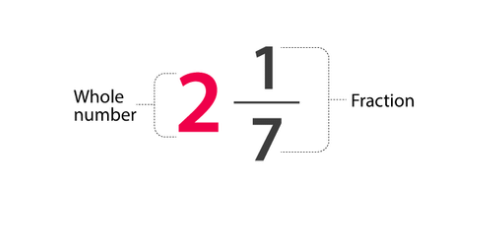
5. Mixed Fractions: A mixed fraction is a combination of a whole number and a fraction.
6. Equivalent Fractions
- Fractions that represent the same part of a whole but look different are called equivalent fractions.
- Method: Multiply or divide both the numerator and denominator by the same number to find equivalent fractions.
- Example: 1/2 is equivalent to 2/4 because if you multiply both the numerator and denominator of 1/2 by 2, you get 2/4.
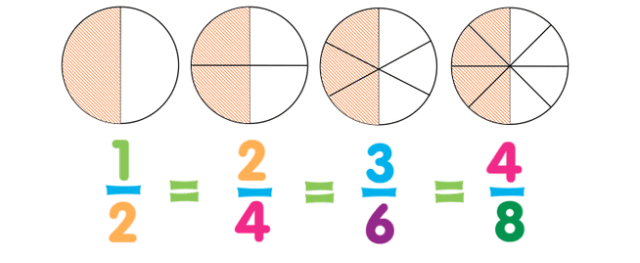
7. Simplest Form
- A fraction is in its simplest form when the numerator and denominator have no common factors other than 1.
- Method: Divide the numerator and denominator by their greatest common divisor (GCD).
- Example: To simplify 6/9, divide both by 3, so the simplest form is 2/3.
8. Comparing Fractions
- Method: To compare fractions, convert them to have the same denominator or use a number line.
Example: To compare 4/5 and 7/9, follow these steps. We can see that 4/5 is greater than 7/9.
(i) Find a common denominator:
- The denominators here are 5 and 9. The least common multiple (LCM) of 5 and 9 is 45.
(ii) Convert the fractions:
- Multiply both the numerator and denominator of 4/5 by 9:
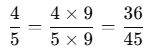
- Multiply both the numerator and denominator of 7/9 by 5:
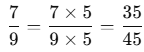
9. Addition of Fractions with same or different denominators
- If the denominators are the same, just add the numerators.
Example: 1/4 + 1/4
Sol: Since the numerators are Add the numerators: 1 + 1 = 2, so the answer is 2/4, which simplifies to 1/2.

- If the denominators are different, find the Least Common Denominator (LCD), then add the numerators.
Example :  +
+ 
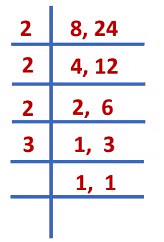
The given fractions are unlike fractions, so we first find LCM of their denominators.LCM of 8 and 24 = 2 × 2 × 2 × 3 = 24
Now, we convert the fractions into like fractions.
(Changing the denominator of fractions to 24)
=
and
+
= =
10. Subtraction of Fractions with same or different denominators
- If the denominators are the same, just subtract the numerators.

- If the denominators are different, find the Least Common Denominator (LCD), then add the numerators.
- Example: For 3/4 - 2/4, subtract the numerators: 3-2 = 1, so the answer is 1/4.
Example : Subtract 4/7 from 8/3.
Solution: 4/7 and 8/3 are unlike fractions as they have different denominators.
So, first we find the LCM of 3 and 7.LCM (3, 7) = 21
8/3 = (8 × 7) / (3 × 7) = 56/21
4/7 = (4 × 3) / (7 × 3) = 12/21
So, we have
8/3 - (4/7)
= 56/21 - (12/21)
= 56/21 - 12/21
= (56 - 12)/21
= 44/21
Answer: 8/3 - (4/7) = 44/21
|
48 videos|334 docs|23 tests
|
FAQs on Important Formulas: Fractions - Mathematics for Class 6
| 1. What are fractions and how are they represented? |  |
| 2. How do you add fractions with different denominators? |  |
| 3. What is the process for subtracting fractions? |  |
| 4. How can fractions be simplified? |  |
| 5. What is the difference between proper and improper fractions? |  |