Unit Test (Solutions): Circles | Mathematics (Maths) Class 10 PDF Download

Q1: A circle has a number of tangents equal to (1 Mark)

(a) 0
(b) 1
(c) 2
(d) Infinite

Ans: (d)

A circle has infinitely many tangents, touching the circle at infinite points on its circumference.

Q2: If the angle between two radii of a circle is 110º, then the angle between the tangents at the ends of the radii is: (1 Mark)

(a) 90º
(b) 50º
(c) 70º
(c) 40º

Ans: (c)

If the angle between two radii of a circle is 110º, then the angle between tangents is 180º − 110º = 70º. (By circles and tangents properties)

Q3: If a parallelogram circumscribes a circle, then it is a ______________________.

Ans: Rhombus

If a parallelogram circumscribes a circle, then it is a Rhombus.

Q4: Two concentric circles are of radii 5 cm and 3 cm. The length of the chord of the larger circle which touches the smaller circle is:

(a) 8 cm
(b) 10 cm
(c) 12 cm
(d) 18 cm

Ans: (a)

As per the given question: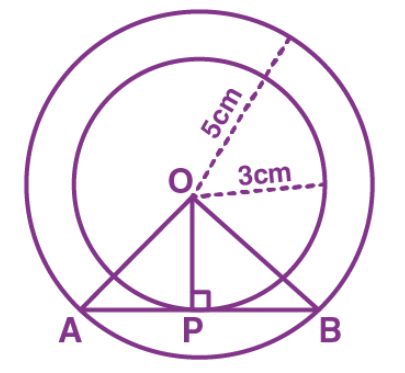 

From the above figure, AB is tangent to the smaller circle at point P.

∴ OP ⊥ AB

By Pythagoras theorem, in triangle OPA

OA² = AP² + OP²

⇒ 5² = AP² + 3²

⇒ AP² = 25 – 9

⇒ AP = 4

Now, as OP ⊥ AB,

Since the perpendicular from the center of the circle bisects the chord, AP will be equal to PB.

So, AB = 2AP = 2 × 4 = 8 cm

Q5: What is a secant? (1 Mark)

Ans: A line intersecting a circle in two points is called a Secant.

Q6: If PS and PT are tangents from an external point P such that PS = 10 cm and ∠SPT = 60°. Find the length of chord ST. (2 Marks)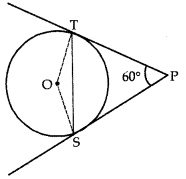

Ans: As tangents from external point are equal in length.

∴ PT = PS

⇒ Triangle PST is isosceles triangle.

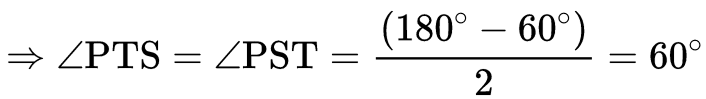⇒ ∆PST is equilateral.
∴ PS = PT = ST
∴ ST = 10 cm. 

Q7: In the given figure, O is the centre of the circle, PT is the tangent and PAB is the secant passing through centre O. If PT = 8 cm and PA = 4 cm, then find the radius of the circle. (2 Marks)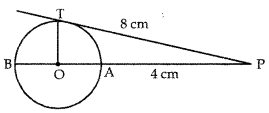

Ans: Let x be the radius of circle.
⇒ OT = OA = X
PO = 4 + x
OT ⊥ PT
∆OTP is rt. ∠d at T.
∴ OP² = OT² + TP²
⇒ (4 + x)² = x² + 64
⇒ 16 + x² + 8x = x² + 64
⇒ 8x = 48
⇒ x = 6 cm. 

Q8: A circle touches the side BC of a ∆ABC at P, and touches AB and AC produced at Q and R respectively as shown in fig. Show that AQ = 1/2 (Perimeter of ∆ABC).  (2 Marks)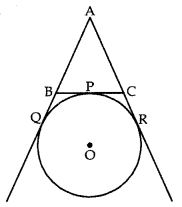

Ans: Since, lengths of tangents drawn from an external point to a circle are equal.
∴ AQ = AR ………… (i)
BP = BQ ………… (ii)
CP = CR …………. (iii)
Perimeter of ∆ABC = AB + BC + CA
= AB + BP + PC + AC
= AB + BQ + CR + AC
(∵ of (ii) and (iii))
= AQ + AR = 2AQ (∵ of (i)) 

⇒ AQ = 1/2 (Perimeter of ∆ABC)

Q9: In figure, AP and BP are tangents to a circle with centre O, such that AP = 5 cm and ∠APB = 60° Find the length of chord AB.  (3 Marks)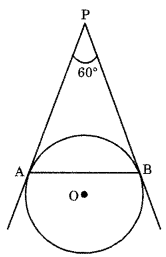

Ans: As the lengths of the tangents drawn from an external point to a circle are equal.
∴ PA = PB
In ∆PAB, sides PA and PB are of the same length.
Hence, ∆PAB is isosceles, with PA = PB and ∠PAB = ∠PBA = x (say).
It is given that
∠APB = 60°
In ∆PAB
∠PAB + ∠PBA + ∠APB =180°
[Angle sum property of A]
∴ x + x + 60° = 180°
⇒ 2x = 120°
⇒ x = 60°
Thus, ∠PAB = ∠PBA = ∠APB = 60°
⇒ ∆PAB is equilateral with AP = BP = AB
It is given that AP = 5 cm
∴ AB = AP = 5 cm
Thus, the length of the chord AB is 5 cm. 

Q10: ABC is a right-angled triangle, right angled at B and with BC = 6 cm and AB = 8 cm. A circle with centre O and radius x has been described in AABC. Find the values of x. (3 Marks)

Ans: We know that radius is perpendicular to tangent.
PO ⊥ BC and OQ ⊥ AB
∴ OPBQ is a rectangle.
But OP = OQ = x 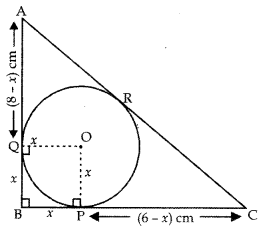OPBQ is a square
Now, BP = x
∴ PC = (6 – x) cm
∴ OP = QB = x
∴ AQ (8 – x) cm
and PC = CR = (6 – x) cm
Now, AC = √AB²+BC²(By Pythagoras Theorem)
= √8²+6² = √64 +36= √100
= 10 cm
AC = AR + CR
10 = (8 – x) + (6 – x)
10 = 14 – 2x
2x = 4cm
x = 2 cm 

Q11: In figure, O is the centre of a circle of radius 5 cm. T is a point such that OT = 13 cm and OT intersects circle at E. If AB is a tangent to the circle at E, find the length of AB, where TP and TQ are two tangents to the circle. (3 Marks)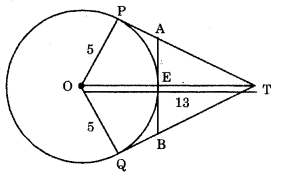

Ans: From the given figure, we have TP = TQ
[∴ Tangents, drawn form an external point to a circle, have equal length.]
and ∠TQO = ∠TPO = 90°
[∵ Tangent to a circle is perpendicular to the radius through the point of contact]
In ∆ TOQ,
QT² + OQ² = OT²
⇒ QT² = 13² – 5² = 144
⇒ QT = 12 cm
Now, OT – OE = ET
= 13 – 5 = 8 cm
Let QB = x cm
∴ QB = EB = x
[∵ Tangents, drawn from an external point to a circle, have equal length.]
Also, ∠OEB = 90°
[Tangent to a circle is perpendicular to the radius through the point of contact.]
In ∆TEB EB² + ET² = TB²

⇒ x² + 8² = (12 – x)²
⇒ x² + 64 = 144 + x² – 24x
⇒ 24x = 80 

⇒ x = 80/24

⇒ x = 10/3

AB = 2x = 2(10/3)cm
∴ Thus, the length of AB is 20/3 cm.

Q12: In the adj oining figure from an external point P, a tangent PT and a line segment PAB is drawn to a circle with centre O. ON is perpendicular on the chord AB. Prove that (5 Marks)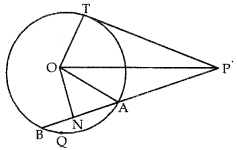
(i) PA.PB = PN² – AN²
(ii) PN² – AN² = OP² – OT²
(iii) PA.PB = PT²
Ans:
Observe that PA = PN – AN and PB = PN + BN
(i) ∴ PA. PB = (PN – AN) (PN + BN)
= (PN – AN) (PN + AN)
[AN = BN as perpendicular from centre bisects the chord] 

= PN² – AN² ……………… (i)

(ii) In right ∆ONP,
OP² = ON² + NP² ⇒ NP²
= OP² – ON² ………….. (a)
and in right ²ONA,
ON² + AN² = OA² ………….. (b)
∴ PN² – AN² = (OP² – ON²) – AN² [using (a)]
= OP² – (ON² + AN²)
= OP² – OA² [using (b)] …………….. (ii)
= OP² – OT² [∵ OA = OT]

(iii) From (i) and (ii)
⇒ PA. PB = OP² – OT² = PT²
[in right ∠d ∆, OP² = OT² + PT²].

Q13: From point P outside the circle, with centre O, tangents PA and PB are drawn in the adjoining fig. If OP is equal to the diameter of the circle, prove that PAB is an equilateral triangle. (5 Marks)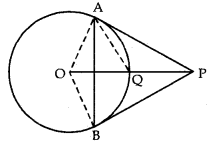

Ans: Let us join OA, OB, AQ
Now, OP = 2OQ [∵ Diameter = 2 Radius]
⇒ OQ = PQ …….. (i)
or Q is mid-point of OP.
Also, OA ⊥ PA [Radius ⊥ tangent through the point of contact]
∆OAP is a right angled triangle.
Q is mid-point of hypotenuse OP.
⇒ QA = OQ = PQ
[As mid-point of hypotenuse of a right triangle is equidistant from three vertices] …… (ii)
But OQ = OA [Radii of same circle] ……. (iii)
(ii) and (iii)
⇒ OA = OQ = QA
⇒ ∆OAQ is an equilateral triangle.
⇒ ∠AOQ = 60°
But in ∆OAP,
∠APO + ∠OAP + ∠AOP = 180°
⇒∠APO + 90° + 60° = 180° [∴ ∠AOQ = ∠AOP = 60°]
⇒ ∠APO = 180° – 150° = 30° Similarly we show that,
∠BPO = 30°
⇒ ∠APB = ∠APO + ∠BPO
= 30°+ 30° = 60° …(iv)
Also in ∆APB,
PA = PB
[Tangents from external point P]
∠PAB = ∠PBA ………….. (v)
In ∆APB, using angle sum property of triangle.
∠PAB + ∠PBA + ∠APB = 180°
⇒ 2∠PAB + 60° = 180°
⇒ 2∠PAB = 180° – 60° = 120°
⇒ ∠PAB = 60° ………….. (vi)
(iv), (v) and (vi)
⇒ ∠APB = ∠PAB = ∠PBA = 60° each.
⇒ ∆PAB is an equilateral ∆.