Unit Test (Solutions): Areas Related to Circles | Mathematics (Maths) Class 10 PDF Download
Time: 1 hour
M.M. 30
Attempt all questions.
- Question numbers 1 to 5 carry 1 mark each.
- Question numbers 6 to 8 carry 2 marks each.
- Question numbers 9 to 11 carry 3 marks each.
- Question number 12 & 13 carry 5 marks each.
Q1: If the perimeter of the circle and square are equal, then the ratio of their areas will be equal to: (1 Mark)
(a) 14:11
(b) 22:7
(c) 7:22
(d) 11:14
Ans: (a)
Given,
The perimeter of circle = perimeter of the square
2πr = 4a
a=πr/2
Area of square = a2 = (πr/2)2
A circle/A square = πr2/(πr/2)2
= 14/11
Q2: The area of the circle that can be inscribed in a square of side 8 cm is (1 Mark)
(a) 36 π cm2
(b) 16 π cm2
(c) 12 π cm2
(d) 9 π cm2
Ans: (b)
Given,
Side of square = 8 cm
Diameter of a circle = side of square = 8 cm
Therefore, Radius of circle = 4 cm
Area of circle
= π(r)2
= π (4)2
= 16π cm2
Q3: The area of a sector of a circle with radius 6 cm if the angle of the sector is 60°. (1 Mark)
(a) 142/7
(b) 152/7
(c) 132/7
(d) 122/7
Ans: (c)
Angle of the sector is 60°
Area of sector = (θ/360°) × π r2
∴ Area of the sector with angle 60° = (60°/360°) × π r2 cm2
= (36/6) π cm2
= 6 × (22/7) cm2
= 132/7 cm2
Q4: In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. The area of the sector formed by the arc is: (1 Mark)
(a) 200 cm2
(b) 220 cm2
(c) 231 cm2
(d) 250 cm2
Ans: (c)
The angle subtended by the arc = 60°
So, area of the sector = (60°/360°) × π r2 cm2
= (441/6) × (22/7) cm2
= 231 cm2
Q5: If the area of a circle is 154 cm2, then its perimeter is (1 Mark)
(a) 11 cm
(b) 22 cm
(c) 44 cm
(d) 55 cm
Ans: (c)
Given,
Area of a circle = 154 cm2
πr2 = 154
(22/7) × r2 = 154
r2 = (154 × 7)/22
r2 = 7 × 7
r = 7 cm
Perimeter of circle = 2πr = 2 × (22/7) × 7 = 44 cm
Q6: What is the area of a circle whose circumference is 44 cm? (2 Marks)
Ans: Circumference of a circle = 2πr
From the question,
2πr = 44
Or, r = 22/π
Now, area of circle = πr2 = π × (22/π)2
So, area of circle = (22×22)/π = 154 cm2
Q7: Find the area of the sector of a circle with a radius of 4 cm and of angle 30°. Also, find the area of the corresponding major sector (Use π = 3.14) (2 Marks)
Ans: Let OAPB be the sector.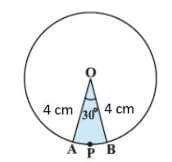
Area of sector = (θ / 360) × πr²
= (30 / 360) × 3.14 × (4)²
= (1 / 12) × 3.14 × 4 × 4
= (1 / 3) × 3.14 × 4
= (12.56 / 3) cm²
= 4.19 cm²
Area of the major sector = [(360 – θ)/ 360] × πr2
= [(360 – 30)/360] × 3.14 × 4 × 4
= (330/360) × 3.14 × 16
= 46.05 cm2
= 46.1 cm2 (approx)
Q8: Calculate the area of a sector of angle 60°. Given, the circle has a radius of 6 cm. (2 Marks)
Ans: Given,
The angle of the sector = 60°
Using the formula,
The area of sector = (θ/360°) ×π r2
= (60°/360°) × π r2 cm2
Or, area of the sector = 6 × 22/7 cm2 = 132/7 cm2
Q9: Calculate the perimeter of an equilateral triangle if it inscribes a circle whose area is 154 cm2 (3 Marks)
Ans: Here, as the equilateral triangle is inscribed in a circle, the circle is an incircle.
Now, the radius of the incircle is given by,
r = Area of triangle/semi-perimeter
In the question, it is given that area of the incircle = 154 cm2
So, π × r2 = 154
Or, r = 7 cm
Now, assume the length of each arm of the equilateral triangle to be “x” cm
So, the semi-perimeter of the equilateral triangle = (3x/2) cm
And, the area of the equilateral triangle = (√3/4) × x2
We know, r = Area of triangle/semi-perimeter
So, r = [x2(√3/4)/ (3x/2)]
=> 7 = √3x/6
Or, x = 42/√3
Multiply both numerator and denominator by √3
So, x = 42√3/3 = 14√3 cm
Now, the perimeter of an equilateral triangle will be = 3x = 3 × 14√3 = 72.7 cm
Q10: Find the Radius of a circle whose Circumference is equal to the sum of the circumferences of two circles of radii 15 cm and 18 cm. (3 Marks)
Ans:
Radius of the first circle = r1 = 15 cm
Radius of the second circle = r2 = 18 cm
∴ Circumference of the first circle = 2πr1 = 30π cm
Circumference of the second circle = 2πr2 = 36π cm
assume, the radius of the circle = R
As per the question,
Circumference of circle = Circumference of the first circle + Circumference of the second circle
2πR= 2πr1+ 2πr2
⇒ 2πR = 30π + 36π
⇒ 66π ⇒ R = 33
⇒ Radius = 33 cm
Hence, the required radius of a circle is 33 cm.
Q11: A chord of a circle of radius 15 cm subtends an angle of 60° at the centre. Find the areas of the corresponding minor and major segments of the circle. (Use π = 3.14 and √3 = 1.73)
Ans: 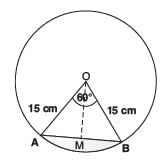 Radius of the circle = 15 cm
Radius of the circle = 15 cm
Central angle subtends by chord = 600
Area of sector = 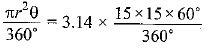
= 117.75 cm2
Area of the triangle formed by radii and chord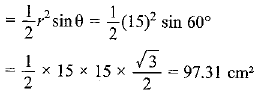
Area of the minor segment = Area of the sector -Area of the triangle formed by radii and chord
= 117.75-97.31 =20.44 cm2
Area of the circle = πr2
= 3.14 x 15 x 15 = 706.5 cm2
Area of the major segment = Area of the circle - Area of the minor segment
= 706.5 - 20.44 = 686.06 cm2
Q12: A chord of a circle of Radius 10 cm subtends a right angle at the center. Find the Area of the corresponding: (5 Marks)
(i) minor segment
(ii) major sector. (Use π = 3.14)
Ans:
AB is the chord that subtends an angle of 90° at the center O.
It is seen that the radius (r) of the circle = 10 cm
(i) Area of the minor sector = (90/360°) × πr2
= (1/4) × (22/7) × 102
Or, Area of the minor sector = 78.5 cm2
Also, the Area of the ΔAOB = 1/2 × OB × OA
Where, OB and OA are the radii of the circle i.e., = 10 cm
Thus, the Area of ΔAOB = 1/2×10×10
= 50 cm2
Then, Area of minor segment = area of the minor sector – Area of ΔAOB
= 78.5 – 50
= 28.5 cm2
(ii) Area of the major sector = Area of circle – Area of minor sector
= (3.14×102) - 78.5
= 235.5 cm2
Q13: A chord of the circle of Radius 15 cm makes the angle of 60° at the center. Find out the areas for the corresponding minor and the major segments of the circle. (Use π = 3.14 and √3 = 1.73) (5 Marks)
Ans:
We know that
Radius = 15 cm
θ = 60°.
Hence,
The Area of the sector OAPB = (60°/360°) × πr2 cm2
= 225/6 πcm2.
Then, ΔAOB is equilateral as two sides are the circle’s radii and,
Therefore, equal, and one angle is 60°.
So, the Area of ΔAOB = (√3/4) ×a2
And (√3/4) ×152
∴ Area of ΔAOB = 97.31 cm2.
Then, the Area of minor segment APB = Area of OAPB – Area of ΔAOB
And, area of minor segment APB = ((225/6)π – 97.31) cm2 = 20.43 cm2
Or
The Area of major segment = Area of the circle – Area of segment APB
And area of major segment = (π×152) – 20.4 = 686.06 cm2
|
127 videos|584 docs|79 tests
|
FAQs on Unit Test (Solutions): Areas Related to Circles - Mathematics (Maths) Class 10
| 1. What is the formula to calculate the area of a circle? |  |
| 2. How do you find the circumference of a circle? |  |
| 3. What is the relationship between the radius and diameter of a circle? |  |
| 4. Can you explain what a sector of a circle is? |  |
| 5. What is the significance of π (pi) in circle geometry? |  |





















