Unit Test (Solutions): Surface Areas and Volumes | Mathematics (Maths) Class 10 PDF Download
Time: 1 hour
M.M. 30
Attempt all questions.
- Question numbers 1 to 5 carry 1 mark each.
- Question numbers 6 to 8 carry 2 marks each.
- Question numbers 9 to 11 carry 3 marks each.
- Question number 12 & 13 carry 5 marks each.
Q1: Two identical solid cubes of side a are joined end to end. Then the total surface area of the resulting cuboid is (1 Mark)
(a) 12a2
(b) 10a2
(c) 8a2
(d) 11a2
Ans: (b)
The total surface area of a cube having side a = 6a2
If two identical faces of side a are joined together, then the total surface area of the cuboid so formed is 10a2.
Q2: A right circular cylinder of radius r cm and height h cm (h>2r) just encloses a sphere of diameter (1 Mark)
(a) r cm
(b) 2r cm
(c) h cm
(d) 2h cm
Ans: (b)
Radius of cylinder = r
Height = h > 2r
Since the sphere is enclosed by a cylinder, the radius of the cylinder will be the radius of the sphere.
Therefore, diameter of sphere = 2r cm
Q3: If we join two hemispheres of same radius along their bases, then we get a; (1 Mark)
(a) Cone
(b) Cylinder
(c) Sphere
(d) Cuboid
Ans: (c)
If we join two hemispheres of same radius along their bases, then we get a Sphere.
Q4: The radius of the top and bottom of a bucket of slant height 35 cm are 25 cm and 8 cm. The curved surface of the bucket is _________________________________. (1 Mark)
Ans: 3630 sq.cm
Curved surface of bucket = π(R1 + R2) x slant height (l)
Curved Surface = (22/7) x (25 + 8) x 35
CSA = 22 x 33 x 5 = 3630 sq.cm.
Q5: If a cone is cut parallel to the base of it by a plane in two parts, then the shape of the top of the cone will be a: (1 Mark)
(a) Sphere
(b) Cube
(c) Cone itself
(d) Cylinder
Ans: (c)
If we cut a cone into two parts parallel to the base, then the shape of the upper part remains the same.
Q6: 2 cubes each for the volume of 64 cm3 are joined end to end. Find out the surface area of the resulting cuboid. (2 Marks)
Ans: Given that,
The Volume (V) for each cube is = 64 cm3
This implies that a3 = 64 cm3
The side for the cube, i.e., a = 4 cm
And the breadth and length of the resulting cuboid will be 4 cm each, while its height will be 8 cm.
Thus, the surface area of the cuboid (TSA) = 2(lb + bh + lh)
On putting the values, we observe,
= 2(8×4 + 4×4 + 4×8) cm2
= (2 × 80) cm2
Therefore, TSA of the cuboid = 160 cm2
Q7: A cubical block of the side 7 cm is surmounted with a hemisphere. What is the greatest diameter the hemisphere could have? Find out the surface area of the solid. (2 Marks)
Ans: It is given that each side for the cube is 7 cm.
The diameter of the circle = side of the cube = 7 cm.
Hence, the radius will be 7/2 cm.
We get,
The total surface area of the solid (TSA) = surface area of the cubical block + CSA for the hemisphere – area of the base of the hemisphere
So, TSA of the solid = 6×(side)2 + 2πr2 - πr2
= 6 × (side)2 + πr2
= 6 × (7)2 + (22/7) × (7/2) × (7/2)
= (6×49) + (77/2)
= 294+38.5 = 332.5 cm2
Hence, the surface area of the solid is 332.5 cm2
Q8: Two cones have their heights in the ratio of 1 : 3 as well as radii in the ratio of 3: 1. What is the ratio for their volumes? (2 Marks)
Ans: Given that,
Ratio for the heights of two cones = 1:3
Ratio for the radii = 3:1
Let h and 3h be the height of the two cones.
And, 3r and r be the corresponding radii for the cones.
Hence, r1 = 3r, h1 = h, r2 = r, h2 = 3h.
Ratio for the volumes = [(1/3)πr12h1]/ [(1/3)πr22h2]
= [(3r)2 h]/[r2 (3h)]
= (9r2h)/(3r2h)
= 3/1
Thus, the ratio of volumes = 3:1
Q9: Water is flowing at the rate of 15 km/h passing through a pipe of the diameter of 14 cm into a cuboidal pond which is 50 m long and 44 m wide. At what time will the level for the water in the pond rise by 21 cm? (3 Marks)
Ans: Assume time taken by pipe to fill pond = t hours
Water flows 15 km in 1 hour, so it will flow 15t metres in t hours.
We get, volume of the cuboidal pond up to the height of 21 cm = volume of the water that passes through the pipe in “t” hours
Considering cuboidal pond,
For the Length, l = 50 m
For the Breadth, b = 44 m
For the Height, h = 21 cm = 0.21 m
We get,
Volume of the tank = lbh
Volume of the water = 50(44)(0.21) = 462 m3
Considering cylindrical pipe
For the Base diameter = 14 cm
For the Base radius, r = 7 cm = 0.07 m
For Height, h = 15t km = 15000t m
We get,
Volume of the cylinder = πr2h
Volume of the water passed in pipe = π(0.07)2(15000t)
=22/7 × 0.07 × 0.07 × 15000t
= 231t cm3
Thus, we have
231t = 462
t = 2 hours
The time required to fill the tank up to a height of 25 cm is 2 hours.
Q10: A heap of rice is in the form for the cone of diameter of 9 m and height of 3.5 m. Find out the volume of the rice. How much canvas cloth is required to cover the heap only? (3 Marks)
Ans: As per the question,
Consider conical heap,
For the Base Diameter = 9 m
Therefore, for the base radius, r = 4.5 m
For Height, h = 3.5 m
We get,
Slant height,
l = √(r2+h2)
l = √(4.52+3.52)
l = √(20.25+12.25)
l = √32.5
l = 5.7 m
The equation for the volume of cone = 1/3πr2h
We get,
volume of the rice = volume of the conical heap
volume of the rice = 1/3π(4.5)2(3.5) =74.25m3
We also get,
Canvas required to just cover heap = Curved surface area of the conical heap
Curved surface area of the cone = πrl
Thus, the canvas required = π(4.5)(5.7) = 80.61 m2 [appx]
Q11: Rasheed gets a playing top (lattu) as his birthday present, in which, surprisingly, he found no colour on it. He wanted to colour it with his crayons. The top is shaped as like a cone surmounted with a hemisphere. The entire top of 5 cm in height, as well as the diameter of the top, is 3.5 cm. Find out the area he has to colour. (Take π = 22/7) (3 Marks)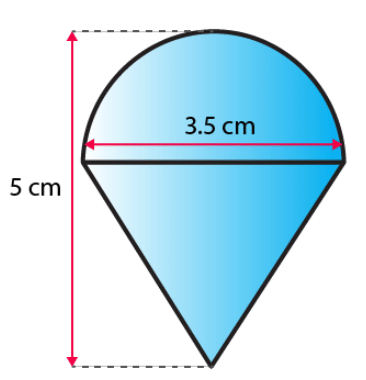
Ans:
TSA for the toy = CSA for the hemisphere + CSA for the cone
Curved surface area of the hemisphere = 1/ 2 (4πr2) = 2πr2 = 2(22/7) × (3.5/2) × (3.5/2) = 19.25 cm2
Height of the cone = height of the top – radius of the hemispherical part
= (5 – 3.5/2) cm = 3.25 cm
Slant height of the cone (l): The slant height l can be found using the Pythagorean theorem:
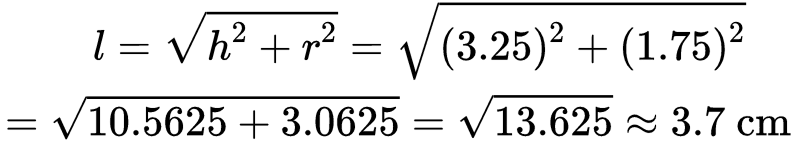
Thus, CSA of cone = πrl = (22/7) × (3.5/2) × 3.7 = 20.35 cm2
So, the surface area of the top = [2(22/7) × (3.5/2) × (3.5/2) + (22/7) × (3.5/2) × 3.7] cm2
= (22/7) × (3.5/2) (3.5+3.7) cm2
= (11/2) × (3.5 + 3.7) cm2
= 39.6 cm2 (approximately)
Q12: Water flows at the rate of 10m/minute and passes through a cylindrical pipe 5 mm in diameter. How long will it take to fill a conical vessel which has a diameter at the base is 40 cm and a depth of 24 cm? (5 Marks)
Ans: Assume the time taken by pipe to fill vessel = t minutes
As water flows 10 m in 1 minute, it will flow 10t meters in t minutes.
As per the question,
Volume of the conical vessel = volume of the water that passes through the pipe in t minutes
Consider the conical pipe,
For the Base Diameter = 40 cm
For the Base radius, r = 20 cm
For Height, h = 24 cm
We know that the volume of the cone = 1/3πr2h
Volume of the conical vessel = 1/3π(20)2(24) = 3200 π cm3
Consider cylindrical pipe,
For the Base diameter = 5 mm = 0.5 cm
For the Base radius, r = 0.25 cm
Water covers 10t m distance in pipe,
So, we get,
For Height, h = 10t m = 1000t cm
We get,
Volume of the cylinder = πr2h
Volume of the water passed in pipe = π(0.25)2(1000t) = 62.5tπ cm3
Hence, we find,
62.5tπ = 3200
62.5t = 3200
t = 51.2 minutes
We get,
0.2 minutes = 0.2(60) seconds = 12 seconds
Hence, t = 51 minutes 12 seconds
Q13: From a solid cylinder those height is 2.4 cm as well as diameter of 1.4 cm. A conical cavity for the same height as well as same diameter is hollowed out. Find out the total surface area of the remaining solid to the nearest cm2. (5 Marks)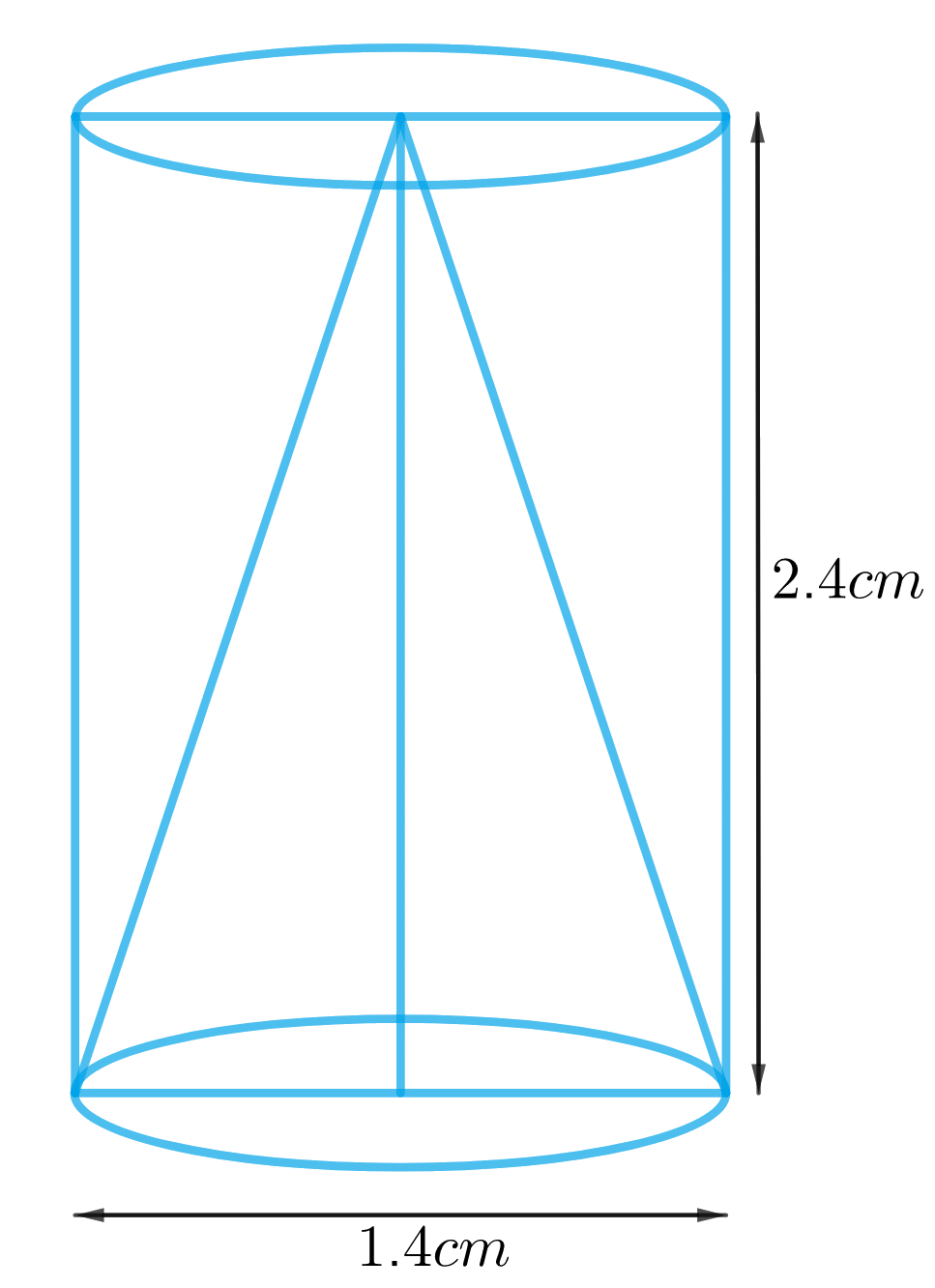
Ans:
From the question we have:
The Diameter of the cylinder = Diameter of the conical cavity = 1.4 cm
Hence, the radius of the cylinder = radius of the conical cavity = 1.4/2 = 0.7
And the height of the cylinder = height of the conical cavity = 2.4 cm
Therefore, Slant height of the conical cavity (l) = √(h2 + r2)
= √(2.42 + 0.72)
= √(5.76 +0.49)
= √(6.25)
= l = 2.5 cm
TSA for the remaining solid = surface area of the conical cavity + TSA for the as the cylinder= πrl+(2πrh + πr2)
= πr(l+2h+r)
= (22/7)× 0.7(2.5+4.8+0.7)
= 2.2×8 = 17.6 cm2
Hence, the total surface area of the remaining solid is 17.6 cm2
|
127 videos|683 docs|84 tests
|
FAQs on Unit Test (Solutions): Surface Areas and Volumes - Mathematics (Maths) Class 10
| 1. What are the basic formulas for calculating the surface area and volume of common geometric shapes? |  |
| 2. How do you derive the formula for the volume of a cylinder? |  |
| 3. What is the difference between surface area and volume? |  |
| 4. Why is understanding surface area and volume important in real-life applications? |  |
| 5. Can surface area and volume formulas be applied to irregular shapes? |  |





















