The Other Side of Zero NCERT Solutions | Mathematics for Class 6 PDF Download
Page 243
Q1: What do you press to go four floors up? What do you press to go three floors down?
Ans: If you press the ‘+’ button once then you will go up one floor and if you press the ‘-‘ button once then you will go down 1 floor.
Hence to go four floors up you must press the ‘+’ button four times which we write as + + + + or +4.
Now to go three floors down you must press the button three times which we write as – – – or -3.
Page 244
Q1: Number all the floors in the Building of Fun. Ans: Let’s mark numbers on all the Floors in the Building of Fun.
Ans: Let’s mark numbers on all the Floors in the Building of Fun.
Page 245
Addition to keep track of movement
Start from the Food Court and press +2 in the lift Where will you reach? _________
Ans: Here, Target floor = Starting floor + Movement
∴ The starting floor is +1 (Food Court) and the number of button presses is +2.
Therefore, floor = starting floor + movement
= (+1) + (+2)
= +3 (Book Store)
Figure it Out
Q1: You start from Floor +2 and press -3 in the lift. Where will you reach? Write an expression for this movement.
Ans: Here, the starting floor is +2 (Art center) and the number of button presses is -3.
Therefore, Target floor = Starting floor + Movement
= (+2) + (-3)
= -1 (Toys Store).
Q2: Evaluate these expressions (you may think of them as Starting Floor + Movement by referring to the Building of Fun).
(a) (+1) + (+4) = _______________
Ans: Here, the starting floor is +1 (Food Court) and the number of button presses is +4.
Therefore, Target floor = Starting floor + Movement
= (+1) + (+4)
= +5 (Sports centre).
(b) (+4) + (+1) = _______________
Ans: Here, the starting floor is +4 (Ice-cream centre) and the number of button presses is +1 (Food court).
Therefore, Target floor = Starting floor + Movement
= (+4) + (+1)
= +5 (Sports centre).
(c) (+4) + (-3) = _______________
Ans: Here, the starting floor is +4 (Ice-cream centre) and the number of button presses is (-3).
Therefore, Target floor = Starting floor + Movement
= (+4) + (-3)
= +1 (Food court).
(d) (-1) + (+2) = _______________
Ans: Here, the starting floor is (-1) (Toys centre) and the number of button presses is +2.
Therefore, Target floor = Starting floor + Movement
= (-1) + 2
= +1 (Food court).
(e) (-1) + (+1) = _______________
Ans: Here, the starting floor is -1 (Toys centre) and the number of button presses is +1.
Therefore, Target floor = Starting floor + Movement
= (-1) + (+1)
= 0 (Welcome Hall means Ground floor).
(f) 0 + (+2) = _______________
Ans: Here, the starting floor is 0 (Ground floor) and the number of button presses is +2.
Therefore, Target floor = Starting floor + Movement
= (0) + (+2)
= +2 (Art centre)
(g) 0 + (-2) = _______________
Ans: Here, the starting floor is 0 (Ground floor) and the number of button presses is -2.
Therefore, Target floor = Starting floor + Movement
= 0 + (-2)
= -2 (Video games).
Q3: Starting from different floors, find the movements required to reach Floor 5. For example, if I start at Floor +2, I must press -7 to reach Floor -5. The expression is (+2) + (-7) = -5. Find more such starting positions and the movements needed to reach Floor -5 and write the expressions.
Ans: (a) If I start at floor +1, 1 must press (-6) to reach floor -5.
The expression is (1) + (-6) = -5.
(b) If I start at floor +3, I must press (-8) to reach the floor (-5).
The expression is (+3) + (-8) = -5.
Page 246
Figure it out
Q: Evaluate these expressions by thinking of them as the resulting movement of combining button presses:
a. (+1) + (+4) = _______________
Ans: Target floor = (+1) + (+4) = +5
b. (+4) + (+1) = _______________
Ans: Target floor = (+4) + (+1) = +5
c. (+4) + (-3) + (-2) = _______________
Ans: Target floor = (+4) + (-3) + (-2)
= 4 + (-5)
= -1
d. (-1) + (+2) + (-3) = _______________
Ans: Target floor = (-1) + (+2) + (-3)
= (-4) + (2)
= -2
Back to Zero!
Q1: Write the inverses of these numbers:
+4, -4, -3, 0, +2, -1
Ans: The additive inverse of +4 = -(+4) = -4.
The additive inverse of -4 = -(-4) = +4.
The additive inverse of -3 = -(-3) = +3.
The additive inverse of zero (0) is zero itself.
The additive inverse of +2 = -(+2) = -2.
The additive inverse of -1 = -(-1) = +1.
Q2: Connect the inverses by drawing lines.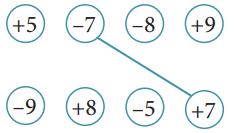 Ans:
Ans: 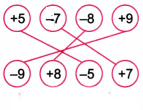
Comparing numbers using floors

Who is on the lowest floor?
1. Jay is in the Art Centre. So, he is on Floor +2.
2. Asin is in the Sports Centre. So, she is on Floor ______.
3. Binnu is in the Cinema Centre. So, she is on Floor ______.
4. Aman is in the toy shop. So, he is on ______.
Ans:  1. Jay is in the Art Centre. So, he is on Floor+2.
1. Jay is in the Art Centre. So, he is on Floor+2.
2. Asin is in the Sports Centre. So, she is on Floor +5.
3. Binnu is in the Cinema Centre. So, she is on Floor -3.
4. Aman is in the toy shop. So, he is on Floor -1.
Page 247
Figure it Out
Q1: Compare the following numbers using the Building of Fun and fill in the boxes with < or >.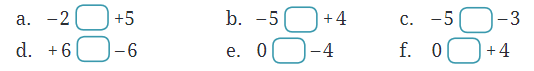
Ans: a. Here, floor -2 is lower than floor +5 then -2 < +5.
b. Here, floor -5 is lower than floor +4 then -5 < +4.
c. Here, floor -5 is lower than floor -3 then -5 < -3.
d. Here, floor +6 is greater than floor -6 then +6 > -6.
e. Here, floor 0 is greater than floor -4 then 0 > -4.
f. Here, floor 0 is lower than floor +4 then 0 < +4.
Q2: Imagine the Building of Fun with more floors. Compare the numbers and fill in the boxes with < or >:
Ans: a. Here, floor -10 is greater than floor -12 then -10 > -12
b. Here, floor +17 is greater than floor -10 then +17 > -10
c. Here, floor 0 is greater than floor -20 then 0 > -20
d. Here, floor +9 is greater than floor -9 then + 9 > -9
e. Here, floor -25 is lower than floor -7 then -25 < -7
f. Here, floor +15 is greater than floor -17 then +15 > -17
Q3: If Floor A = -12, Floor D = -1, and Floor E = +1 in the building shown on the right as a line, find the numbers of Floors B, C, F, G, and H.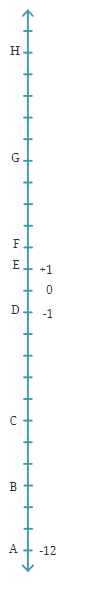 Ans: Let’s mark the numbers on the line.
Ans: Let’s mark the numbers on the line.
0, -1, -2, -3,…………, -12 and 1, 2, 3,……….., 12
Now count each floor, and we get the number of floors.
Here, B = -9, C = -6, F = +2, G = +6 and H = +11
Q4: Mark the following floors of the building shown on the right.
a. -7
b. -4
c. +3
d. -10
Ans: Here, one line is considered as one floor.
The floor above floor 0 is marked with positive numbers and the floor below 0 is numbered with negative numbers.
Now let’s mark the following numbers (-7, -4, +3, -10) in the building by circling the floor.
Page 249
Figure it Out
Complete these expressions. You may think of them as finding the movement needed to reach the Target Floor from the Starting Floor.
a. (+1) – (+4) = _______________
Ans: (+1) – (+4) = -3
b. (0) – (+2) = _______________
Ans: (0) – (+2) = -2
c. (+4) – (+1) = _______________
Ans: (+4) – (+1) = +3
d. (0) – (-2) = _______________
Ans: (0) – (-2) = +2
d. (+4) – (-3) = _______________
Ans: (+4) – (-3) = +7
f. (-4) – (-3) = _______________
Ans: (-4) – (-3) = -1
g. (-1) – (+2) = _______________
Ans: (-1) – (+2) = -3
h. (-2) – (-2) = _______________
Ans: (-2) – (-2) = 0
i. (-1) – (+1) = _______________
Ans: (-1) – (+1) = -2
j. (+3) – (-3) = _______________
Ans: (+3) – (-3) = +6
Page 251
Figure it Out
Complete these expressions. Check your answers by thinking about the movement in the mineshaft.
a. (+40) + _______________ = +200
Ans: Given (+40) + _______________ = +200
Let (+40) + x = +200
⇒ +x = 200 – 40 = 160
∴ (+40) + (+160) = +200
b. (+40) + _______________ = -200
Ans: Given (+40) + _______________ = -200
Let (+40) + x = -200
⇒ x = -200 – 40 = -240
∴ (+40) + (-240) = -200
c. (-50)+ _______________ = +200
Ans: Given (-50) + _______________ = +200
Let (-50) + x = +200
⇒ x = +200 – (-50) = +250
∴ (-50) + (+250) = +200
d. (-50) + _______________ = -200
Ans: Given (-50) + _______________ = -200
Let (-50) + x = -200
⇒ x = -200 – (-50) = -150
∴ (-50) + (-150) = -200
e. (-200) – (-40) = _______________
Ans: Given (-200) – (-40) = _______________
Let (-200) – (-40) = x
⇒ (-200) – (-40) = -160 = x
∴ (-200) – (-40) = -160
f. (+200) – (+40) = _______________
Ans: Given (+200) – (+40) = _______________
Let (+200) – (+40) = x
⇒ +160 = x
∴ (+200) – (+40) = +160
g. (-200) – (+40) = _______________
Ans: Given (-200) – (+40) = _______________
Let (-200) – (+40) = x
⇒ (-200) + (-40) = -240 = x
∴ (-200) + (-40) = -240
Adding, Subtracting, and Comparing any Numbers
Try evaluating the following expressions by similarly drawing or imagining a suitable lift:
(a) -125 + (-30)
(b) +105 – (-55)
(c) +105 + (+55)
(d) +80 – (-150)
(e) +80 + (+150)
(f) -99 – (-200)
(g) -99 + (+200)
(h) +1500 – (-1500)
Ans:
(a) -125 + (-30) = -125 – 30 = -155
(b) +105 – (-55) = 105 + 55 = +160
(c) +105 + (+55) = 105 + 55 = +160
(d) +80 – (-150) = 80 + 150 = +230
(e) +80 + (+150) = 80 + 150 = +230
(f) -99 – (-200) = -99 + 200 = +101
(g) -99 + (+200) = -99 + 200 = +101
(h) +1500 – (-1500) = +1500 + 1500 = 3,000
Page 252
Q: In the other exercises that you did above, did you notice that subtracting a negative number was the same as adding the corresponding positive number?
Ans: Subtracting a number is the same as adding it’s opposite. So subtracting a positive number is like adding a negative number – you move to the left on the number line. Subtracting a negative number is like adding a positive number – you move to the right on the number line.
For example: Subtract -2 – (-3)
Start at -2 and move 3 units to the right.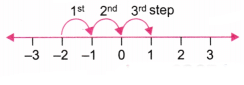 So, -2 – (-3) = +1
So, -2 – (-3) = +1
Q: Take a look at the ‘infinite lift’ above. Does it remind you of a number line? In what ways?
Ans: A number line is a way of representing numbers visually on a straight line. For instance, the number line has arrows at the end to represent this, idea of having no bounds. The symbol used to represent infinity is ∞.
Q: If, from 5 you wish to go over to 9, how far must you travel along the number line?
Page 253 & 254
Q1: Mark 3 positive numbers and 3 negative numbers on the number line above.
Ans: On the Number Line:
Positive numbers: We can mark any three positive numbers, e.g., 3, 6 and 9.
Negative numbers: We can mark any three negative numbers e.g., -2, -5 and -8.
Q2: Write down the above 3 marked negative numbers in the following boxes:
Ans: -2, -5, and -8 are three negative numbers.
Q3: Is 2 > -3? Why? Is -2 < 3? Why?
Ans: Is 2 > -3?
Yes, 2 is a positive number and -3 is a negative number. We know that positive numbers are always greater than negative numbers.
Hence, 2 is greater than -3.
Is -2 < 3? Why?
∴ Yes, -2 is less than 3 because -2 is a negative number and 3 is a positive number.
Hence -2 < 3.
Q4: What are
(i) -5 + 0
(ii) 7 + (-7)
(iii) -10 + 20
(iv) 10 – 20
(v) 7 – (-7)
(vi) -8 – (-10)?
Ans: (i) -5 + 0
Adding 0 to any number does not change the value of the number.
-5 + 0 = -5
(ii) 7 + (-7)
Adding a number to its negative counterpart results in 0.
7 + (-7) = 0
(iii) -10 + 20
To add numbers with different signs, subtract the smaller absolute value from the larger absolute value and take the sign from the larger absolute value.
-10 + 20 = 10
(iv) 10 – 20
Subtracting a larger number from a smaller number gives a negative result.
10 – 20 = -10
(v) 7 – (-7)
Subtracting a negative number is the same as adding the positive counterpart of the number.
7 – (-7) = 7 + 7 = 14
(vi) -8 – (-10)
Subtracting a negative number is the same as adding the positive counterpart of the number.
-8 – (-10) = -8 + 10 = 2
`Page 255
Using the Unmarked Number Line to Add and Subtract
Use unmarked number lines to evaluate these expressions: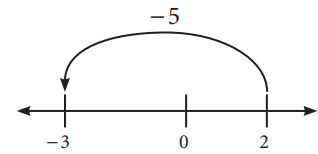
(a) -125 + (-30) = _________
(b) +105 – (-55) = _________
(c) +80 – (-150) = _________
(d) -99 – (-200) = _________
Ans: (a) -125 + (-30)
Adding two negative numbers on the number line ∴ -125 + (-30) = – 125 – 30 = -155
∴ -125 + (-30) = – 125 – 30 = -155
(b) +105 – (-55)
Subtracting a negative number is the same as adding the positive counterpart. ∴ +105 – (-55) = 105 + 55 = 160
∴ +105 – (-55) = 105 + 55 = 160
(c) +80 – (-150)
Subtracting a negative number is the same as adding the positive counterpart. ∴ +80 – (-150) = 80 + 150 = 230
∴ +80 – (-150) = 80 + 150 = 230
(d) -99 – (-200)
Subtracting a negative number is the same as adding the positive counterpart.
∴ -99 – (-200) = -99 + 200 = 101
Page 257
Figure it Out
Q1: Complete the additions using tokens.
a. (+6) + (+4)
Ans: (+6) + (+4)
To represent (+6), we use 6 positive tokens and to represent (+4), we use 4 positive tokens
and to represent (+4), we use 4 positive tokens
 Hence, by combining them, we get
Hence, by combining them, we get ⇒ (+6) + (+4) = (+10)
⇒ (+6) + (+4) = (+10)
∴ Counting all the positive tokens, we get (+10).
b. (-3) + (-2)
Ans: (-3) + (-2)
To represent (-3), we use 3 negative tokens To represent (-2), we use 2 negative tokens
To represent (-2), we use 2 negative tokens Combining them, we get
Combining them, we get ⇒ (-3) + (-2) = -5
⇒ (-3) + (-2) = -5
∴ Counting all the negative tokens, we get (-5).
c. (+5) + (-7)
Ans: (+5) + (-7)
To represent (+5), we use 5 positive tokens
To represent (-7), we use 7 negative tokens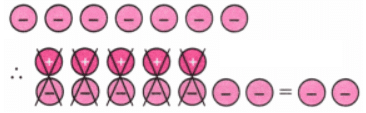 ∴ Remaining tokens = (+5) + (-7) = -2
∴ Remaining tokens = (+5) + (-7) = -2
d. (-2) + (+6)
Ans: (-2) + (+6)
To represent (-2), we use 2 negative tokens To represent (+6), we use 6 positive tokens
To represent (+6), we use 6 positive tokens
Hence,
(-2) + (+6) = +4
Counting the remaining tokens, we get (+4) tokens
(+4) tokens
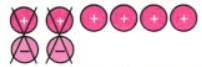
Q2: Cancel the zero pairs in the following two sets of tokens. On what floor is the lift attendant in each case? What is the corresponding addition statement in each case?
Ans: a. From the picture we see that we can remove three pairs.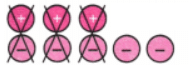
This cancels out to 0.
Remaining tokens =
Since two negative tokens is remaining, the lift attendant is on the second floor below the ground floor.
The corresponding addition statement is (+3) + (-5) = (-2)
b. From the picture we see that we can remove three pairs.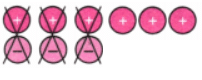 This cancels out to 0.
This cancels out to 0.
Remaining tokens = 
Since three positive tokens are remaining, the lift attendant is on the third floor above the ground floor.
The corresponding addition statement is (+6) + (-3) = (+3)
Page 258
Figure it Out
Q1: Evaluate the following differences using tokens. Check that you get the same result as with other methods you now know:
a. (+10) – (+7)
Ans: Here, from 10 positives take away 7 positives. Hence, (+10) – (+7) = +3
Hence, (+10) – (+7) = +3
b. (-8) – (-4)
Ans: Here, from -8 negatives take away -4 negatives Hence, (-8) – (-4) = -4
Hence, (-8) – (-4) = -4
c. (-9) – (-4)
Ans: Here, from -9 negatives take away -4 negatives. Hence, (-9) – (-4) = -5
Hence, (-9) – (-4) = -5
d. (+9) – (+12)
Ans: There are not enough tokens to take out 12 positives from 9 positives.
So, we put an extra 3 zero pairs (1 pair = a positive and a negative).
Now we can take out 12 positives.

Hence, (+9) – (+12) = -3
e. (-5) – (-7)
Ans: There are not enough tokens to take out -7 negatives from -5 negatives.
So, we put an extra two zero pairs (1 pair = a positive and a negative).
Now we can take out -7 negatives. Hence, (-5) – (-7) = +2
Hence, (-5) – (-7) = +2
f. (-2) – (-6)
Ans: There are not enough tokens to take out -6 negatives from -2 negatives.
So, we put an extra four zero pairs (1 pair = a positive and a negative).
Now we can take out -6 negatives. Hence, (-2) – (-6) = +4
Hence, (-2) – (-6) = +4
Q2: Complete the subtractions:
a. (-5) – (-7)
Ans: There are not enough tokens to take out -7 negatives from -5 negatives.
So, we put an extra two zero pairs (1 pair = a positive and a negative).
Now we can take out -7 negatives. Hence, (-5) – (-7) = +2
Hence, (-5) – (-7) = +2
b. (+10) – (+13)
Ans: There are not enough tokens to take out 13 positives from 10 positives.
So, we put an extra 3 zero pairs (1 pair = a positive and a negative).
Now we can take out 13 positives.

Hence, (+10) – (+13) = -3
c. (-7) – (-9)
Ans: There are not enough tokens to take out -9 negatives from -7 negatives.
So, we put an extra two zero pairs (1 pair = a positive and a negative).
Now we can take out -9 negatives.

Hence, (-7) – (-9) = +2
d. (+3) – (+8)
Ans: There are not enough tokens to take out 8 positives from 3 positives.
So, we put an extra 5 zero pairs (1 pair = a positive and a negative).
Now we can take out 8 positives.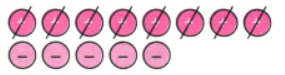 Hence, (+3) – (+8) = -5
Hence, (+3) – (+8) = -5
e. (-2) – (-7)
Ans: There are not enough tokens to take out -7 negatives from -2 negatives.
So, we put an extra two zero pairs (1 pair = a positive and a negative).
Now we can take out -7 negatives. Hence, (-2) – (-7) = +5
Hence, (-2) – (-7) = +5
f. (+3) – (+15)
Ans: There are not enough tokens to take out 15 positives from 3 positives.
So, we put an extra 12 zero pairs (1 pair = a positive and a negative).
Now we can take out 15 positives.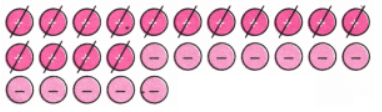 Hence, (+3) – (+15) = -12
Hence, (+3) – (+15) = -12
Page 259
Figure it Out
Q1: Try to subtract: -3 – (+ 5).
How many zero pairs will you have to put in? What is the result?
Ans: We have to take out 5 positives from -3 negatives. But there are not enough positives.
So, we put down an extra 5 zero pairs (1 pair = a positive and a negative).
Now we can take out 5 positives.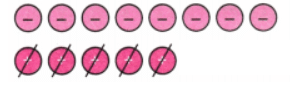 Hence, -3 – (+5) = -8
Hence, -3 – (+5) = -8
Q2: Evaluate the following using tokens.
a. (-3) – (+10)
Ans: (-3) – (+10)
We have to take out 10 positives from -3 negatives. But there are not enough positives.
So, we put down extra 10 zero pairs (1 pair = a positive and a negative).
Now we can take out 10 positives. Hence, (-3) – (+10) = -13
Hence, (-3) – (+10) = -13
b. (+8) – (-7)
Ans: (+8) – (-7)
We have to take out -7 negatives from 8 positives. But there are not enough negatives.
So, we put down an extra 7 zero pairs (1 pair = a positive and a negative).
Now we can take out -7 negatives. Hence, (+8) – (-7) = 15
Hence, (+8) – (-7) = 15
c. (-5) – (+9)
Ans: (-5) – (+9)
We have to take out 9 positives from -5 negatives. But there are not enough positives.
So, we put down an extra 9 zero pairs (1 pair = a positive and a negative).
Now we can take out 9 positives. Hence, -5 – (+9) = -14
Hence, -5 – (+9) = -14
d. (-9) – (+10)
Ans: (-9) – (+10)
We have to take out 10 positives from -9 negatives. But there are not enough positives.
So, we put down an extra 10 zero pairs (1 pair = a positive and a negative).
Now we can take out 10 positives.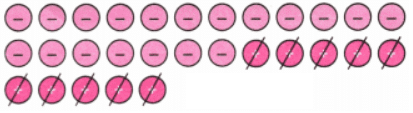 Hence, -9 – (+10) = -19
Hence, -9 – (+10) = -19
e. (+6) – (-4)
Ans: (+6) – (-4)
We have to take out -4 negatives from 6 positives. But there are not enough negatives.
So, we put down an extra 4 zero pairs (1 pair = a positive and a negative).
Now we can take out -4 negatives. Hence, (+6) – (-4) = 10
Hence, (+6) – (-4) = 10
f. (-2) – (+7)
Ans: (-2) – (+7)
We have to take out 7 positives from -2 negatives. But there are not enough positives.
So, we put down an extra 7 zero pairs (1 pair = a positive and a negative).
Now we can take out 7 positives. Hence, (-2) – (+7) = -9
Hence, (-2) – (+7) = -9
Page 260
Figure it Out
Q1: Suppose you start with 0 rupees in your bank account, and then you have credits of ₹ 30, ₹ 40, and ₹ 50, and debits of ₹ 40, ₹ 50, and ₹ 60. What is your bank account balance now?
Ans: Here, Credits = ₹ 30 + ₹ 40 + ₹ 50 = ₹ 120
and Debits = ₹ 40 + ₹ 50 + ₹ 60 = ₹ 150
∴ Balance = Credits – Debits
= ₹ 120 – ₹ 150
= – ₹30
Therefore, your bank account balance is – ₹ 30.
Q2: Suppose you start with 0 rupees in your bank account, and then you have debits of ₹ 1, 2, 4, 8, 16, 32, 64, and 128, and then a single credit of ₹ 256. What is your bank account balance now?
Ans: Here, Debits = ₹ 1 + ₹ 2 + ₹ 4 + ₹ 8 + ₹ 16 + ₹ 32 + ₹ 64 + ₹ 128 = ₹ 255
∴ Balance = Credits – Debits
= ₹ 256 – ₹ 255
= ₹ 1
Therefore, your bank account balance is ₹ 1.
Q3: Why is it generally better to try and maintain a positive balance in your bank account? What are circumstances under which it may be worthwhile to temporarily have a negative balance?
Ans: Having a positive balance in your bank account is generally better because:
- Avoids Overdraft Fees: Many banks charge fees if your account balance goes negative.
- Provide Financial Security: A positive balance ensures you have funds available for unexpected expenses or emergencies.
- Builds Good Credit History: Maintaining a positive balance can help to improve your credit score, making it easier to get loans or credit cards in the future.
There might be a few specific situations where temporarily having a negative balance could be considered:
- Overdraft Protection: Some banks offer overdraft protection which can help avoid bounced checks or declared transactions.
- Planned Large Expenses: If you know you will have a large income soon and need to make essential purchases a temporary negative balance might be acceptable.
Page 261
Figure it Out
Q1: Looking at the geographical cross-section fill in the respective heights: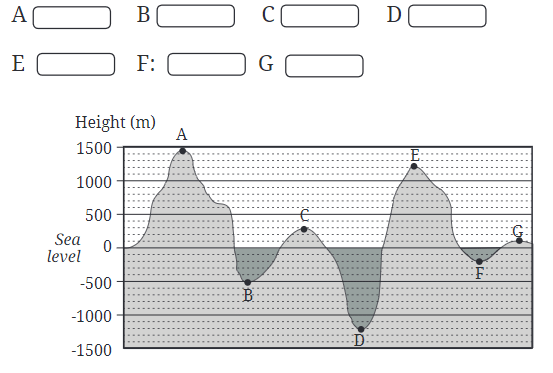 Ans: You will need to estimate the height of each point A to G from the graph.
Ans: You will need to estimate the height of each point A to G from the graph.
Look at the vertical axis to determine the height value corresponding to each point.
Heights:
- A = +1500 m
- B = -500 m
- C = +300 m
- D = -1200 m
- E = +1200 m
- F = -200 m
- G = +100 m
Q2: Which is the highest point in this geographical cross-section? Which is the lowest point?
Ans: Identify the point on the graph that reaches the height point above sea level. Point A shows the highest point. Similarly find the point that is the lowest, considering points below sea level as well. Point D shows the lowest point.
Q3: Can you write the points A, B,……, and G in a sequence of decreasing order of heights? Can you write the points in a sequence of increasing order of heights?
Ans: Based on the heights we determined in question 1, arrange the points from highest to lowest (decreasing order) A > E > C > G > F > B > D and then from lowest to highest (increasing order) D < B < F < G < C < E < A.
Q4: What is the highest point above sea level on Earth? What is its height?
Ans: The highest point on Earth is Mount Everest at a height of 8848 m above sea level.
Q5: What is the lowest point of sea level on land or the ocean floor? What is its height? (This height should be negative).
Ans: The lowest known point on the Earth is Marina Trench, in the Pacific Ocean, at a depth of 11034 m below sea level.
Page 262
Figure it Out
Q1: Do you know that there are some places in India where temperatures can go below 0°C? Find out the places in India where temperatures sometimes go below 0°C. What is common among these places? Why does it become colder there and not in other places? Ans:
Ans:
Places:
- Ladakh: This region is well-known for it’s extremely cold winters, with temperatures often dropping below 0°C.
- Himachal Pradesh: Some high-altitude areas in Himachal Pradesh, especially the northern parts, can experience sub-zero temperatures.
- Jammu & Kashmir: Similar to Ladakh, parts of Jammu and Kashmir, particularly the mountainous regions, face freezing temperatures.
- Sikkim: Being a mountainous state, Sikkim also witness sub-zero temperatures in certain areas.
- Arunachal Pradesh: The higher reaches of Arunachal Pradesh can experience cold conditions with temperatures below 0°C.
Common Factor: All these places are located in the Himalayan region, which is characterized by high altitudes.
Reason for Colder Temperatures:
- High Altitude: As altitude increases, the temperature decreases. This is primarily due to the thinner atmosphere at higher altitudes, which results in less heat retention.
- Distance from the Equator: These regions are farther from the equator receiving less direct sunlight, leading to colder temperatures.
Q2: Left in Ladakh gets very cold during winter. The following is a table of temperature readings taken during different times of the day/night in Leh on a day in November. Match the temperature with the appropriate time of the day/night.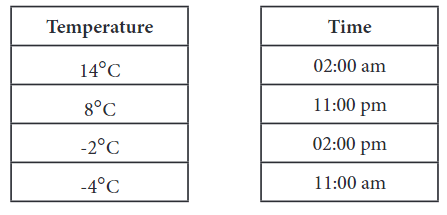 Ans:
Ans: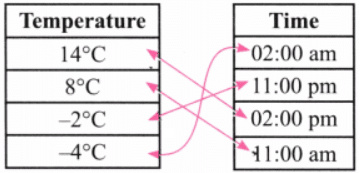
Page 263 & 264
Figure it Out
Q1: Do the calculations for the given grid and find the border sum.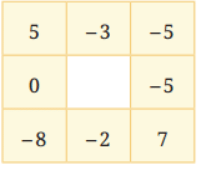 Ans: Let’s analyze the given grid and find the border sum.
Ans: Let’s analyze the given grid and find the border sum.
Understanding the grid.
The given grid is a 3 × 3 arrangement of numbers.
The sum of numbers in each row and column should be the same.
Calculating the Border Sum:
Top row: 5 + (-3) + (-5) = -3
Bottom row: (-8) + (-2) + 7 = -3
Left column: 5 + 0 + (-8) = -3
Right column: (-5) + (-5) + 7 = -3
Therefore, the border sum of the given grid is -3.
Q2: Complete the grids to make the required border sum: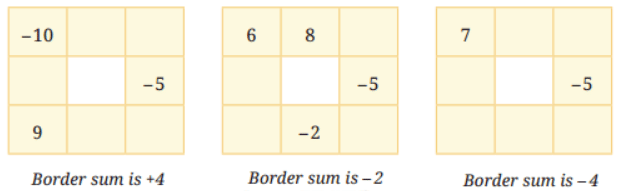 Ans: Here is the completed grid:
Ans: Here is the completed grid: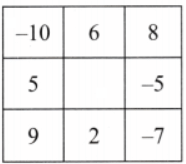 The border sum is +4
The border sum is +4
Explanation: We filled in the missing numbers to ensure the sum of each row and column is equal to the given border sum.
e.g. in the first grid, to get a border sum of +4, the missing number in the top row should be 6 and 8. (Since -10 + 6 + 8 = +4).
Attempt the remaining two grids by yourself.
Q3: For the last grid above, find more than one way of filling the numbers to get the border sum -4.
Ans: There are multiple ways to fill the last grid with a border sum of -4, here are two examples: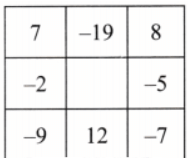
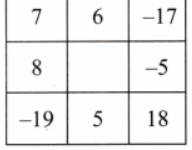
Q4: Which other grids can be filled in multiple ways? What could be the reason?
Ans: Grid with a larger size (more rows and columns) is likely to have multiple solutions. This is because there are more degrees of freedom to distribute numbers while maintaining the border sum.
Q5: Make a border integer square puzzle and challenge your classmates.
Ans: Here’s the puzzle: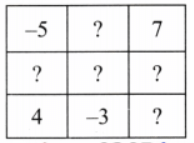
Border sum: 2
[Additional Notes: There might be more than two ways to fill the last grid. Creating larger grids with different order sums can lead to more complex and challenging puzzles.]
Page 265 & 266
Figure it Out
Q1: Try afresh, choose different numbers this time. What sum did you get? Was it different from the first time? Try a few more times!
Ans: Let’s circle the number -5.
Now as per the game, let’s strike out the row and column with the number -5.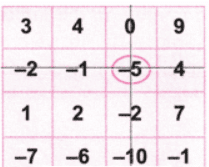 Again let’s circle the number 3.
Again let’s circle the number 3.
Let’s strike out the row and column with the number 3.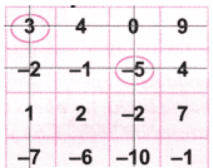 Again let’s circle the number -1.
Again let’s circle the number -1.
Let’s strike out the row and column with the number -1. Again let’s circle the balance number 2.
Again let’s circle the balance number 2.
Let’s strike out the row and column with the number 2. Now let’s add the circled numbers = (-5) + 3 + (-1) + (2) = -6 + 5 = -1
Now let’s add the circled numbers = (-5) + 3 + (-1) + (2) = -6 + 5 = -1
Hence, we get the same value (-1).
Now try yourself.
Q2: Play the same game with the grids below. What answer did you get?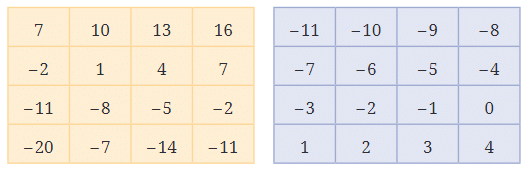 Ans: (a) Let’s circle the number 1.
Ans: (a) Let’s circle the number 1.
Now as per the game, let’s strike out the row and column with number 1.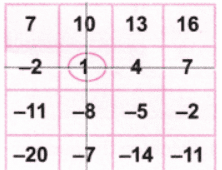 Again let’s circle the number 13.
Again let’s circle the number 13.
Let’s strike out the row and column with the number 13.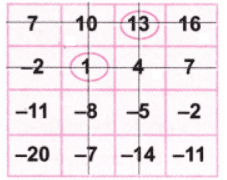 Again let’s circle the number -20.
Again let’s circle the number -20.
Let’s strike out the row and column with the number -20.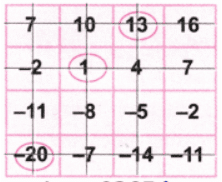 Again let’s circle the balance number 2.
Again let’s circle the balance number 2.
Let’s strike out the row and column with number 2.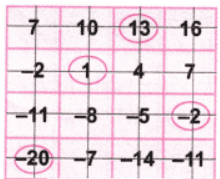 Now let’s add the circled numbers = 1 + 13 – 20 – 2= 14 – 22 = -8 which is the required answer.
Now let’s add the circled numbers = 1 + 13 – 20 – 2= 14 – 22 = -8 which is the required answer.
b. Let’s circle the number 0.
Now as per the game, let’s strike out the row and column with the number 0.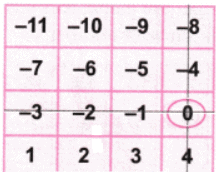 Again let’s circle the number -5.
Again let’s circle the number -5.
Let’s strike out the row and column with the number -5.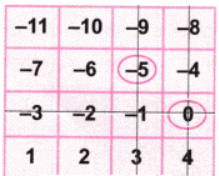 Again let’s circle the number 1.
Again let’s circle the number 1.
Let’s strike out the row and column with the number 1.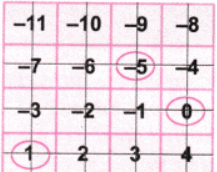 Let’s strike out the row and column with the number -10.
Let’s strike out the row and column with the number -10.
Again let’s circle the balance number -10.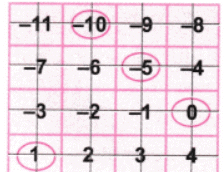 Now let’s add the circled numbers = 0 + (-5) + 1 + (-10) = -14 which is the required answer.
Now let’s add the circled numbers = 0 + (-5) + 1 + (-10) = -14 which is the required answer.
Q3: What could be so special about these grids? Is the magic in the numbers the way they are arranged or both? Can you make more such grids?
Ans: Grids can be fascinating because of both the numbers and the way they are arranged. Here’s why:
- Numbers: The numbers in a grid can follow specific patterns or sequences, such as magic squares where the sums of numbers in each row, column, and diagonal are the same.
- Arrangement: The way elements are arranged in a grid can create visual balance and harmony.
Figure it Out
Q1: Write all the integers between the given pairs, in increasing order.
a. 0 and -7
b. -4 and 4
c. -8 and -15
d. -30 and -23
Ans: a. The integers between 0 and -7, in increasing order, are: -6, -5, -4, -3, -2, -1
b. The integers between -4 and 4, in increasing order, are: -3, -2, -1, 0, 1, 2, 3
c. The integers between -8 and -15, in increasing order, are: -14, -13, -12, -11, -10, -9
d. The integers between -30 and -23, in increasing order, are: -29, -28, -27, -26, -25, -24
Q2: Give three numbers such that their sum is -8.
Ans: Three numbers that add up to -8 are -10, 1, and 3.
When we add them together, we get -10 + 1 + 1 = -8
Q3: There are two dice whose faces have these numbers: -1, 2, -3, 4, -5, 6. The smallest possible sum upon rolling these dice is -10 = (-5) + (-5) and the largest possible sum is 12 = (6) + (6). Some numbers between (-10) and (+12) are not possible to get by adding numbers on these two dice. Find those numbers.
Ans: Let’s find the sums that are not possible when rolling these two dice.
The faces of the dice are: -1, 2, -3, 4, -5, and 6.
First, let’s list all possible sums:
The sum of two negative numbers:
- (-1) + (-1) = -2
- (-1) + (-3) = -4
- (-1) + (-5) = -6
- (-3) + (-3) = -6
- (-3) + (-5) = -8
- (-5) + (-5) = -10
The sum of one negative and one positive number:
- (-1) + 2 = 1
- (-1) + 4 = 3
- (-1) + 6 = 5
- (-3) + 2 = -1
- (-3) + 4 = 1
- (-3) + 6 = 3
- (-5) + 2 = -3
- (-5) + 4 = -1
- (-5) + 6 = 1
The sum of two positive numbers:
- 2 + 2 = 4
- 2 + 4 = 6
- 2 + 6 = 8
- 4 + 4 = 8
- 4 + 6 = 10
- 6 + 6 = 12
Now, let’s list all the possible sums in ascending order:
-10, -8, -6, -4, -3, -2, -1, 1, 3, 4, 5, 6, 8, 10, 12
The sum of numbers between -10 and 12 that are not the sum of possible to get are:
-9, -7, -5, 0, 2, 7, 9, 11
Q4: Solve these:
Ans: (a) 8 – 13 = -5
(b) -8 – (13) = -8 – 13 = -21
(c) -13 – (-8) = -13 + 8 = -5
(d) (-13) + (-8) = -13 – 8 = -21
(e) 8 + (-13) = 8 – 13 = -5
(f) -8 – (-13) = -8 + 13 = 5
(g) (13) – 8 = 13 – 8 = 5
(h) 13 – (-8) = 13 + 8 = 21
Q5: Find the years below.
a. From the present year, which year was it 150 years ago? _______________
Ans: 150 years ago from the present year (2024):
[2024 – 150 = 1874]
So, 150 years ago, it was the year 1874.
b. From the present year, which year was it 2200 years ago? _______________
(Hint: Recall that there was no year 0.)
Ans: 2200 years ago from the present year (2024):
Since there was no year 0, we need to account for this in our calculation:
[2024 – 2200 = -176].
The year -176 corresponds to 177 BCE (Before the Common Era).
So, 2200 years ago, it was the year 177 BCE.
c. What will be the year 320 years after 680 BCE? _______________
Ans: As BCE is before Christ, hence Let’s write 680 BCE = -680
Hence, 320 years after 680 BCE = -680 + 320 = -360 = 360 BCE.
Q6: Complete the following sequences:
a. (-40), (-34), (-28), (-22), _____, ______, ______
Ans: (-40), (-34), (-28), (-22), _____, ______, ______
Let’s subtract a last number of the sequence with the preceding number.
∵ (-22) – (-28) = -22 + 28 = 6
(-28) – (-34) = -28 + 34 = 6
-(34) – (-40) = -34 + 40 = 6
Hence, this is a sequence where each term increases by 6.
∴ Next term = -22 + 6 = -16
∴ Following term = -16 + 6 = -10
∴ Final term = -10 + 6 = -4
Hence, the sequence is (-40), (-34), (-28), (-22), (-16), (-10), (-4)
b. 3, 4, 2, 5, 1, 6, 0, 7, _____, ______, ______
Ans: Let’s subtract the last number of the sequence with the preceding number.
7 – 0 = 7
0 – 6 = -6
6 – 1 = 5
1 – 5 = -4
5 – 2 = 3
2 – 4 = -2
4 – 3 = 1
Hence in this sequence, numbers are decreasing by 1 with alternate positive and negative integers.
Hence the next number
7 + (-8) = -1
-1 + 9 = 8
8 – 10 = -2
-2 + 11 = 9
and so on.
Hence complete sequence is 3, 4, 2, 5, 1, 6, 0, 7, -1, 8, -2, 9,……
Let us check
-1 – 7 = -8
8 + 1 = 9
-2 – 8 = -10
c. _____, ______, 12, 6, 1, (-3), (-6), _____, ______, ______
Ans: _____, ______, 12, 6, 1, (-3), (-6), _____, ______, ______
Let’s subtract the last number of the sequence from the preceding number
(-6) – (-3) = -6 + 3 = -3
(-3) – (1) = -3 – 1 = -4
1 – 6 = -5
6 – 12 = -6
Hence in this sequence, 1 negative integer is added to each number.
Let’s take the first number of the sequence as x and the second number as y.
2nd number = 12 – y = -7
Hence y = 12 + 7 = 19
1st number, let it be x
2nd number 19 – x = -8
⇒ x = 19 + 8 = 27
Now let’s find the 8th number, let it be a.
Hence, a – (-6) = -2
⇒ a = -2 – 6 = -8
Now let’s find the 9th number, let it be b.
Hence b – (-8) = -1
⇒ b = -1 – 8 = -9
Hence, the sequence is: 27, 19, 12, 6, 1, (-3), (-6), (-8), (-9), (-9)
Q7: Here are six integer cards: (+1), (+7), (+18), (-5), (-2), (-9).
You can pick any of these and make an expression using addition(s) and subtraction(s).
Here is an expression: (+18) + (+1) – (+7) – (-2) which gives a value (+14).
Now, pick cards and make an expression such that its value is closer to (-30).
Ans: Let’s try to create an expression that gets as close to (-30) as possible using the given cards: (+1, +7, +18, -5, -2, -9).
One possible expression is: (-9) + (-5) + (-2) + (-18) + (+1)
Let’s calculate the value step by step:
- (-9) + (-5) = -14
- -14 + (-2) = -16
- -16 + (-18) = -34
- -34 + (+1) = -33
Hence, the value of this expression is (-33), which is quite close to (-30).
Q8: The sum of two positive integers is always positive but a (positive integer) – (positive integer) can be positive or negative. What about
a. (Positive) – (Negative)
Ans: (Positive) – (Negative):
Subtracting a negative number is the same as adding its positive counterpart. So, this will always be positive.
For example, 5 – (-3) = 5 + 3 = 8.
b. (Positive) + (Negative)
Ans: (Positive) + (Negative):
This depends on the magnitudes of the numbers. If the positive number is larger, the result is positive; if the negative number is larger, the result is negative.
For example,
7 + (-4) = 3 (positive)
4 + (-7) = -3 (negative)
c. (Negative) + (Negative)
Ans: (Negative) + (Negative):
Adding two negative numbers always results in a negative number.
For example, -2 + (-3) = -5.
d. (Negative) – (Negative)
Ans: (Negative) – (Negative):
This is like adding the positive counterpart of the second number to the first negative number.
If the first negative number is larger in magnitude, the result is negative.
However, if the first negative number is smaller than the second negative number, then it is positive.
For example,
7 + (4) = 3 (positive)
4 + (-7) = -3 (negative)
e. (Negative) – (Positive)
Ans: (Negative) – (Positive):
This will always be negative because you’re subtracting a positive number from a negative number.
For example, -4 – 2 = -6.
f. (Negative) + (Positive)
Ans: (Negative) + (Positive):
Similar to (Positive) + (Negative), it depends on the magnitudes. If the positive number is larger, the result is positive; if the negative number is larger, the result is negative.
For example,
-3 + 5 = 2 (positive)
-5 + 3 = -2 (negative)
Q9: This string has a total of 100 tokens arranged in a particular pattern. What is the value of the string?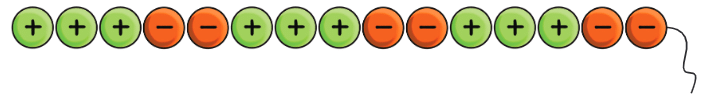 Ans: Let’s analyze the sequence of the string:
Ans: Let’s analyze the sequence of the string:
3, -2, 3, -2, 3, -2 Let’s take a set of 5 tokens as it is repeating, total is 3 – 2 = 1There are 100 tokens in the string.
Let’s take a set of 5 tokens as it is repeating, total is 3 – 2 = 1There are 100 tokens in the string.
Hence total sets = 100/5 = 20 sets
Total of 1 set = 1
Hence, the value of the string = 1 × 20 = 20.
Page 268
Figure it Out
Q1: Can you explain each of Brahmagupta’s rules in terms of Bela’s Building of Fun, or in terms of a number line?
Ans: Let’s break down Brahmagupta’s rules using the concept of Bela’s Building of Fun and a number line. Brahmagupta’s rules primarily deal with operations involving positive and negative numbers. Here’s how we can understand them:
Brahmagupta’s Rules
1. Addition of Positive Numbers:
- Rule: Adding two positive numbers results in a positive number.
- Bela’s Building: If Bela starts on the 3rd floor and moves up 2 floors, she ends up on the 5th floor.
- Number Line: On a number line, moving from 3 to 5 by adding 2.
- Example: (3 + 2 = 5)
2. Addition of Negative Numbers:
- Rule: Adding two negative numbers results in a negative number.
- Bela’s Building: If Bela starts 3 floors below ground level (-3) and moves down 2 more floors, she ends up 5 floors below ground (-5).
- Number Line: Moving from -3 to -5 by adding -2.
- Example: (-3 + (-2) = -5)
3. Addition of a Positive and a Negative Number:
- Rule: Subtract the smaller absolute value from the larger absolute value and keep the sign of the larger absolute value.
- Bela’s Building: If Bela starts on the 3rd floor and moves down 5 floors, she ends up 2 floors below ground (-2).
- Number Line: Moving from 3 to -2 by adding -5.
- Example: (3 + (-5) = -2)
4. Subtraction of a Positive Number from a Negative Number:
- Rule: Subtracting a positive number from a negative number is like adding the two numbers and keeping the negative sign.
- Bela’s Building: If Bela is 3 floors below ground (-3) and moves down 2 more floors, she ends up 5 floors below ground (-5).
- Number Line: Moving from -3 to -5 by subtracting 2.
- Example: (-3 – 2 = -5)
5. Subtraction of a Negative Number from a Positive Number:
- Rule: Subtracting a negative number from a positive number is like adding two numbers.
- Bela’s Building: If Bela starts on the 3rd floor and moves up 2 floors, she ends up on the 5th floor.
- Number Line: Moving from 3 to 5 by subtracting -2.
- Example: (3 – (-2) = 5)
6. Subtraction of a Negative Number from a Negative Number:
- Rule: Subtracting a negative number from another negative number is like adding the absolute values and keeping the negative sign.
- Bela’s Building: If Bela is 3 floors below ground (-3) and moves up 2 floors, she ends up 1 floor below ground (-1).
- Number Line: Moving from -3 to -1 by subtracting -2.
- Example: (-3 – (-2) = -1)
Q2: Give your examples of each rule.
Ans:
1. Addition of Positive Numbers:
- Example: (7 + 4 = 11)
- Bela’s Building: Starting on the 7th floor and moving up 4 floors to the 11th floor.
2. Addition of Negative Numbers:
- Example: (-6 + (-3) = -9)
- Bela’s Building: Starting 6 floors below ground and moving down 3 more floors to 9 floors below ground.
3. Addition of a Positive and a Negative Number:
- Example: (8 + (-5) = 3)
- Bela’s Building: Starting on the 8th floor and moving down 5 floors to the 3rd floor.
4. Subtraction of a Positive Number from a Negative Number:
- Example: (-4 – 3 = -7)
- Bela’s Building: Starting 4 floors below ground and moving down 3 more floors to 7 floors below ground.
5. Subtraction of a Negative Number from a Positive Number:
- Example: (5 – (-2) = 7)
- Bela’s Building: Starting on the 5th floor and moving up 2 floors to the 7th floor.
6. Subtraction of a Negative Number from a Negative Number:
- Example: (-5 – (-3) = -2)
- Bela’s Building: Starting 5 floors below ground and moving up 3 floors to 2 floors below ground.
|
48 videos|334 docs|23 tests
|
FAQs on The Other Side of Zero NCERT Solutions - Mathematics for Class 6
| 1. What is the main theme of "The Other Side of Zero"? |  |
| 2. How does the author explain the importance of zero in mathematics? |  |
| 3. Can you give examples of how zero is used in everyday life? |  |
| 4. What are some common misconceptions about zero addressed in the article? |  |
| 5. How can understanding zero help students in their mathematical studies? |  |






















