Unit Test (Solutions): Number Systems | Mathematics (Maths) Class 9 PDF Download
Time: 1 hour
M.M.: 30
Attempt all questions.
Question numbers 1 to 5 carry 1 mark each.
Question numbers 6 to 8 carry 2 marks each.
Question numbers 9 to 11 carry 3 marks each.
Question numbers 12 & 13 carry 5 marks each.
Q1: What is the product of a rational and an irrational number? (1 Mark)
(i) Always an integer
(ii)Always a rational number
(iii) Always an irrational number
(iv)Sometimes rational and sometimes irrational
Ans:(iii)
The product of a rational and an irrational number is always an irrational number. For example, 2 is a rational number and √3 is irrational. Thus, 2√3 is always an irrational number.
Q2: What is the value of (256)0.16 X (256)0.09? (1 Mark)
(i)4
(ii)16
(iii)64
(iv)256.25
Ans: (i)
(256)0.16 x (256)0.09 = (256)(0.16 + 0.09)
= (256)0.25
= (256)(25/100)
= (256)(1/4)
= (44)(1/4)
= 44(1/4)
= 4
Q3: Add 2√2+ 5√3 and √2 – 3√3. (1 Mark)
Ans:
(2√2 + 5√3) + (√2 – 3√3)
= 2√2 + 5√3 + √2 – 3√3
= (2 + 1)√2 + (5 – 3)√3
= 3√2 + 2√3
Q4: Simplify: (√3+√7) (√3-√7). (1 Mark)
Solution:
(√3 + √7)(√3 – √7)
Using the identity (a + b)(a – b) = a2 – b2,
(√3 + √7)(√3 – √7) = (√3)2 – (√7)2
= 3 – 7
= -4
Q5: Are the square roots of all positive integers irrational? If not, give an example of the square root of a number that is a rational number. (1 Mark)
Ans: No, since the square root of a positive integer 16 is equal to 4. Here, 4 is a rational number.
Q6: Find five rational numbers between 3/5 and 4/5. (2 Marks)
Ans:
We have to find five rational numbers between 3/5 and 4/5.
So, let us write the given numbers by multiplying with 6/6, (here 6 = 5 + 1)
Now,
3/5 = (3/5) × (6/6) = 18/30
4/5 = (4/5) × (6/6) = 24/30
Thus, the required five rational numbers will be: 19/30, 20/30, 21/30, 22/30, 23/30
Q7: Rationalise the denominator of 1/[7+3√3]. (2 Marks)
Ans:
1/(7 + 3√3)
By rationalizing the denominator,
= [1/(7 + 3√3)] [(7 – 3√3)/(7 – 3√3)]
= (7 – 3√3)/[(7)2 – (3√3)2]
= (7 – 3√3)/(49 – 27)
= (7 – 3√3)/22
Q.8: Simplify: (2 Marks)
(i) 72/3.71/5
(ii) 101/2/101/4
Ans:
(i) 72/3.71/5
Bases are equal, so add the powers.
7(2/3 + 1/5)
= 7(10 + 3)/15
= 713/15
(ii) 101/2/101/4
Bases are equal, so subtract the powers.
= 10 (1/2 – 1/4)
= 101/4
Q9: Find three different irrational numbers between the rational numbers 5/7 and 9/11. (3 Marks)
Ans:
The given two rational numbers are 5/7 and 9/11.
5/7 = 0.714285714…..
9/11 = 0.81818181……
Hence, the three irrational numbers between 5/7 and 9/11 can be:
0.720720072000…
0.730730073000…
0.808008000…
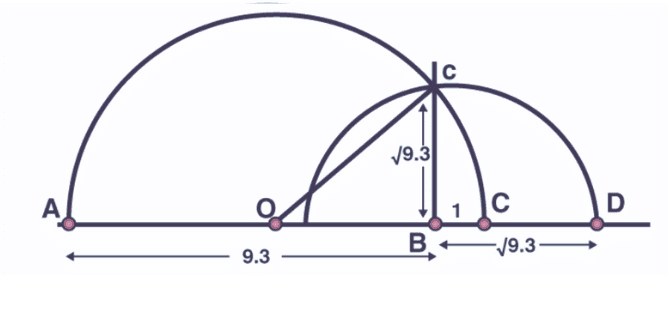
Q.10: Represent √(9.3) on the number line. (3 Marks)
Ans:
Representation of √9.3 on the number line is given below:
Q11: Locate √3 on the number line. (3 Marks)
Ans:
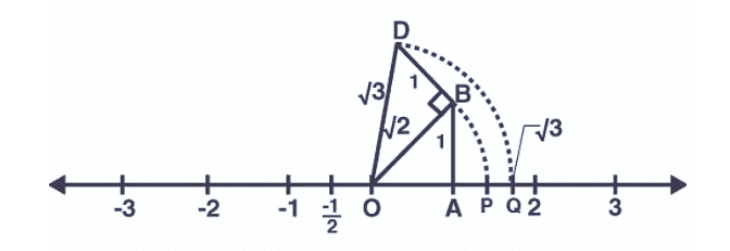
Construct BD of unit length perpendicular to OB (here, OA = AB = 1 unit) as shown in the figure.
By Pythagoras theorem,
OD = √(2 + 1) = √3
Taking O as the centre and OD as radius, draw an arc which intersects the number line at the point Q using a compass.
Therefore, Q corresponds to the value of √3 on the number line.
Q12: Find the decimal expansions of 10/3, 7/8 and 1/7. (5 Marks)
Ans:
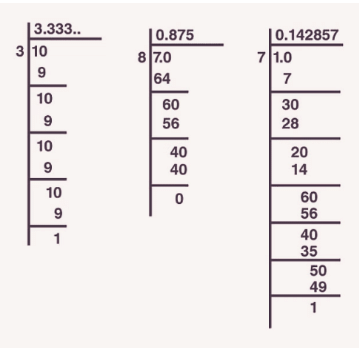
Therefore, 10/3 = 3.3333…
7/8 = 0.875
1/7 = 0.1428571…
Let x = 0.3333….
Multiply with 10,
10x = 3.3333…
Now, 3.3333… = 3 + x (as we assumed x = 0.3333…)
Thus, 10x = 3 + x
10x – x = 3
9x = 3
x = 1/3
Therefore, 0.3333… = 1/3. Here, 1/3 is in the form of p/q and q ≠ 0.
Q13: What can the maximum number of digits be in the repeating block of digits in the decimal expansion of 1/17? Perform the division to check your answer. (5 Marks)
Ans:

Thus, 1/17 = 0.0588235294117647….
Therefore, 1/17 has 16 digits in the repeating block of digits in the decimal expansion.
|
40 videos|471 docs|57 tests
|
FAQs on Unit Test (Solutions): Number Systems - Mathematics (Maths) Class 9
| 1. What are the different types of number systems used in mathematics? |  |
| 2. How do you convert a number from binary to decimal? |  |
| 3. What is the significance of hexadecimal in computer science? |  |
| 4. How do you perform arithmetic operations in different number systems? |  |
| 5. What are some real-life applications of different number systems? |  |

















