Unit Test (Solutions): Patterns in Mathematics | Mathematics for Class 6 PDF Download
Time: 1 hour
Maximum Marks: 30
Attempt all questions.
Question numbers 1 to 5 carry 1 mark each.
Question numbers 6 to 8 carry 2 marks each.
Question numbers 9 to 11 carry 3 marks each.
Question number 12 & 13 carry 5 marks each.
Q1: What is the next number in the sequence: 1, 4, 9, 16, 25? (1 Mark)
Ans: 36
Each number in the sequence is the square of its position in the sequence (1², 2², 3², etc.), so the next number is 6² = 36.
Q2: Find the sum of the first 10 triangular numbers. (1 Mark)
Ans: 220
Triangular numbers are formed by the formula n(n+1)/2. Adding the first 10 gives 1 + 3 + 6 + 10 + 15 + 21 + 28 + 36 + 45 + 55 = 220.
Q3: If you add up the first 6 odd numbers, what square number do you get? (1 Mark)
Ans: 36
The sum of the first 6 odd numbers (1, 3, 5, 7, 9, 11) is 36, which is a square number (6^2).
Q4: Continue the pattern for the next three terms: 1, 2, 4, 8, ___ , ___ , ___. (1 Mark)
Ans: 16, 32, 64
Each term is double the previous term, thus continuing: 8 x 2 = 16, 16 x 2 = 32, 32 x 2 = 64.
Q5: Which of the following is not a sequence of powers? (1 Mark)
(i) 1, 2, 4, 8, 16
(ii) 1, 3, 9, 27, 81
(iii) 1, 5, 25, 125, 625
(iv) 1, 3, 6, 10, 15
Ans: (iv) 1, 3, 6, 10, 15
This sequence represents triangular numbers, not powers, where each term represents a triangular shape formed by dots.
Q6: Visualise the square number 64. (2 Marks)
Ans: 64 can be written as 8 × 8. Thus, it can be shown by dots as:

Q7: Visualize cube number 1000. (2 Marks)
Ans: 1000 can be writen as 10 × 10 × 10. Thus,
 Q8:What is hexagonal number? Represent it pictorially. (2 Marks)
Q8:What is hexagonal number? Represent it pictorially. (2 Marks)
Ans: The numbers that can represent by a hexagon with a dot in the centre and all other dots surrounding the centre dot in a hexagonal shape.
For example: 1, 7, 19, 37, 61, 91, ……
Pictorial representation:


Q9: Complete the following number sequences:(3 Marks)
(a) 1 + 3 + 5 + ___ + 9 + 11 = ____.
(b) 1 + ___ + 3 + 4 + 3 + 2 + 1 = ____.
(c) 1 + 2 + 3 + __ + 5 + __ + 7 +…..+ 11 + __+ …. + 7 + ___ + 5 + 4 + 3 + 2 + 1 = 121
Ans:
(a) 1 + 3 + 5 + 7 + 9 + 11 = 36.
(b) 1 + 2 + 3 + 4 + 3 + 2 + 1 = 16.
(c) 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 10 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 121
Q10: Identify the patterns and write the next three numbers to complete the given patterns.(3 Marks)
(a) 1, 3, 6, 10, 15, ….., …., ….
(b) 1, 4, 9, 16, 25, …, …, ….
(c) 1, 8, 27, 64, 125, …, …, ….
Ans:
(a) The given pattern is as follows:
1, 1 + 2 = 3, 1 + 2 + 3 = 6, 1 + 2 + 3 + 4 = 10, 1 + 2 + 3 + 4 + 5 = 15; a pattern of triangular numbers.
Therefore, the next three numbers of this pattern are:
1 + 2 + 3 + 4 + 5 + 6 = 21,
1 + 2 + 3 + 4 + 5 + 6 + 7 = 28,
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36.
(b) The given pattern is as follows:
1 × 1 = 1, 2 × 2 = 4, 3 × 3 = 9, 4 × 4 = 16, 5 × 5 = 25; a pattern of square numbers.
Therefore, the next three numbers of this pattern are: 6 × 6 = 36, 7 × 7 = 49, 8 × 8 = 64.
(c) The given pattern is as follows:
1 × 1 × 1 = 1, 2 × 2 × 2 = 8, 3 × 3 × 3 = 27, 4 × 4 × 4 = 64, 5 × 5 × 5 = 125; a pattern of cubes.
Therefore, the next three numbers of this pattern are: 6 × 6 × 6 = 216, 7 × 7 × 7 = 343, 8 × 8 × 8 = 512.
Q11: (i) Assertion: 15 is both a triangular number and a square number. (3 Marks)
Reason: If dots arrangement of a number is represented in triangle as well as in square, then the number is called both triangular as well as square number or square- triangular number.
In the given question, a statement of Assertion is followed by a statement of Reason. Choose the correct option as:
(a) Both assertion and reason arp true and the reason is the correct explanation of assertion.
(b) Both assertion and reason are true but the reason is not the correct explanation of the assertion.
(c) Assertion is true and the reason is false.
(d) Assertion is false and the reason is true.
Ans: (d) Since 15 dots can be arranged in a triangle, but cannot be arranged in a square. (ii) Given the sequence 1, 3, 6, 10, 15, find the sum of the next two terms.
(ii) Given the sequence 1, 3, 6, 10, 15, find the sum of the next two terms.
Ans: 49 (21 + 28)
Continuing the sequence of triangular numbers:
6(6+1)/2 = 21,
7(7+1)/2 = 28.
The sum is 21 + 28 = 49.
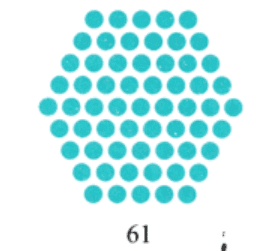
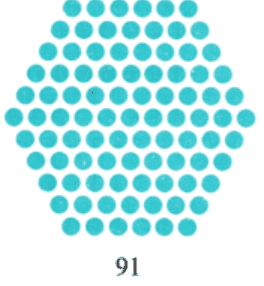
Q12: Represent first 7 centered hexagonal numbers pictorially. (5 Marks)
Ans:
The first six centered hexagonal numbers are as follows: 1, 7, 19, 37, 61, 91, 127.
Pictorial representation: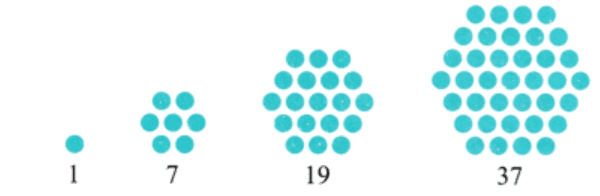

Q13: Case Based Question (5 Marks)
Rima and Diva are playing with square counters.
Rima arranges her counters as follows:

Diva arranges the counters as follows:
 One of their friends, Rohan, says these are showing the number patterns.
One of their friends, Rohan, says these are showing the number patterns.
Based on the above information, answer the following questions.
(a) What are the number patterns they are showing?
(b) If Rima’s arrangement is representing the triangular numbers, then what will be her next two arrangements if she follows the same pattern?
(c) What is Diva’s next arrangement with counters if she follows the same pattern?
Ans:
(a) The number pattern represented by Rima’s arrangement is: 1, 3, 6, …, which are triangular numbers.
Diva’s arrangement represents the pattern: 1,4,9,…, which are square numbers.
(b) The next triangular numbers are 10 and 15. So, Rima’s arrangement for these triangular numbers is as follows: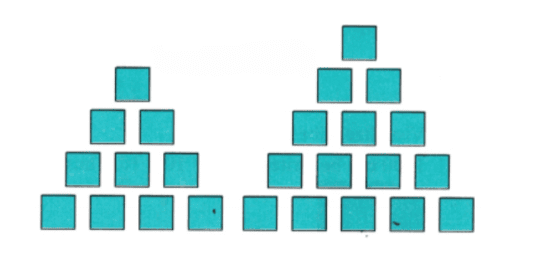 (c) The next square number is 16. So, Diva’s arrangement for the number 16 is as follows:
(c) The next square number is 16. So, Diva’s arrangement for the number 16 is as follows:
|
48 videos|333 docs|23 tests
|
FAQs on Unit Test (Solutions): Patterns in Mathematics - Mathematics for Class 6
| 1. What are some common mathematical patterns found in nature? |  |
| 2. How do hobbies influence mathematical thinking and problem-solving skills? |  |
| 3. What role do patterns play in learning mathematics effectively? |  |
| 4. Can you provide examples of mathematical patterns used in everyday life? |  |
| 5. How can understanding patterns in mathematics benefit students academically? |  |






















