HOTS Questions: How Many Squares? | Mathematics for Class 5: NCERT PDF Download
Q1: Which of these figures represents the area of 12m2 (given that the area of each square = 1 m2)?
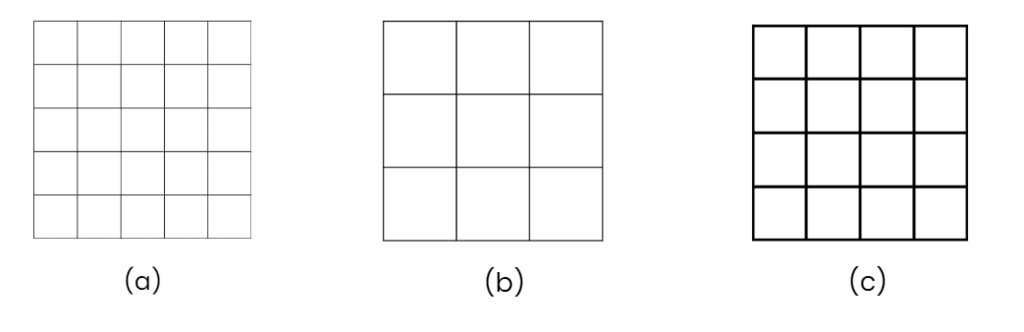 Ans: Figure (c)
Ans: Figure (c)
On counting the squares in each grid, we find that:
Figure (a) has 25 squares, which means its area = 25 m2
Figure (b) has 9 squares, which means its area = 9 m2
Figure (c) has 12 squares, which means its area = 12 m2
Therefore, figure (c) is the answer.
Q2: Given that the side of 1 square = 1 cm in the following figure, find out:
(i) Perimeter
(ii) Area Ans:
Ans:
(i) Perimeter = 16 cm
To find the perimeter, count the sides or edges of the squares that form the boundary of the figure.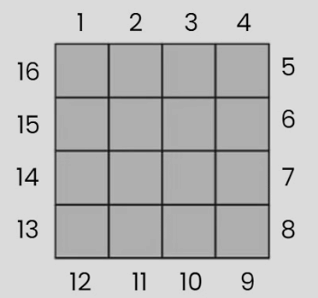
We can see that there are 16 sides/edges of the square that form the boundary of the figure.
(ii) Area = 16 cm2
To find the area of the figure, we can simply count the total number of small squares present in it. This is because area is nothing but space occupied by the shape of the 2D object.
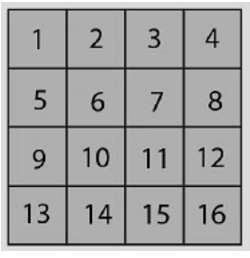
On counting, we find that 16 squares make up the figure, which means that the area of the figure is 16 cm2.
Q3: Which has a bigger area — the screen of a mobile phone or the cover of your favorite book?
Ans: When comparing the area of a mobile screen to the cover of a book, we see that the area of the cover is bigger than that of a mobile screen.
Q4: Write the area in square cm of the shaded portion.
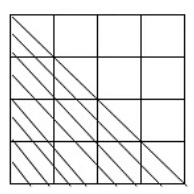
Ans: Total number of squares in the given figure = 16
The shaded portion is half of the given figure.
So the area of the shaded portion = 8 cm2
Q5: Given that the area of the rectangle is 20 square cm, what is the area of the red triangle in the following rectangle?
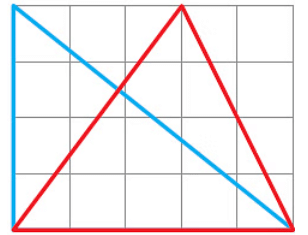 Ans:
Ans:
It can be seen that the red triangle is half of two different rectangles in the figure. We need to find half the area of the orange rectangle and half the area of the green rectangle, and then add them to get the area of the triangle.
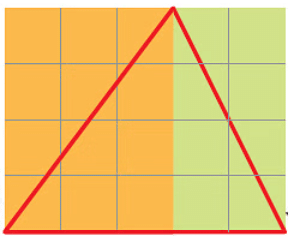
The orange rectangle contains 12 squares
So, the area of the orange rectangle = 12 cm2
Dividing it by half, we get 12/2 = 6 cm2
The green rectangle contains 8 squares
So, the area of the green rectangle = 8 cm2
The area of the green portion of the triangle = 8/2 = 4 cm2
Therefore, the area of the red triangle = 6 + 4 = 10 cm2 or 10 square cm
Q6: Draw one straight line in the following rectangle to divide it into two equal triangles. What is the area of each of the triangles?
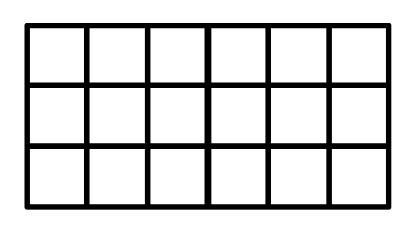
Ans: 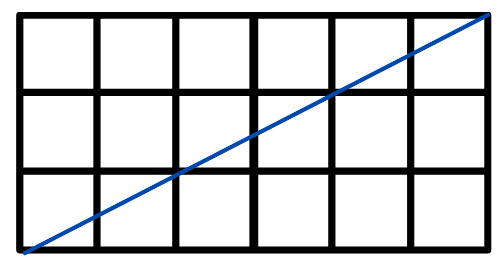
Total number of squares in the figure = 18
Therefore, the area of the rectangle = 18 cm2
Area of each triangles is half the area of the rectangle
So, area of each triangle = 18/2 = 9 cm2
Q7: The perimeter of the following shape is ____. (Side of a square = 1 cm)
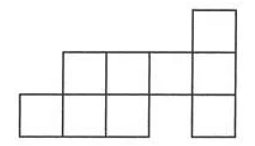 Ans: 18 cm
Ans: 18 cm
The perimeter of the shape can be found out by counting the sides of the squares that form the boundary of the shape.
On counting the sides of the figure, we get 18.
Since a side of a square = 1 cm
Perimeter of the given shape = 18 cm.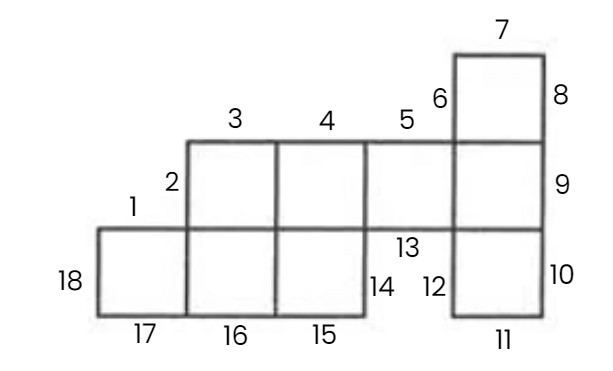
Q8: Look at the figure below and answer the following questions:
(i) Each rectangle is made out of 12 equal squares. Do all rectangles have the same area? Do they have the same perimeter?
(ii) Which of these rectangles has the largest perimeter?
(iii) Which of these rectangles has the smallest perimeter?
Ans:
(i) Since all rectangles are made up of 12 equal squares, they have the same area.
However, they do not have the same perimeter because the boundaries of the rectangles are different.
(ii) From the above figure, we can say that rectangles 1 and 2 have the longest perimeter.
On counting the squares, we see that these rectangles have the perimeter of 26 cm (assuming 1 side of a square = 1 cm).
(iii) From the above figure, we can say that rectangles 3, 4, 5 and 6 have the smallest perimeter.
Each of these have a perimeter of 16 cm.
|
31 videos|192 docs|41 tests
|
FAQs on HOTS Questions: How Many Squares? - Mathematics for Class 5: NCERT
| 1. What is the formula to calculate the number of squares in a grid? |  |
| 2. How do you count squares of different sizes in a grid? |  |
| 3. Can you explain why the number of squares increases as the grid size increases? |  |
| 4. Are there any specific techniques to visually count squares in a complex grid? |  |
| 5. How can understanding the number of squares help in problem-solving in geometry? |  |

























