Mathematics Olympiad Previous Year Papers - 1 | Mathematical Olympiad Class 8 PDF Download
| Table of contents |

|
| Logical Reasoning |

|
| Mathematical Reasoning |

|
| Everyday Mathematics |

|
| Achievers Section |

|
Note:The questions provided in this document are similar to the questions that were asked in the actual Olympiad exam. So, we recommend you study these for your Olympiad preparation
Logical Reasoning
Q1: In a certain code language, ‘SUBJECTS’ is written as ‘UWDLCARQ’, then how will ‘AIRFORCE’ be written in that language?
(a) CKTHQTEG
(b) CKTHMPAC
(c) YGPDMPAC
(d) YKTHMPAC
 View Answer
View Answer 
Ans:(b)
We have,
Comparing the positions of the letters in the alphabet:
- S → U: Move +2 forward.
- U → W: Move +2 forward.
- B → D: Move +2 forward.
- J → L: Move +2 forward.
- E → C: Move -2 backward.
- C → A: Move -2 backward.
- T → R: Move -2 backward.
- S → Q: Move -2 backward.
The positions of the letters alternate:
- First 4 letters → +2 forward in the alphabet.
- Last 4 letters → -2 backward in the alphabet.
Similarly,
Apply the Pattern to "AIRFORCE"
A I R F O R C E
- A → C: Move +2 forward.
- I → K: Move +2 forward.
- R → T: Move +2 forward.
- F → H: Move +2 forward.
- O → M: Move -2 backward.
- R → P: Move -2 backward.
- C → A: Move -2 backward.
- E → C: Move -2 backward.
The coded form of "AIRFORCE" is: CKTHMPAC
Q2: Three figures, X, Y, and Z, show a sequence of folding a piece of paper. Figure Z displays how the folded paper has been cut. Choose a figure from the options that represents the unfolded form of Figure Z.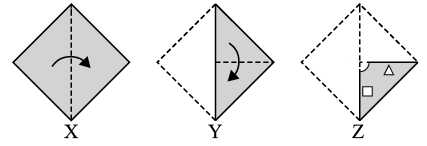
(a)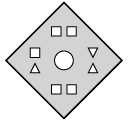 (b)
(b)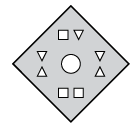
(c)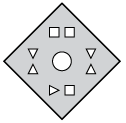
(d)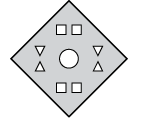
 View Answer
View Answer 
Ans: (d)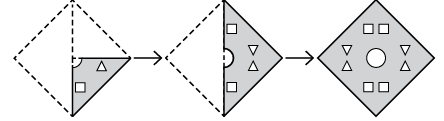
Q3: Which of the following Venn diagrams best represents the relationship between "Fathers, Doctors, and Mothers"?
(a)  (b)
(b)
(c)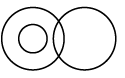 (d)
(d)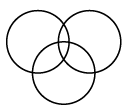
 View Answer
View Answer 
Ans: (a)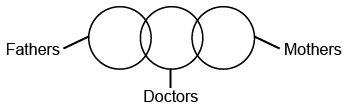
Q4: Which of the following options will continue the given series?
K7J, N14I, Q21H, T28G
(a) W35F
(b) U35D
(c) W34E
(d) U35F
 View Answer
View Answer 
Ans:(a)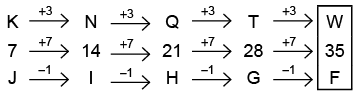
Q5. Find the minimum number of straight lines required to draw the given figure.
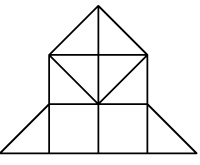 (a) 10
(a) 10
(b) 11
(c) 12
(d) More than 12
 View Answer
View Answer 
Ans:(c)
Minimum number of straight lines required to draw the given figure is 12.
Q6: If the digits in the number 745293 are sorted in ascending order, what will be the difference between the second digit from the right end and the third digit from the left end in this new arrangement?
(a) 3
(b) 4
(c) 2
(d) 1
 View Answer
View Answer 
Ans:(a)
- First, arrange the digits of 745293 in ascending order: 2, 3, 4, 5, 7, 9.
- The second digit from the right in this arrangement is 7.
- The third digit from the left is 4.
- Now, calculate the difference: 7 - 4 = 3.
- Thus, the answer is 3.
Q7: Three positions of a dice are shown below. How many dots are on the face opposite the face with two dots? (a) 3
(a) 3
(b) 5
(c) 4
(d) 1
 View Answer
View Answer 
Ans: (b)
The number of dots on opposite faces are: (1, 4), (2, 5) and (3, 6).
Q8: Examine the information provided and respond to the question below. ‘A * B’ indicates that ‘A is the father of B’. ‘A + B’ signifies that ‘A is the sister of B’. ‘A – B’ denotes that ‘A is the brother of B’. ‘A ÷ B’ implies that ‘A is the mother of B’. What is the relationship of M to N in ‘M + J * L – N’?
(a) Mother
(b) Aunt
(c) Grandmother
(d) Sister
 View Answer
View Answer 
Ans: (b)
- First, we break down the expression ‘M + J * L – N’ step by step.
- ‘M + J’ means M is the sister of J.
- ‘J * L’ means J is the father of L.
- Now, we know M is the sister of J, and J is the father of L, which makes M the aunt of L.
- Finally, since N is the sibling of L, M is also the aunt of N.
Q9: Select the correct water image of the given figure.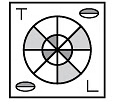 (a)
(a) 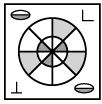 (b)
(b)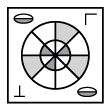 (c)
(c)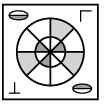 (d)
(d)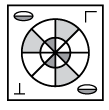
 View Answer
View Answer 
Ans:(b)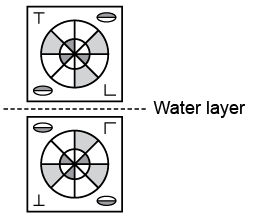
Q10: Vikram left his home and walked 25 m towards the East. He then turned right and walked 40 m, then turned right again and walked 8 m. Finally, he turned right and walked 8 m to reach his school. In which direction is he now with respect to his home?
(a) South
(b) North-West
(c) East
(d)South-East
 View Answer
View Answer 
Ans:(d)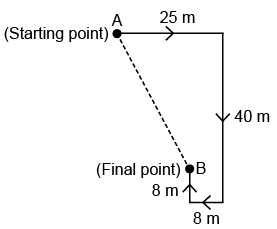
So, Vikram is in South-East direction with respect to his home.
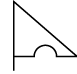
Q11: Select a figure from the options that is exactly embedded in the given figure as one of its parts.
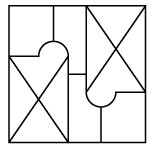
(a)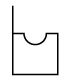 (b)
(b) (c)
(c)  (d)
(d)
 View Answer
View Answer 
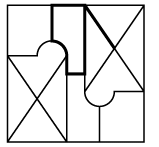
Q12: How many pairs of letters are there in the word "ORIGINAL," each of which has the same number of letters between them as in the English alphabet?
(a) One
(b) Two
(c) Three
(d) More than three
 View Answer
View Answer 
Ans: (d)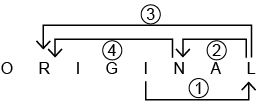
Q13: Which of the following changes in operations would validate the given equation? 18 + 12 × 2 ÷ 5 – 20 = 28
(a) + and ÷
(b) ÷ and ×
(c) + and –
(d) ÷ and –
 View Answer
View Answer 
Ans:(b)
- To determine which operations to switch, we need to analyze the equation: 18 + 12 × 2 ÷ 5 – 20 = 28.
- By changing ÷ and ×, we can recalculate the left side: 18 + 12 ÷ 2 × 5 – 20.
- This results in 18 + 6 × 5 – 20, which simplifies to 18 + 30 – 20 = 28.
- Thus, the correct interchange of operations is ÷ and ×, making the equation true.
Q14: Select a figure from the options that satisfies the same conditions of placement of the dots as in the given figure.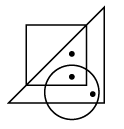 (a)
(a) 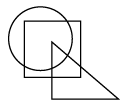 (b)
(b) 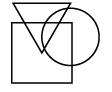 (c)
(c) 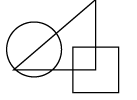
(d)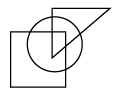
 View Answer
View Answer 
Ans:(b)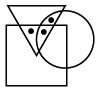
Q15: There is a specific connection between the numbers on both sides of ::. Determine the relationship and find the unknown number.
16 : 51 :: 18 : ?
(a) 57
(b) 54
(c) 61
(d) 60
 View Answer
View Answer 
Ans:(a)
- To find the missing number, we first look at the relationship between 16 and 51.
- The relationship can be seen as: 16 multiplied by 3 plus 3 equals 51 (16 * 3 + 3 = 51).
- Now, applying the same logic to 18: 18 multiplied by 3 plus 3 gives us 57 (18 * 3 + 3 = 57).
- Thus, the missing number is 57, which corresponds to option (a).
Mathematical Reasoning
Q16: If 40% of 1640 plus X equals 35% of 980 plus 150% of 850, what is the value of X?
(a) 715
(b) 962
(c) 844
(d) 648
 View Answer
View Answer 
Ans:(b)
- First, calculate 40% of 1640: 0.4 * 1640 = 656.
- Next, calculate 35% of 980: 0.35 * 980 = 343.
- Then, calculate 150% of 850: 1.5 * 850 = 1275.
- Now, set up the equation: 656 + X = 343 + 1275.
- Simplifying the right side gives: 656 + X = 1618.
- To find X, subtract 656 from 1618: X = 1618 - 656 = 962.
Q17: Factor the expression 25(x + y)² – 36(x – 2y)².
(a) (11x – 7y)(17y – x)
(b) (11x + 7y)(17y + x)
(c) (11x – 7y)(11x – 7y)
(d) (17y – x)(17y – x)
 View Answer
View Answer 
Ans:(a)
- The expression is a difference of squares, which can be factored using the formula a² - b² = (a - b)(a + b).
- Here, let a = 5(x + y) and b = 6(x - 2y). So, we rewrite the expression as (5(x + y) - 6(x - 2y))(5(x + y) + 6(x - 2y)).
- After simplifying, we find the factors to be (11x - 7y) and (17y - x).
- Thus, the correct factorization is (11x – 7y)(17y – x).
Q18: The following figure represents a: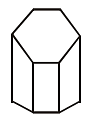 (a) Polygon
(a) Polygon
(b) Convex polyhedron
(c) Cylinder
(d) None of these
 View Answer
View Answer 
Ans: (b)
Convex polyhedron, as it is bounded by plane polygonal faces.
Q19: Solve for x: x - [3x - (2x - 5/10)] = 1/6 (2x - 57) - 5/3
(a) 19
(b) 7
(c) –10
(d) 5
 View Answer
View Answer 
Ans:(d)
- First, simplify the left side: x - [3x - (2x - 0.5)] = x - [3x - 2x + 0.5] = x - [x + 0.5] = -0.5.
- Now, simplify the right side: 1/6 (2x - 57) - 5/3 = (2x - 57)/6 - 5/3 = (2x - 57)/6 - 10/6 = (2x - 67)/6.
- Set the two sides equal: -0.5 = (2x - 67)/6.
- Multiply both sides by 6: -3 = 2x - 67, leading to 2x = 64, so x = 32.
Q20: A number is multiplied by 2/3 of itself and then 61 is taken away from the resulting product. If the end result is 9200, what is the number?
(a) 36
(b) 63
(c) 67
(d) 37
 View Answer
View Answer 
Ans:(b)
- Let the number be represented as x.
- The expression for the operation is (2/3)x * x - 61 = 9200.
- This simplifies to (2/3)x^2 - 61 = 9200.
- Adding 61 to both sides gives (2/3)x^2 = 9261.
- Multiplying both sides by (3/2) results in x^2 = 13891.5.
- Taking the square root gives x ≈ 63, which is the correct answer.
Q21: At what annual simple interest rate does the interest on `1200 over 2 years match the interest on `600 over 4 years at a rate of 7/2% per annum?
(a) 7/2%
(b) 3/5%
(c) 7/8%
(d) None of these
 View Answer
View Answer 
Ans: (a)
- To find the interest on `600 for 4 years at 7/2%, we use the formula: Interest = Principal × Rate × Time.
- Calculating this gives: Interest = 600 × (7/2)/100 × 4 = 84.
- Now, for `1200 over 2 years, we set up the equation: 1200 × Rate × 2 = 84.
- Solving for Rate gives us Rate = 84 / (1200 × 2) = 0.035 or 3.5%, which is equal to 7/2%.
Q22: The smallest number by which 136 must be multiplied so that it becomes a perfect square is
(a) 2
(b) 17
(c) 34
(d) None of these
 View Answer
View Answer 
Ans:(c)
Resolve 136 into prime factors and make group of two of each prime factor
136 = 2 x 2 x 2 x 17 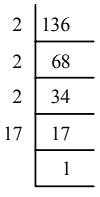 136 = (2 × 2) × 2 × 17We find that 2 and 17 doesn't appear in group of two. So, 136 has to be multiplied with 34 to make it a perfect square.∴ 136 × 2 × 17 = (2 × 2) × (2 × 2) × (17 × 17)
136 = (2 × 2) × 2 × 17We find that 2 and 17 doesn't appear in group of two. So, 136 has to be multiplied with 34 to make it a perfect square.∴ 136 × 2 × 17 = (2 × 2) × (2 × 2) × (17 × 17)
⇒ 4624 = (2 × 2) × (2 × 2) × (17 × 17)
⇒ Required square root = 2 × 2 × 17 = 68
Q23: What needs to be added to 3/8 - (-2/7) in order to obtain 5/14?
(a) 37/56
(b) –27/14
(c) –37/56
(d) –17/56
 View Answer
View Answer 
Ans: (d)
- First, calculate 3/8 - (-2/7). This is the same as 3/8 + 2/7.
- To add these fractions, find a common denominator, which is 56. Convert both fractions: 3/8 becomes 21/56 and 2/7 becomes 16/56.
- Now, add them: 21/56 + 16/56 = 37/56.
- Next, set up the equation: 37/56 + x = 5/14. Convert 5/14 to a fraction with a denominator of 56, which is 20/56.
- Now, solve for x: x = 20/56 - 37/56 = -17/56.
Q24: The scale on a map is 1 mm : 4m. Find the distance on the map for an actual distance of 52 m.
(a) 14 m
(b) 52 mm
(c) 13 mm
(d) 6 mm
 View Answer
View Answer 
Ans: (c)
Distance on map for an actual distance of 4 m = 1 mm.
Distance on map for actual distance of 52 m =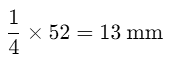
Thus, distance on map for actual distance of 52 m is 13 mm.
Q25: Determine the ratio of the marks obtained by Ashima in Mathematics during Test I and Test III combined to the marks she received in Science during Test II and Test IV combined.
(a) 14:15
(b) 15:14
(c) 15:17
(d) 17:14
 View Answer
View Answer 
Ans:(d)
- To find the ratio, first, add the marks Ashima scored in Mathematics for Test I and Test III.
- Next, add the marks she scored in Science for Test II and Test IV.
- Finally, divide the total marks in Mathematics by the total marks in Science to get the ratio.
- The resulting ratio simplifies to 17:14, which is the correct answer.
Q26: Which of the following statements is accurate?
(a) When two integers are added in any order, then the sum always remains the same.
(b) On a number line, the value of (–71 + 52) lies to the left of (71 – 52).
(c) If p and q are positive integers such that p is prime and q is composite, then pq cannot be an even integer.
(d) All of these
 View Answer
View Answer 
Ans:(a)
- When adding integers, the order does not affect the sum. This is known as the commutative property of addition.
- The statement in option (b) is incorrect because (–71 + 52) equals –19, which is indeed to the left of (71 – 52) which equals 19.
- In option (c), if p is a prime number (like 2) and q is a composite number (like 4), then pq can be even (2 * 4 = 8).
- Thus, the only correct statement is option (a).
Q27: If x = (3/2)² x (2/3)⁻⁴, what is the value of x – 2?
(a) (4/3)¹²
(b) (2/3)¹²
(c) (3/2)¹²
(d) (3/4)¹²
 View Answer
View Answer 
Ans:(b)
- First, calculate x: x = (3/2)² x (2/3)⁻⁴.
- Convert (2/3)⁻⁴ to its reciprocal: (2/3)⁻⁴ = (3/2)⁴.
- Now, x becomes: x = (3/2)² x (3/2)⁴ = (3/2)^(2+4) = (3/2)⁶.
- Next, find x – 2: x – 2 = (3/2)⁶ – 2. To express 2 in terms of (3/2), we can rewrite it as (2/3)¹².
- Thus, the value of x – 2 simplifies to (2/3)¹².
Q28: How much is x³ + 3x²y – 3xy² – y³ less than 4x³ – 2x²y + 5xy² – y³?
(a) 3x³ + 6x²y – 8xy²
(b) -3x³ - 5x²y + 8x²y²
(c) 3x³ - 8x²y + 5xy²
(d) 3x³ - 5x²y + 8xy²
 View Answer
View Answer 
Ans:(d)
- To find how much x³ + 3x²y – 3xy² – y³ is less than 4x³ – 2x²y + 5xy² – y³, we subtract the first expression from the second.
- This gives us: (4x³ – 2x²y + 5xy² – y³) - (x³ + 3x²y – 3xy² – y³).
- Simplifying this results in 3x³ - 5x²y + 8xy², which is option (d).
- Thus, the answer is 3x³ - 5x²y + 8xy², indicating how much less the first expression is compared to the second.
Q29: The adjacent figure shows 3 different views of a three-dimensional figure made from cubes. Which could be a drawing of the figure?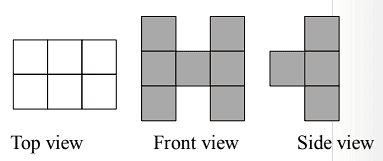 (a)
(a) (b)
(b)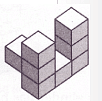
(c) 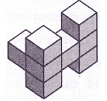
(d) 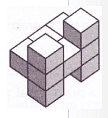
 View Answer
View Answer 
Ans: (d)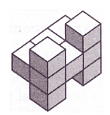
Q30: A square pyramid is shown in the figure. Total number of edges, vertices, and lateral faces are denoted by E, V, and F. The value of F + V – E.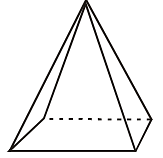 (a) 4
(a) 4
(b) 5
(c) 2
(d) 7
 View Answer
View Answer 
Ans: (c)
A square pyramid has 5 faces, 8 edges, and 5 vertices.
So, 5+5−8=2.
Q31: If m = 3√(140 x 2450) and n = 3√(-216), what is the value of 3√(m + n)?
(a) 6
(b) 8
(c) 4
(d) 64
 View Answer
View Answer 
Ans: (c)
- First, calculate m: m = 3√(140 x 2450). This simplifies to m = 3√(343000) which equals 70.
- Next, calculate n: n = 3√(-216). Since the cube root of a negative number is negative, n = -6.
- Now, find m + n: 70 + (-6) = 64.
- Finally, calculate 3√(64), which equals 4.
Q32: If 1600 increases to 2000 in 2 years at a specific rate of compound interest per annum, what will the total amount be after 4 years?
(a) 3600
(b) 2000
(c) 3500
(d) 2500
 View Answer
View Answer 
Ans:(d)
- To find the total amount after 4 years, we first determine the rate of interest using the formula for compound interest.
- From 1600 to 2000 in 2 years, we can calculate the interest rate. The formula for compound interest is A = P(1 + r)^n, where A is the amount, P is the principal, r is the rate, and n is the number of years.
- Using the values, we find that the rate of interest leads to an amount of 2500 after 4 years, as the interest compounds.
- Thus, the total amount after 4 years is 2500.
Q33: How many sides does a regular polygon possess if each of its interior angles is 120°?
(a) 6
(b) 7
(c) 5
(d) 8
 View Answer
View Answer 
Ans:(a)
- To find the number of sides in a regular polygon, we can use the formula for the interior angle: Interior Angle = (n - 2) * 180° / n, where n is the number of sides.
- Setting the interior angle to 120°, we have: 120 = (n - 2) * 180 / n.
- By solving this equation, we find that n = 6, meaning the polygon has 6 sides.
- Thus, the correct answer is (a) 6, which corresponds to a regular hexagon.
Q34: A die is rolled. What is the probability of rolling a number that is less than or equal to 4?
(a) 4/5
(b) 1/3
(c) 2/3
(d) 1/2
 View Answer
View Answer 
Ans:(c)
- When a die is rolled, it has 6 faces numbered from 1 to 6.
- The numbers that are less than or equal to 4 are 1, 2, 3, and 4. This gives us 4 favorable outcomes.
- The total number of possible outcomes when rolling a die is 6.
- Thus, the probability is calculated as the number of favorable outcomes divided by the total outcomes: 4/6, which simplifies to 2/3.
Q35: Which of the following options indicates that x and y have a direct variation?
(a) (x: 4, 2, 1) (y: 25, 50, 100)
(b) (x: 5, 20, 15) (y: 12, 3, 4)
(c) (x: 7, 21, 42) (y: 28, 84, 168)
(d) Both A and B
 View Answer
View Answer 
Ans:(c)
- To determine if x and y vary directly, we check if the ratio of y to x is constant.
- In option (c), the ratios are: 28/7 = 4, 84/21 = 4, and 168/42 = 4, which are all equal.
- This shows that as x increases, y also increases proportionally, confirming a direct variation.
- Options (a) and (b) do not maintain a constant ratio, hence they do not show direct variation.
Everyday Mathematics
Q36: A man purchases a piece of agricultural land for 300000. He sells one-third of it at a loss of 20% and two-fifths at a profit of 25%. What price should he sell the remaining land for to achieve an overall profit of 10%?
(a) 120000
(b) 100000
(c) 75000
(d) 95000
 View Answer
View Answer 
Ans:(b)
- The total cost of the land is 300000.
- He sells one-third (100000) at a 20% loss, which means he receives 80000 for it.
- He sells two-fifths (120000) at a 25% gain, which means he receives 150000 for it.
- Now, he has sold 220000 in total, and to achieve a 10% profit, he needs to sell the remaining land for 330000 in total.
- This means he must sell the remaining land for 110000. Since he has already sold for 220000, he needs to sell the remaining land for 100000 to reach his goal.
Q37: The size of a red blood cell is 0.000007 m and the size of a plant cell is 0.00001275 m. Find the ratio of the size of red blood cell to that of plant cell.
(a) 13:56
(b) 28:51
(c) 31:39
(d) 22:31
 View Answer
View Answer 
Ans: (b)
- To find the ratio of the size of a red blood cell to that of a plant cell, we divide the size of the red blood cell (0.000007 m) by the size of the plant cell (0.00001275 m).
- This gives us a ratio of 0.000007 m / 0.00001275 m, which simplifies to approximately 0.549.
- When we convert this decimal into a ratio, we find that it is equivalent to 28:51.
- Thus, the correct answer is (b) 28:51, which represents the size comparison between the two types of cells.
Q38: A sum of 3000 is divided between two interest rates: 3% per annum simple interest for 7/2 years and 2% per annum simple interest for 4 years. If the total interest earned amounts to 280, what is the amount lent at 3% per annum?
(a) 1600
(b) 1400
(c) 1800
(d) 2000
 View Answer
View Answer 
Ans:(a)
- Let the amount lent at 3% be x. Then, the amount lent at 2% is 3000 - x.
- The interest from the amount at 3% for 7/2 years is calculated as: Interest = Principal × Rate × Time = x × 3/100 × 7/2.
- The interest from the amount at 2% for 4 years is: Interest = (3000 - x) × 2/100 × 4.
- Setting up the equation: (x × 3/100 × 7/2) + ((3000 - x) × 2/100 × 4) = 280.
- Solving this equation gives x = 1600, which is the amount lent at 3% per annum.
Q39: A train T moving at a speed of 54 km/h passes an electric pole in 20 seconds. Calculate the time it takes to cross a bridge that is 900 meters long (in seconds).
(a) 70
(b) 50
(c) 40
(d) None of these
 View Answer
View Answer 
Ans:(c)
- First, convert the speed of the train from km/h to m/s: 54 km/h = 54 * (1000/3600) = 15 m/s.
- The length of the train can be calculated using the formula: Distance = Speed × Time. Here, Distance = 15 m/s × 20 s = 300 m.
- To cross the bridge, the train needs to cover its own length plus the length of the bridge: 300 m + 900 m = 1200 m.
- Now, calculate the time to cross the bridge: Time = Distance / Speed = 1200 m / 15 m/s = 80 seconds.
Q40: A, B, and C can complete a task in 12, 18, and 9 days, respectively. A began the task and worked for 4 days. After that, B worked alone for 2 days. How many days would C need to finish the remaining work?
(a) 5
(b) 4
(c) 3
(d) 6
 View Answer
View Answer 
Ans: (a)
- First, calculate the work done by A in 4 days. A's rate is 1/12, so in 4 days, A completes 4/12 = 1/3 of the work.
- Next, B works for 2 days. B's rate is 1/18, so in 2 days, B completes 2/18 = 1/9 of the work.
- Now, total work done by A and B is 1/3 + 1/9. To add these, find a common denominator (which is 9): 1/3 = 3/9, so 3/9 + 1/9 = 4/9.
- The remaining work is 1 - 4/9 = 5/9. C's rate is 1/9, so to find out how long C takes to finish 5/9 of the work, use the formula: time = work/rate = (5/9) / (1/9) = 5 days.
Q41: A reservoir is shaped like a cuboid with dimensions of length 8 m, breadth 6 m, and height 3 m. Water enters the reservoir through a pipe at a rate of 60 liters per minute. Calculate the time required for the pipe to completely fill the reservoir.
(a) 30 hrs
(b) 24 hrs
(c) 40 hrs
(d) 52 hrs
 View Answer
View Answer 
Ans: (c)
- First, calculate the volume of the reservoir: Volume = length × breadth × height = 8 m × 6 m × 3 m = 144 m³.
- Convert the volume from cubic meters to liters: 1 m³ = 1000 liters, so 144 m³ = 144,000 liters.
- Next, determine the time taken to fill the reservoir: Time = Total volume / Rate of flow = 144,000 liters / 60 liters/min = 2400 minutes.
- Convert minutes to hours: 2400 minutes ÷ 60 = 40 hours.
Q42: In a school with 30 teachers, one teacher aged 60 years has retired. A new teacher aged 30 years has been hired to take his place. What will happen to the average age of the teachers?
(a) Decrease by 6 months
(b) Remain same
(c) Decrease by 1 year
(d) Decrease by 2 years
 View Answer
View Answer 
Ans: (c)
- The average age of the teachers is calculated based on the total age of all teachers divided by the number of teachers.
- When the 60-year-old teacher retires, the total age decreases significantly, while the 30-year-old teacher's age is much lower.
- This change results in a net decrease in the total age of the teachers, leading to a decrease in average age.
- Specifically, the average age will decrease by 1 year due to this replacement.
Q43: Four years back, Shyam was 3/4 the age of Ram. In four years, Shyam will be 5/6 the age of Ram. What is Shyam's current age?
(a) 20 years
(b) 24 years
(c) 16 years
(d) 30 years
 View Answer
View Answer 
Ans: (c)
- Let Shyam's current age be S and Ram's current age be R.
- Four years ago, Shyam's age was S - 4 and Ram's age was R - 4. The equation is: S - 4 = (3/4)(R - 4).
- In four years, Shyam's age will be S + 4 and Ram's age will be R + 4. The equation is: S + 4 = (5/6)(R + 4).
- Solving these two equations gives S = 16, which means Shyam is currently 16 years old.
Q44: There are three poles, A, B, and C. The height of pole C is two-thirds of pole B, and the height of pole B is four-thirds of pole A. Determine the height of pole C, given that the height of pole A is 97/3 m.
(a) 15 10/63 m
(b) 3 17/27 m
(c) 28 20/27 m
(d) 4 20/63 m
 View Answer
View Answer 
Ans:(c)
- First, calculate the height of pole B using the height of pole A: height of B = (4/3) * (97/3) = 388/9 m.
- Next, find the height of pole C: height of C = (2/3) * (388/9) = 776/27 m.
- Convert 776/27 m to a mixed number: 776 ÷ 27 = 28 with a remainder of 20, so height of C = 28 20/27 m.
- Thus, the height of pole C is 28 20/27 m.
Q45: Atul is in a playground shaped like a parallelogram. He notices that the lengths of the diagonals are 80 m and 60 m. Therefore, the playground could be shaped like ______.
(a) Rectangle
(b) Rhombus
(c) Kite
(d) Square
 View Answer
View Answer 
Ans: (b)
- The playground is a parallelogram, which means opposite sides are equal and parallel.
- In a rhombus, the diagonals bisect each other at right angles and are not necessarily equal, which fits the given diagonal lengths.
- A rectangle has equal diagonals, which is not the case here.
- A kite has two pairs of adjacent sides that are equal, but does not fit the diagonal criteria.
Achievers Section
Q46: A cube has the numbers 1, 2, 2, 3, 4, and 5 on its six faces. If the cube is rolled once, what is the probability of getting:
(i) an even number
(ii) an even prime number
(iii) a multiple of 3?
(a) 1/2, 1/3, 1/6
(b) 1/2, 1/3, 1/4
(c) 2/3, 1/3, 1/6
(d) 1/2, 1/4, 1/3
 View Answer
View Answer 
Ans:(a)
- Even numbers: The even numbers on the cube are 2, 2, and 4. There are 3 even numbers out of 6 faces, so the probability is 3/6 = 1/2.
- Even prime numbers: The only even prime number is 2. There are 2 faces with the number 2, so the probability is 2/6 = 1/3.
- Multiples of 3: The only multiple of 3 on the cube is 3. There is 1 face with the number 3, so the probability is 1/6.
Q47: Height of a building is 9m and this building is represented by 9 cm on a map. What is the scale used for the map?
(a) 100 : 10
(b) 10 : 1
(c) 100 : 1
(d) 1 : 100
 View Answer
View Answer 
Ans:(d)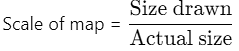
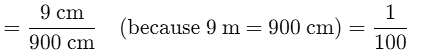 Thus, scale is 1 : 100.
Thus, scale is 1 : 100.
Q48: If F = 4 and V = 3, then the value of E is (Use Euler's formula):
(a) 7
(b) 5
(c) 4
(d) 1
 View Answer
View Answer 
Ans: (b)
∴ F = 4 and V = 3
We have Euler's formula as:
F + V = E + 2
⇒ 4 + 3 = E + 2
⇒ E = 5
Q49: Select the accurate statement.
(a) The lengths of the diagonals in a rectangle are the same.
(b) Square, rectangle, and rhombus are distinct forms of parallelograms.
(c) The diagonals of a square intersect at right angles and bisect each other.
(d) All of the above
 View Answer
View Answer 
Ans:(d)
- All the statements provided are true regarding the properties of shapes.
- The lengths of the diagonals in a rectangle are indeed equal.
- It is correct that a square, rectangle, and rhombus are all different types of parallelograms.
- Additionally, the diagonals of a square do intersect at right angles and are perpendicular bisectors of each other.
- Since all statements are accurate, the correct answer is All of the above.
Q50: Read the given statements carefully and state T for true and F for false.
(i) The number of terms in the product of (4x + y) and (6x2 + 5xy - y2) is 5.
(ii) The value of 4q2 x (5pq + p2 - 6q2) is -528, if p = 1 and q = -2.
(iii) On multiplying (5b + 2bc - c - 3) by 5abc, we get 25ab2c - 10abc2 + 5a2bc - 3abc.
(a) T T F
(b) F T T
(c) F T F
(d) T F T
 View Answer
View Answer 
Ans:(C)
- Statement (i): The product of (4x + y) and (6x² + 5xy - y²) results in 5 terms, which is true.
- Statement (ii): When substituting p = 1 and q = -2 into 4q² x (5pq + p² - 6q²), the value is indeed -528, making this statement true.
- Statement (iii): The multiplication of (5b + 2bc - c - 3) by 5abc does not yield the stated expression, hence this statement is false.
|
42 videos|82 docs|61 tests
|
FAQs on Mathematics Olympiad Previous Year Papers - 1 - Mathematical Olympiad Class 8
| 1. What topics are typically covered in the Class 8 Mathematics Olympiad exam? |  |
| 2. How can I prepare effectively for the Class 8 Mathematics Olympiad? |  |
| 3. What is the format of the Mathematics Olympiad exam for Class 8? |  |
| 4. Are there any recommended books or resources for Class 8 Mathematics Olympiad preparation? |  |
| 5. What is the importance of participating in the Mathematics Olympiad for Class 8 students? |  |




















