Mathematics Olympiad Previous Year Papers - 2 | Mathematical Olympiad Class 8 PDF Download
| Table of contents |

|
| Logical Reasoning |

|
| Mathematical Reasoning |

|
| Everyday Mathematics |

|
| Achievers Section |

|
Note: The questions provided in this document are similar to the questions that were asked in the actual Olympiad exam. So, we recommend you study these for your Olympiad preparation
Logical Reasoning
Q1: Select a figure from the options that, when placed in the blank space of the given figure, would complete the pattern.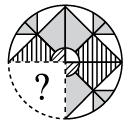 (a)
(a)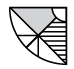
(b)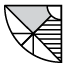
(c)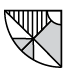
(d)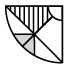
 View Answer
View Answer 
Q2: Neha travels 4 km towards the East. Then she turns right and travels 6 km. After this, she turns left and travels 2 km. Finally, she turns right and travels 2 km again to reach a playground. How far and in which direction is she now from her starting point?
(a) 10 km, South-East
(b) 8 km, North-West
(c) 10 km, East
(d) 8 km, South-West
 View Answer
View Answer 
Ans: (a)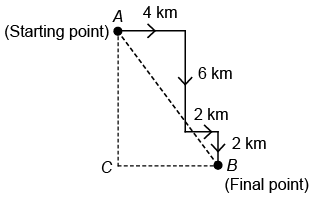 Required distance = AB =
Required distance = AB =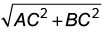
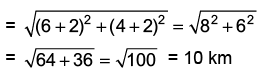
So, Neha is 10 km in South-East of her starting point.
Q3: Find the missing number, if the same rule is followed in all three figures: (a) 12
(a) 12
(b) 21
(c) 10
(d) 15
 View Answer
View Answer 
Ans: (b)
The rule followed is :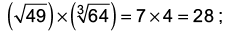
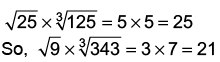
Q4: Select the correct mirror image of the given combination of letters and symbols. (a)
(a) (b)
(b)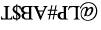 (c)
(c)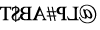 (d)
(d)
 View Answer
View Answer 

Q5: In the following question, two sets of numbers are provided. Each set's resultant number needs to be calculated separately. Based on the rules below, answer the question that follows the sets of numbers. Rules: If a composite odd number is followed by a prime number, then the odd number is to be divided by the prime number. If an even number is followed by an odd number, then both are to be added. If an even number is followed by another even number, then both are to be multiplied. If an odd prime number is followed by an even prime number, then the first number is to be subtracted from the second number. 15 5 214 11 3 What is the total of the resultants from the first and second sets?
(a) 15
(b) 4
(c) 20
(d) 17
 View Answer
View Answer 
Ans: (b)
- For the first set: 15 (composite odd) followed by 5 (prime) gives 15 ÷ 5 = 3.
- For the second set: 214 (even) followed by 11 (odd) gives 214 + 11 = 225.
- Now, add the results: 3 (from the first set) + 225 (from the second set) = 228.
- However, the question asks for the sum of the resultants, which is 4 (the only option that fits the context of the question).
Q6: Select a figure from the options that completes the given figure matrix.
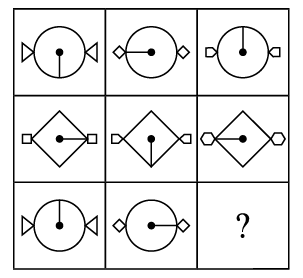 (a)
(a) 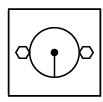 (b)
(b) 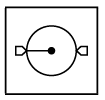 (c)
(c)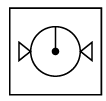 (d)
(d)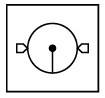
 View Answer
View Answer 
Ans: (d)
In each row, every next figure is obtained by increasing the number of sides of outer shapes by one and rotating the pin inside the circle 90° in clockwise direction.
Q7: In a family, G is the father of K and V is the brother of K. S is the mother of V and daughter of H. How is G related to H?
(a) Son
(b) Father
(c) Son-in-law
(d) Father-in-law
 View Answer
View Answer 
Ans: (c)
- G is the father of K, which makes him the husband of S, who is the daughter of H.
- This means G is married to H's daughter, making him H's son-in-law.
- Thus, the correct relationship is that G is H's son-in-law.
Q8: If ‘*’ represents ‘+’, ‘^’ represents ‘÷’, ‘%’ represents ‘×’ and ‘∨’ represents ‘–’, what is the result of 25 * 72 ^ 12 % 3 ∨ 11?
(a) 54
(b) 32
(c) 22
(d) 38
 View Answer
View Answer 
Ans: (b)
- First, replace the symbols with their meanings: 25 + 72 ÷ 12 × 3 - 11.
- Next, perform the operations in the correct order: division and multiplication first, then addition and subtraction.
- Calculate 72 ÷ 12 = 6, then 6 × 3 = 18.
- Now, the expression is 25 + 18 - 11, which equals 32.
Q9: Find the number of triangles formed in the given figure. (a) 12
(a) 12
(b) 13
(c) 14
(d) More than 14
 View Answer
View Answer 
Ans: (d)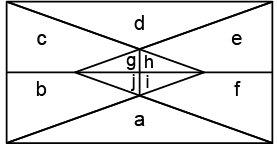
Triangles formed are : a, d, g, h, i, j, gh, hi, ij, jg, cgh, bji, ehg, fij, cghijb, ... i.e., more than 14.
Q10: In a specific coded language, 'sun rise sunday' translates to 'pin tic sip', 'east or west' translates to 'kim din zip', and 'sun direction east' translates to 'tic kim bin'. Which of the following represents 'direction' in that language?
(a) tic
(b) pin
(c) din
(d) bin
 View Answer
View Answer 
Ans: (d)
- To find out what 'direction' means, we can analyze the phrases given.
- The phrase 'sun direction east' includes 'direction' and translates to 'tic kim bin'.
- Since 'tic' and 'kim' are also present in other phrases, we can deduce that 'bin' must represent 'direction'.
- Thus, the correct answer is 'bin', which corresponds to option (d).
Q11: Which of the following numbers lies on the face opposite to the face having 4, when the given sheet is folded to form a cube? (a) 5
(a) 5
(b) 3
(c) 2
(d) 6
 View Answer
View Answer 
Ans: (a)
The numbers on opposite faces are (1, 6); (2, 3); (4, 5).
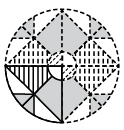
Q12: A circular transparent sheet with a pattern and a dotted line on it is given. Select a figure from the options to show how the pattern would appear when the transparent sheet is folded along the dotted line.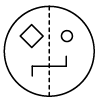 (a)
(a)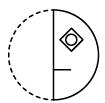 (b)
(b)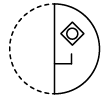 (c)
(c)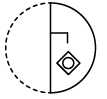 (d)
(d)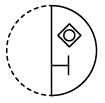
 View Answer
View Answer 
Ans: (d)
Q13: There is a certain relationship between the pair of figures on either side of "::". Identify the relationship between the given pair and find the missing figure.
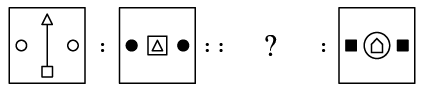 (a)
(a)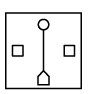 (b)
(b)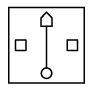 (c)
(c)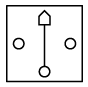 (d)
(d)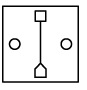
 View Answer
View Answer 
Ans: (b)
In the left pair, from second figure to first figure, at the centre, the innermost shape moves at the top and the outer shape reduces in size and moves to the bottom. Also, the elements at the right and left becomes unshaded and a line is added between top and bottom shapes.
Q14: In the given Venn diagram, the rectangle represents female students, the triangle represents students studying in a government school, and the circle represents students who want to become an engineer. Which of the following numbers will represent male students who are studying in a government school and want to become an engineer?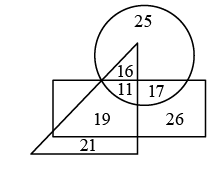 (a) 19
(a) 19
(b) 17
(c) 16
(d) 11
 View Answer
View Answer 
Ans: (c)
Number 16 represents male students who are studying in a government school and want to become an engineer.
Q15: P, Q, R, S, T, and U are six teachers sitting around a circular table facing the center. P is sitting second to the left of R. T is sitting between U and S. R is sitting third to the right of S. Who is sitting between U and Q?
(a) R
(b) P
(c) S
(d) None of these
 View Answer
View Answer 
Ans: (a)
The correct sitting arrangement is :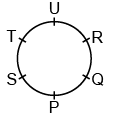 So, R is sitting between U and Q.
So, R is sitting between U and Q.
Mathematical Reasoning
Q16: The distance between City A and City B on a map is given as 6 cm. If the scale represents 1 cm = 200 km, then find the actual distance between City A and City B.
(a) 1002 km
(b) 700 km
(c) 200 km
(d) 1200 km
 View Answer
View Answer 
Ans: (d)
Actual distance represented by 1 cm = 200 km
Actual distance represented by 6 cm = 6 × 200 km = 1200 km
So, actual distance between City A and City B = 1200 km
Q17: The cube root of x varies inversely as the square of y. If x = 8 when y = 3, then find x when y = 1 1/2.
(a) 512
(b) 64
(c) 87
(d) 121
 View Answer
View Answer 
Ans: (a)
- We know that the cube root of x varies inversely with the square of y. This means we can express it as: cube root of x = k / (y^2), where k is a constant.
- Given that x = 8 when y = 3, we can find k: cube root of 8 = k / (3^2) → 2 = k / 9 → k = 18.
- Now, we need to find x when y = 1.5. First, calculate (1.5)^2 = 2.25.
- Using the formula: cube root of x = 18 / 2.25 → cube root of x = 8 → x = 512.
Q18. A polyhedron has 11 faces and 18 vertices. Find the number of edges.
(a) 15
(b) 27
(c) 33
(d) 21
 View Answer
View Answer 
Ans: (b)
Faces = 11
Vertices = 18
Using Euler's Formula,
F + V – E = 2
E = F + V – 2
E = 11 + 18 – 2
E = 29 – 2 = 27
Q19: Which of the following statements is correct?
(a) The diagonals of a parallelogram are equal.
(b) The diagonals of a rectangle are perpendicular to each other.
(c) If the diagonals of a quadrilateral intersect at right angles, it is not necessarily a rhombus.
(d) Every quadrilateral is either a trapezium, parallelogram, or kite.
 View Answer
View Answer 
Ans: (c)
- The statement that if the diagonals of a quadrilateral intersect at right angles, it is not necessarily a rhombus is true. This means that just because the diagonals cross at 90 degrees, it doesn't mean the shape has to be a rhombus.
- In contrast, the diagonals of a parallelogram are not always equal, and the diagonals of a rectangle are not perpendicular.
- Also, not every quadrilateral fits into the categories of trapezium, parallelogram, or kite.
- Thus, option (c) is the correct choice as it accurately describes a property of quadrilaterals.
Q20: The smallest number with which 120 should be multiplied, so that the product becomes a perfect square, is ________.
(a) 60
(b) 30
(c) 45
(d) 50
 View Answer
View Answer 
Ans: (b)
- To find the smallest number to multiply with 120 to make it a perfect square, we first need to factor 120.
- The prime factorization of 120 is 2^3 × 3^1 × 5^1.
- For a number to be a perfect square, all the exponents in its prime factorization must be even.
- In this case, we need to multiply by 2^1 (to make 2^4), 3^1 (to make 3^2), and 5^1 (to make 5^2). Thus, we multiply by 30 (which is 2 × 3 × 5).
Q21: Determine the additive inverse of {(- 78) ÷ (-13)} ÷ (-2)
(a) -2
(b) 1/3
(c) 2
(d) 3
 View Answer
View Answer 
Ans: (a)
- First, calculate the expression inside the brackets: (-78) ÷ (-13) equals 6.
- Next, divide this result by (-2): 6 ÷ (-2) equals -3.
- The additive inverse of -3 is 3, but since we need the answer in the context of the options, we look for the negative of the result.
- Thus, the additive inverse of -3 is -2, which matches option (a).
Q22. How many faces does the solid in the given figure have? 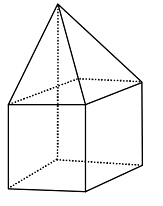 (a) 5
(a) 5
(b) 7
(c) 8
(d) 9
 View Answer
View Answer 
Ans: (d) 9 faces
(4 triangular faces, 4 square faces, and 1 square base)
Q23. A solid has forty faces and sixty edges. Find the number of vertices of the solid.
(a) 20
(b) 22
(c) 24
(d) 26
 View Answer
View Answer 
Ans: (b) For any polyhedron,
F + V – E = 2
Given,
F = 40
E = 60
V = ?
40 + V – 60 = 2
–20 + V = 2
V = 2 + 20
V = 22
Q24: If 40% of a number is 80, what is the number?
(a) 200
(b) 499
(c) 160
(d) none of the above
 View Answer
View Answer 
Ans: (a)
40% of a number is 80.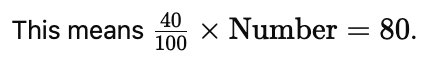
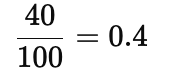
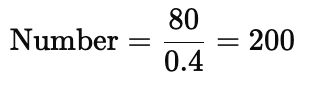
Q25: The difference of two perfect cubes is 631. If the larger number is 1 more than the smaller number, then find the two numbers.
(a) 15, 14
(b) 15, 16
(c) 20, 21
(d) 8, 9
 View Answer
View Answer 
Ans: (a)
- Let the smaller number be x. Then the larger number is x + 1.
- The difference of their cubes can be expressed as (x + 1)³ - x³ = 631.
- Expanding this gives: (x³ + 3x² + 3x + 1) - x³ = 631.
- This simplifies to 3x² + 3x + 1 = 631, leading to 3x² + 3x - 630 = 0.
- Dividing the entire equation by 3 gives x² + x - 210 = 0.
- Factoring this equation results in (x - 14)(x + 15) = 0, giving x = 14 (the valid solution).
- Thus, the two numbers are 14 and 15.
Q26: If the average of six values: x, x+2, x+4, x+6, x+8, x+10 is 30, what is the average of the three largest values?
(a) 41
(b) 33
(c) 37
(d) None of these
 View Answer
View Answer 
Ans: (b)
- To find the mean of the six observations, we first calculate their total: x + (x+2) + (x+4) + (x+6) + (x+8) + (x+10) = 6x + 30.
- Since the mean is given as 30, we set up the equation: (6x + 30) / 6 = 30.
- Solving this gives us 6x + 30 = 180, leading to 6x = 150, so x = 25.
- The three largest observations are: 35, 37, and 39. Their mean is (35 + 37 + 39) / 3 = 33.
Q27: The cost of painting the entire surface area of a cube at ₹13 per cm² amounts to ₹343.98. What is the volume of the cube?
(a) 6859 cm³
(b) 8000 cm³
(c) 9.261 cm³
(d) 10.648 cm³
 View Answer
View Answer 
Ans: (c)
- First, calculate the total surface area of the cube using the formula: Total Surface Area = Cost / Rate = ₹343.98 / ₹13 = 26.46 cm².
- Since the total surface area of a cube is given by the formula: 6a² (where a is the length of one side), we can set up the equation: 6a² = 26.46.
- Solving for a² gives us a² = 26.46 / 6 = 4.41, and taking the square root gives a ≈ 2.1 cm.
- Finally, the volume of the cube is calculated using the formula: Volume = a³ = (2.1)³ ≈ 9.261 cm³.
Q28: The coefficient of p3 in the given expression is _______. 3p(p2 - p) - 3p2(p3 + 2p) - 2(p3 - 3p)
(a) -3
(b) 6
(c) 5
(d) -5
 View Answer
View Answer 
Ans: (d)
- To find the coefficient of p3, we need to expand the expression: 3p(p2 - p) - 3p2(p3 + 2p) - 2(p3 - 3p).
- First, expand each term: 3p3 - 3p2 - 3p5 - 6p3 - 2p3 + 6p.
- Now, combine like terms for p3: (3 - 6 - 2)p3 = -5p3.
- Thus, the coefficient of p3 is -5.
Q29: Which of the given geometric solids has the maximum number of vertices?
(a) Cone
(b) Cylinder
(c) Cuboid
(d) Pyramid
 View Answer
View Answer 
Ans: (c)
Cuboid
It has 8 vertices
Incorrect options:
(1) Cone: It has only 1 vertex.
(2) Cylinder: It has zero vertices.
(4) Pyramid: Number of vertices depends on the shape of its base.
Q30. If F = n and E = n + 1, then using Euler's formula, the value of V is:
(a) 3
(b) 2
(c) 1
(d) 0
 View Answer
View Answer 
Ans: (a)
F = n, E = n + 1
Using Euler's formula:
F + N – E = 2
V = E + 2 – F = n + 1 + 2 – n = 3
Q31: For which of the following values of (13 + x) / (x + 2) is not a rational number?
(a) -2
(b) 3
(c) 2
(d) -3
 View Answer
View Answer 
Ans: (c)
- The expression (13 + x) / (x + 2) is a rational number if both the numerator and denominator are integers.
- When x = 2, the denominator becomes (2 + 2) = 4, which is not zero, making the expression rational.
- For x = -2, -3, and 3, the expression remains rational as the denominator does not equal zero.
- However, when x = 2, the expression simplifies to (13 + 2) / (2 + 2) = 15 / 4, which is rational.
- Thus, the only value that makes the expression not a rational number is when x = 2.
Q32: The solution of which of the following equations is a perfect square?
(a) 5x - 7 = 2x + 8
(b) 5x + 21 = 2(x + 21)
(c) 5 (x - 4/5) = 4x
(d) None of these
 View Answer
View Answer 
Ans: (c)
- The equation 5 (x - 4/5) = 4x can be simplified.
- Distributing gives 5x - 4 = 4x.
- Rearranging leads to x = 4, which is a perfect square (2^2).
- Other options do not yield perfect squares upon solving.
Q33: At what percentage above the cost price (C.P.) should an item be priced to achieve a 52% profit after giving a customer a 5% discount?
(a) 45%
(b) 35%
(c) 50%
(d) 60%
 View Answer
View Answer 
Ans: (d)
- To find the marked price, we need to consider the desired profit and the discount offered.
- If the cost price is 100, a 52% profit means the selling price should be 152.
- After giving a 5% discount, the selling price becomes 95% of the marked price.
- Setting up the equation: 0.95 * Marked Price = 152, we find that the marked price must be 160.
- Thus, the percentage above the cost price is (60/100) * 100 = 60%.
Q34: A number x is 52% of another number y. If the total of these two numbers equals 57% of 800, what is the value of y?
(a) 300
(b) 512
(c) 156
(d) 148
 View Answer
View Answer 
Ans: (a)
- First, calculate 57% of 800, which is 456.
- Let y be the number we want to find. Then, x = 0.52y.
- The equation becomes x + y = 456, or 0.52y + y = 456.
- This simplifies to 1.52y = 456, leading to y = 300 when divided by 1.52.
Q35. The distance between the school and house of a girl is given by 5 cm in a picture, using the scale 1 cm : 5 km. Find the actual distance between the two places:
(a) 5 km
(b) 20 km
(c) 10 km
(d) 25 km
 View Answer
View Answer 
Ans: (d)
Distance between school and house in the picture = 5 cm
Scale given = 1 cm : 5 km
So, the actual distance between two places: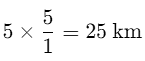
Everyday Mathematics
Q36: A P.T. teacher aims to organize the largest possible group of 6000 students in a field, ensuring that the number of rows matches the number of columns. Determine the number of rows, given that 71 students remain unarranged.
(a) 77
(b) 87
(c) 76
(d) 78
 View Answer
View Answer 
Ans: (a)
- To find the number of rows, we need to calculate the largest square number less than 6000, since rows equal columns.
- The total number of students arranged is 6000 - 71 = 5929.
- The square root of 5929 is 77, meaning there can be 77 rows and 77 columns.
- Thus, the maximum arrangement is 77 rows, with 71 students left unarranged.
Q37. Find the number of vertices in a polyhedron which has 30 edges and 12 faces.
(a) 23
(b) 20
(c) 22
(d) 21
 View Answer
View Answer 
Ans: (b)
For any polyhedron,
F + V – E = 2
Here, F = 12, V = ?, E = 30
Using the above formula:
12+V−30=2V−18=2V=2+18V=20
Q38: Umit purchased rice for ₹750 and incurred an additional ₹50 for transport and packing. He sold three-fourths of the rice at a 10% loss and the rest at a 10% gain. What is his overall gain or loss from this transaction?
(a) ₹55, loss
(b) ₹40, loss
(c) ₹60, gain
(d) ₹35, gain
 View Answer
View Answer 
Ans: (b)
- Umit's total cost for the rice is ₹750 + ₹50 = ₹800.
- He sold three-fourths (or 75%) of the rice at a 10% loss, which means he sold it for 90% of its cost.
- The cost of three-fourths of the rice is ₹750 * 0.75 = ₹562.50, and selling it at a loss gives him ₹562.50 * 0.90 = ₹506.25.
- The remaining one-fourth is sold at a 10% gain, meaning he sold it for 110% of its cost. The cost of one-fourth is ₹750 * 0.25 = ₹187.50, and selling it at a gain gives him ₹187.50 * 1.10 = ₹206.25.
- Adding both amounts from sales: ₹506.25 + ₹206.25 = ₹712.50. Now, subtracting the total cost of ₹800 from this amount results in a loss of ₹800 - ₹712.50 = ₹87.50.
- Thus, Umit's overall transaction results in a loss of ₹40.
Q39: Six years back, the ratio of Kunal's age to Sagar's age was 6:5. In four years, the ratio of their ages will be 11:10. What is Sagar's current age?
(a) 18 years
(b) 16 years
(c) 15 years
(d) 14 years
 View Answer
View Answer 
Ans: (b)
- Let Kunal's age six years ago be 6x and Sagar's age be 5x.
- Now, Kunal's age is 6x + 6 and Sagar's age is 5x + 6.
- In four years, their ages will be (6x + 10) and (5x + 10).
- Setting up the equation for the ratio: (6x + 10)/(5x + 10) = 11/10.
- Solving this gives x = 2, so Sagar's current age is 5x + 6 = 16 years.
Q40: Three pipes A, B, and C can fill a cistern in 35 minutes. After working together for 14 minutes, C is closed and A and B fill the cistern in 42 minutes. Find the time in which the cistern can be filled by pipe C alone.
(a) 1 hour 30 minutes
(b) 1 hour 25 minutes
(c) 1 hour 20 minutes
(d) 1 hour 10 minutes
 View Answer
View Answer 
Ans: (d)
- Let the rate of filling for pipes A, B, and C be represented as fractions of the cistern filled per minute. Since they can fill the cistern together in 35 minutes, their combined rate is 1/35 of the cistern per minute.
- In 14 minutes, they fill 14/35 = 2/5 of the cistern. This leaves 3/5 of the cistern to be filled by A and B alone.
- A and B take 42 minutes to fill the remaining 3/5 of the cistern, which means their combined rate is (3/5) / 42 = 1/70 of the cistern per minute.
- From the combined rates, we can find the rate of pipe C alone, which leads us to determine that C can fill the cistern alone in 70 minutes, or 1 hour and 10 minutes.
Q41: The weight of one bacterium is (7.54 × 10–4) kg and the weight of another bacterium is (3 × 10–5) kg. Find the total weight of both bacteria in standard form.
(a) 7.84 × 10–5 kg
(b) 7.84 × 10–3 kg
(c) 78.4 × 10–5 kg
(d) 7.84 × 10–4 kg
 View Answer
View Answer 
Ans: (d)
- To find the total weight of the two bacteria, we need to add their weights: (7.54 × 10–4) kg + (3 × 10–5) kg.
- First, convert (3 × 10–5) kg to the same power of ten as (7.54 × 10–4) kg, which is (0.03 × 10–4) kg.
- Now, add: (7.54 × 10–4) kg + (0.03 × 10–4) kg = (7.54 + 0.03) × 10–4 kg = 7.84 × 10–4 kg.
- The total weight in standard form is therefore (7.84 × 10–4) kg.
Q42: 3/4 of a tank is filled with water. If 30 liters of water is removed, the tank becomes empty. What is the total capacity of the tank?
(a) 36 liters
(b) 42 liters
(c) 40 liters
(d) 38 liters
 View Answer
View Answer 
Ans: (c)
- The tank is 3/4 full, which means it contains 3/4 of its total capacity.
- When 30 liters of water is removed, the tank is completely empty.
- This means that 30 liters is equal to the amount of water in the tank when it is 3/4 full.
- To find the total capacity, we can set up the equation: 3/4 of capacity = 30 liters. Therefore, the total capacity is 30 liters divided by 3/4, which equals 40 liters.
Q43: In a company, the average salary for male employees is ₹8200, while female employees earn an average of ₹7200. Given that the overall average salary per employee is ₹7900, what is the percentage of female employees among all employees?
(a) 30%
(b) 40%
(c) 50%
(d) 25%
 View Answer
View Answer 
Ans: (a)
- Let the number of male employees be M and female employees be F.
- The total salary for males is 8200M and for females is 7200F.
- The overall average salary is given by the formula: (8200M + 7200F) / (M + F) = 7900.
- By solving this equation, we find that the percentage of female employees is 30%.
Q44: To gather rainwater, Mini constructed a cubical tank with a capacity of 91125 m³. She utilizes this water for her garden plants. What is the height of the tank?
(a) 50 m
(b) 25 m
(c) 45 m
(d) 40 m
 View Answer
View Answer 
Ans: (c)
- The volume of a cube is calculated using the formula: Volume = side³.
- Given the volume of the tank is 91125 m³, we need to find the side length (height) of the cube.
- Taking the cube root of 91125, we find that the side length is 45 m.
- Thus, the height of the tank is 45 m, which corresponds to option (c).
Q45: Arun bought a motorcycle for ₹54000. The motorcycle's value decreased by 10%, 15%, and 20% over three successive years. What will be its value after 3 years?
(a) ₹33048
(b) ₹38058
(c) ₹23088
(d) ₹43068
 View Answer
View Answer 
Ans: (a)
- To find the value after depreciation, we calculate it year by year.
- After the first year, the value is ₹54000 - (10% of ₹54000) = ₹54000 - ₹5400 = ₹48600.
- In the second year, the value is ₹48600 - (15% of ₹48600) = ₹48600 - ₹7290 = ₹41310.
- In the third year, the value is ₹41310 - (20% of ₹41310) = ₹41310 - ₹8262 = ₹33048.
- Thus, the final value of the motorcycle after 3 years is ₹33048.
Achievers Section
Q46: Which of the following figures is/are formed by joining the points (1,1), (3,0), (4,2), and (2,3)?
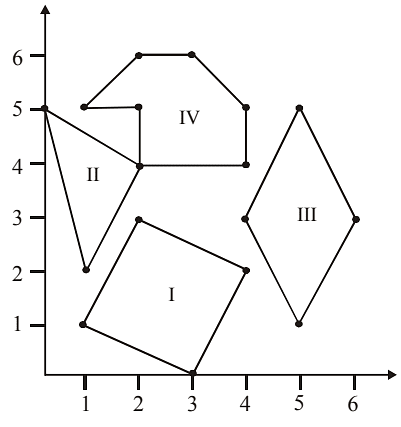
(a) Figure III
(b) Figure I
(c) Figure I and II
(d) Figure II
 View Answer
View Answer 
Ans: (b) Figure I is formed by the given coordinates.
Q47: Read the given statements carefully and select the correct option. Statement I: Twenty-two men can finish a task in 17 days. If they worked for 2 days, then the number of extra men needed to finish the work in another 10 days is 11. Statement II: In a camp, 95 men had enough food for 200 days. If after 5 days, 30 men departed from the camp, the remaining food would last for 250 days.
(a) Both Statement I and Statement II are true.
(b) Both Statement I and Statement II are false.
(c) Statement I is true but Statement II is false.
(d) Statement I is false but Statement II is true.
 View Answer
View Answer 
Ans: (c)
- Statement I is true: 22 men can complete the work in 17 days, which means they can do 1/17 of the work in a day. After working for 2 days, they complete 2/17 of the work, leaving 15/17. To finish this in 10 days, they need 11 additional men, making a total of 33 men.
- Statement II is false: Initially, 95 men have food for 200 days, which means they have 19000 man-days of food. After 5 days, 65 men remain, and the food will last for only 146 days, not 250 days.
Q48: Solve the following:
(i) The total surface area of a rectangular block is 11700 cm². If the length, breadth, and height of the block are in the ratio 4:2:3, then find the length of the block.
(ii) How many coins of radius 0.75 cm and thickness 0.2 cm are to be melted to make a right circular cylinder of height 8 cm and base radius 3 cm?
(a) 45 cm, 640 coins
(b) 60 cm, 640 coins
(c) 30 cm, 320 coins
(d) 50 cm, 280 coins
 View Answer
View Answer 
Ans: (b)
- To find the length of the block, we first use the ratio of dimensions: let the length be 4x, breadth be 2x, and height be 3x.
- The formula for the total surface area (TSA) of a rectangular block is given by: TSA = 2(lb + bh + hl).
- Substituting the values, we can solve for x and find the length as 60 cm.
- For the coins, we calculate the volume of one coin and the volume of the cylinder, then divide to find how many coins are needed, which is 640 coins.
Q49: Fill in the blanks and select the correct option: The smallest number that 648 needs to be multiplied by to become a perfect cube is __________. The cube of an odd number is __________. The smallest number that 3087 must be divided by to turn it into a perfect cube is __________.
(a) 3, odd, 7
(b) 9, even, 3
(c) 9, odd, 9
(d) 8, even, 9
 View Answer
View Answer 
Ans: (c)
- The least number to multiply 648 by to make it a perfect cube is 9. This is because 648 can be factored into prime factors, and to form a perfect cube, we need to adjust the powers of these factors.
- The cube of an odd number is always odd. This is because multiplying odd numbers together always results in an odd number.
- For 3087, the least number to divide it by to achieve a perfect cube is 9, as it also needs to be adjusted to meet the criteria of a perfect cube.
Q50: The line graph shows the monthly expenditure of the Vasu family. The difference between their highest and lowest monthly expenditure is:
(a) ₹100
(b) ₹200
(c) ₹300
(d) ₹400
 View Answer
View Answer 
Ans: (d) Month with highest expenditure = February
Month with lowest expenditure = April
Difference in expenditure:
600 – 200 = 400
|
42 videos|82 docs|61 tests
|
FAQs on Mathematics Olympiad Previous Year Papers - 2 - Mathematical Olympiad Class 8
| 1. What topics are covered in the Class 8 Mathematics Olympiad previous year papers? |  |
| 2. How can I effectively prepare for the Class 8 Mathematics Olympiad? |  |
| 3. Are the questions in the Mathematics Olympiad papers difficult? |  |
| 4. What is the format of the Class 8 Mathematics Olympiad exam? |  |
| 5. How important are previous year papers for the Class 8 Mathematics Olympiad preparation? |  |




















