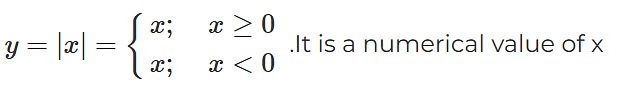Functions from Algebra: Basic Concepts and Application | Quantitative for GMAT PDF Download
Introduction
Certain kind of questions from algebra requires higher levels of algebraic concepts. However, such questions can also be easily solved by using alternate approaches from graphs.
Below are a few questions from GMAT and other exams, which would be very difficult to crack if we try solving them using the concepts from algebra.
- Find the number of real solutions of x for the equation 2x = x2
- Find the number of integral solutions the equation |x-1| + |x+3| +|x-5| <20
- How many integral pairs (x, y) are there such that |x|+|y|=4
- Find the minimum value of y if y=|1-|x+3||
As mentioned in the introduction, all of the above four questions can be solved by using the concept of algebra. But if we have the basic idea of the graphs of some special functions and a good understanding of the transformation of the graphs, then we can solve complex looking questions easily.
Let us understand some special functions which appear very frequently.
Identity function/ graph of f(x)=x
A function f defined by f(x) = x for all real value of x, is called the identity function.If you refer to the graph, you will find that it is nothing but a straight line passing through the origin and inclined an angle of 45° with the x-axis. Algebraically, we can also represent it as y=x.
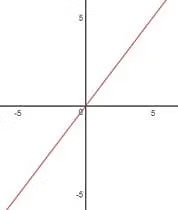
Graph of f(x)=x2
A function given by f(x)=x2 is called the square function. Clearly, y=x2 is a parabola and it’s also an even function, so it is symmetrical about y-axis as shown in the figure:
A function given by f(x)=x2 is called the square function.
Clearly, y=x2 is a parabola and it’s also an even function, so it is symmetrical about y-axis as shown in the figure:
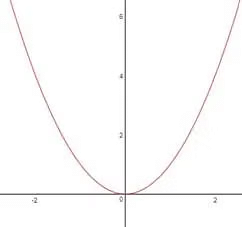
Graph of f(x)=x3
A function given by f(x)=x3 ,f(x)=x3 is called the cube function. When a function is an odd function, its graph is symmetrical about the opposite quadrant or we can say that the graph is symmetrical about the origin as shown in the figure:
A function given by f(x)=x3is called the cube function. When a function is an odd function, its graph is symmetrical about the opposite quadrant or we can say that the graph is symmetrical about the origin as shown in the figure:
On analyzing and extending the logic of the above three graph, we can generalize the following:
Graph of f(x)=x2n; Where n is a natural number
This will always be an even function. Hence, the graph of f(x)=x2n will always be symmetrical about the y-axis.
The below figure shows graphs of the function for some values of n.
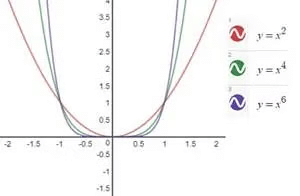
Graph of f(x)=x2n-1; Where n is a natural number
This will always be an odd function. Hence, the graph of f(x)=x2n-1 will always be symmetrical about the origin or opposite quadrants.
The below figure shows graphs of the function for some values of n.
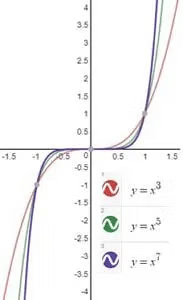
Graphs of Rational Expressions
Rational functions are the functions obtained by dividing a polynomial by another polynomial, i.e.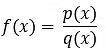
In the exam, we don’t get complicated rational expressions. Rather, we get simple rational expression functions, and their graphs are easy to plot as well.
Let us take some elementary rational functions and their corresponding graphs.
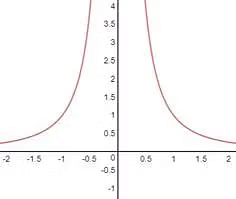
1. Graph of f(x)=1/x
This is also called the reciprocal function or a rectangular hyperbola. This is also an odd function so its graph is symmetrical about the opposite quadrant.
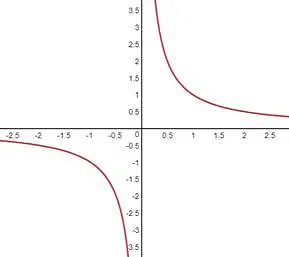
2. Graph of f(x)= 1/x2
Since the power of x is even, clearly, this is an even function. So it must be symmetrical about the y-axis. Also, even negative values of the function f(x) will always be positive. It is also important to mention here that the domain of the function will be all real values except 0. that is, it cannot take the value 0.
Piecewise Functions
There are a few types of functions which come under the category of piecewise functions. They are absolute value function, signum function, greatest integer function, fractional part function, least integral function etc.
For exams, we have to focus only on the absolute value function in detail.
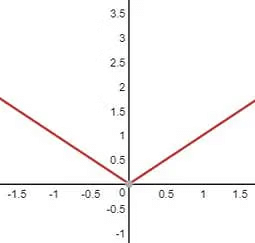
Absolute Value Function (or Modulus Function)
- It is symmetrical about y axis
Properties of modulus functions:
- |x|≤a⇒–a≤x≤a;(a≥0)
- |x|≥a⇒x≤–aorx≥a;(a≥0)
- |x±y|≥||x|–|y||
Exponential Function
The function f(x)=ax, where a≠0, and x is a real number, is called exponential function.
Depending upon the value of a, we can have all the increasing function or decreasing function.
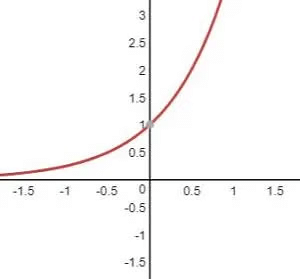
Case I: If a >1
Say, f(x)=y=4x increases with the increase in x.
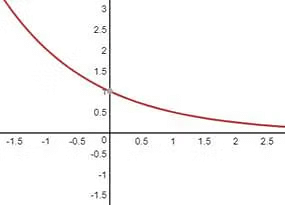
Case II: If 0< a < 1
Say, f(x)=y= (1/2)x decreases with an increase in x.
In general, exponential function increases or decreases as (a>1) or (0<a<1) respectively.
Logarithmic Function
This is an inverse of an exponential function. In other words, in the exponential function if we replace x with y and y with x, and rearrange the function taking x as the independent variable and as the dependent variable, then the new function will be a logarithmic function.
The logarithmic function is defined as f(x)=logax;(x,a>0) and a≠0. The domain of logarithmic function is all positive real number.
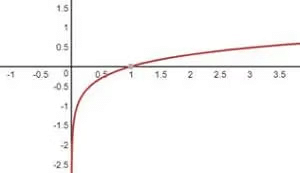
These are the graphs of basic functions which frequently appeared in the exam. Our next step is to understand the transformation of graphs.
Transformation of the Graphs
Transformation of the Graphs
Transformation of the Graphs
Transformation of function f(x) to f(x)±a
When f(x) is transformed to f(x)+a where a is positive, the graph shifts upward through ‘a’ units.And if f(x) is transformed to f(x)+a where a is negative, the graph shifts downward through ‘a’ units.
Let us understand it with the help of an example:
Say, where to plot the graph of y=|x|+3.
We know that y=|x| is plotted as below:
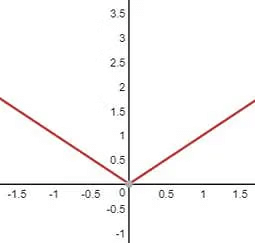
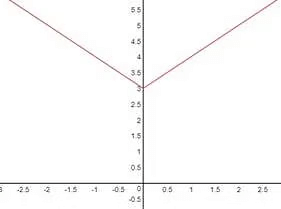
So, fo y=|x|+3, the graph will shift 2 units upward, i.e,
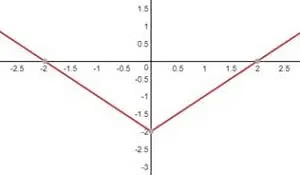
Similarly, if we have to plot y=|x| -2, the graph will shift downwards by 2 units.
Transformation of Graph from f(x) to f(x±a)
For f(x) à f(x+a), where a is positive, the graph shifts through ‘a’ units towards the left. And for f(x) à f(x-a), the graph shifts through ‘a’ units towards the right.
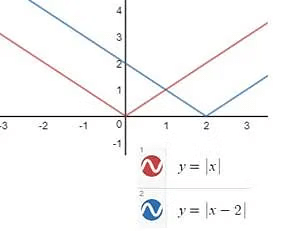
Example: Plot the graph of y=|x+3| and y=|x-2|
The graph of y=|x+3| will be:
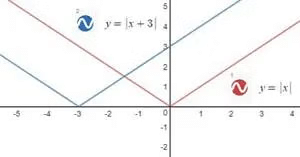
Similarly, the graph of y=|x-2| will be:
Transformation of Graph from f(x) to f(-x)
To draw y=f(-x), take the image of the curve y=f(x) in y-axis as a plane mirror. Or, turn the graph of f(x) by 1800 about the y-axis.
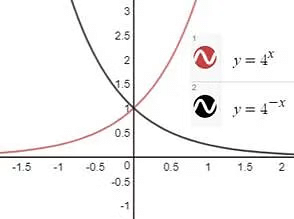
Example: Plot the graph of y=4–x, where a is positive.
We know the graph of y=4x
Taking the mirror image of the graph around the y-axis.
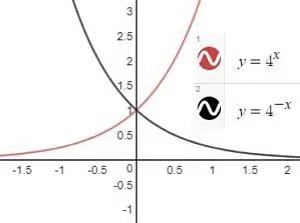
Transformation of Graph from f(x) to -f(x)
To draw y=-f(x) take image of y=f(x) in the x-axis as plane mirror. Or, turn the graph of f(x) by 1800 about x-axis.
Example: Plot the graph of y=-4x
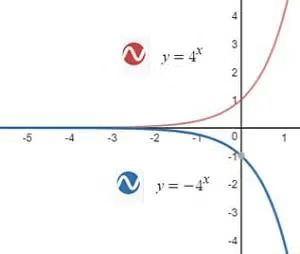
Example: Plot the graph of y=-|x|
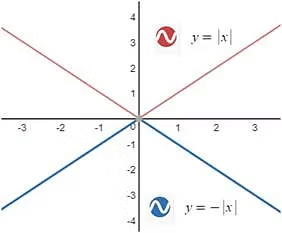
Transformation of Graph from f(x) to -f(-x)
To draw y=-f(-x) take image of f(x) about y-axis to obtain f(-x) and then take image of f(-x) about x-axis to obtain –f(-x).
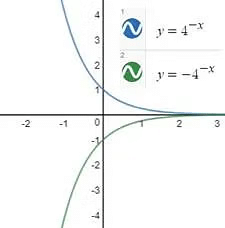
Example: Plot the graph of y=-4-x
Taking mirror image about the y-axis to get the graph of y=4-x
Taking mirror image of y=4-x about x-axis to get the y=-4-x
Transformation of Graph from f(x) to |f(x)|
The graph of |f(x)| is drawn by taking the mirror image (in x-axis) of the portion of the graph of f(x) which lies below x-axis.
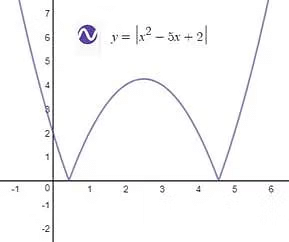
Transformation of Graph from f(x) to f(|x|)
To draw the graph of y=f(|x|), neglect the curve for x<0 and take the images of curve for x≥ 0 about the y-axis.
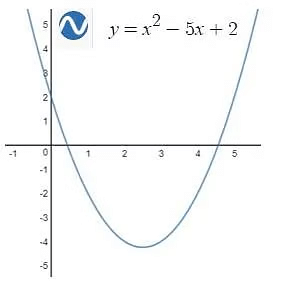
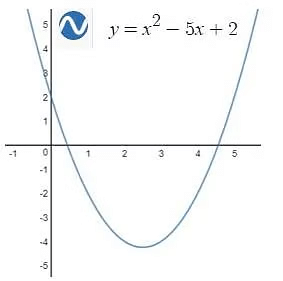
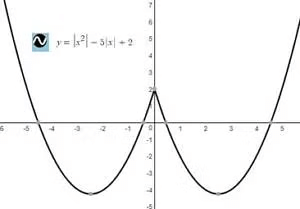
Example: Plot the graph of y=|x|2-5|x|+2
We know the graph of y=x2-5x+2
Neglecting graph for x<0 and Taking mirror image about y-axis to the part of the graph for x≥0.
Maxima and Minima Based Application
Let us examine through an example:
Example 1: There were two cat aspirants Ajay and Vijay. Ajay keeps boasting about his quant percentiles( in 90’s).One day Vijay brought a question to Ajay, it said” There is a function f(x) = ax^2 +bx +c and f(4)= 100 . If the coefficients of a,b and c are distinct positive integers, then find the maximum value ( a+b+c) can attain ? “. Can you answer it faster than Ajay?
1) 82
2) 76
3)79
4)0
Solution: Ajay started scribbling in his rough paper, let us analyze his solution:
F(x) = ax2 +bx + c, what is the functional variable in this? x right !!
so if it is given that f(4) = 100 means that by putting x=4, the function will return a value of 100.
That is f(4)= 16a + 4b + c = 100 , we are good till now right!But our requirement is finding the maximum value of (a+b+c), so the quantity with the largest coefficient has to be minimised,
16*1 +4*1 + 80 =100 (Keep in mind “positive integers” is mentioned a=1,b=1)
So the maximum value which Ajay got was 1+1+80= 82
The above result is certainly wrong and could fetch you a penalty of 1/3rd marks.
The term “DISTINCT POSITIVE INTEGERS ” is vital.
16 *1 + 4*2 + 76= 100
so maximum = (76+1+2) = 79Hope the explanation is elaborative. Let’s move to our next segment.
Identical Functions
There is a thumb rule for determining whether the given two functions are identical or not.
” The domain of f(x) should be equal to the domain of g(x) .”
Observe the following examples to get a clear scenario of the things.
Example 1: we will consider two fucntions f(x)= root(x2) and g(x) = |x|
In f(x) for every real value of x , there is a value of f(x), which means x belongs to R
In G(x) for every real value of x, there is a value of g(x), which also means x belongs to R.
In both the cases, the domain is same. Hence, The Functions are “IDENTICAL”
Example2: Now again we have two fucntions f(x)= ln (x2 -5x +6) and g(x)= ln(x-2) + ln(x-3)
The ln values cannot be negative or zero . So we will analyse botgh cases.
x2 -5x +6x >0 ⇒ (x-2)(x-3)>0 ⇒ x belongs (-infy,2)U(3,infy)
(x-2)>0 and (x-3)>0 ⇒ x>2 and x>3 ⇒ x belongs to (2, infy)
In both cases there are different domains ,so the fucntions are “NOT IDENTICAL”.
Greatest Integer Function
Questions from functions are always ghastly and require an extra effort over other topics especially in case of students without a mathematical background.
Questions related to greatest integer function have been seen very frequent in past few years in various exams and mocks.
So let us put an effort to unlock the mystery of Greatest Integer Function. Greatest Integer Function, [x] indicated the integral part of x which is nearest and smallest integer to x. It is also known as floor of x.
e.g. [9.638] = 9, [7] = 7, [0.286] = 0, [-3.432] = -4, [-0.432] = -1
In general, n = x < n+1 , where n is an integer, [x] = n
Now, we can say that for any real number x, x = I + f
where,
I = Integral Part denoted by [x]
f = Fractional Part denoted by {x}
Thus, {x} = x – [x]
Let us see some varied applications::
Example 1: Find the value of [3/4] + [3/4 + 1/100] + [3/4+ 2/100] +……..+ [3/4 + 99/100].
Solution: [3/4] + [3/4+ 1/100] + [3/4+ 2/100] +… [3/4+25/100]+[3/4+26/100]+ ? + [3/4+ 99/100]
First of all the number of terms in the series is 100.
[3/4]=[0.75]=0
[3/4 + 1/100]= [0.75 + 0.01]=[0.76]=0
similarly the frist 25 terms will be equal to 0 (as 25th term is [3/4 + 25/100]=[3/4 +1/4]=1)
and from the 26th term each term will be equal to 1.
First 25 terms are 0 and the next 75 terms are 1.
So, sum of all the terms = (25 × 0) + (75 × 1) = 75
Interesting Formula 1
Difference between CI and SI for 2 and 3 years
respectively:
(CI)– (SI)= Pa2 (for two years)
(CI)– (SI)= Pa2 (a + 3) (for three years)
where, a = r/100
Interesting Formula 2
A principal amount of X times in T years at S.I. It
will become Y times in:
Years = ((Y -1)/(X-1)) * T
A principal amount of X times in T years at C.I. It
will become Y times in:
Years = T × n
where n is given by Xn = Y
Functions in Remainders
How can you use the remainder theorem to evaluate polynomials?
Let’s first state the remainder theorem. The remainder theorem states the following:
If you divide a polynomial f(x) by (x – h), then the remainder is f(h).
The theorem states that our remainder equals f(h).
Therefore, we do not need to use long division, but just need to evaluate the polynomial when x = h to find the remainder.
A basic example to justify the above statement !
Example 1: Given that, f(x) = x3 + 2x2 – 11x – 12
Find the remainder if f(x) is divided by (x – 2)
Solution: The remainder theorem tells us that h = 2, so evaluate f(2). We replace x with 2 in the polynomial as follows:
f(2) = 23 + 2(2)2 – 11(2) – 12
We then simplify: f(2) = 8 + 8 – 22 – 12 = -18
Now let us observe a moderate level question application ::
Example 2: The polynomial p(x) satisfies
p(−x) = −p(x). When p(x) is divided by x − 3 the remainder is 6. Find the remainder when p(x) is divided by x2 − 9.
Solution: Now first inference that can be drawn is p(-x)=-p(x) which implies that it is an odd function.
According to Remainder structure, N = dq+r (N is dividend, d is dividor, q is quotient, r is remainder)
so ,p(x)=(x-3)*k+6 ((x-3) is dividend, k is divisor, 6 is remainder)
when p(x) mod x2-9
p(x)=m*(x2-9)+ax+b (as if the degree of divisor is x2 ,then remainder will be of lesser degree i.e ax+b)
now at x=3
p(x)=3a+b=6
and x=-3 remainder will be -6
p(-3)=-3a+b=-6
2b=0
so b=0 and a=2
remainder= ax+b= 2x
Example 3: If f(x) = x4 + x3 + x2 + x + 1, where x is a positive integer greater than 1.
What will be the remainder if f(x^5) is divided by f(x) ?
Solution: f(x) = x4 + x3 + x2 + x + 1.
By replacing x with x5 we get,
f(x5) = x20 + x15 + x10 + x5 + 1.
Let’s take x = 2.
f (x) = f(2) = 31.
f (x5) = f(32) = 220 + 215 + 210 + 25+1.
f(32) mod f(2) = 220 + 215 + 210 + 25+1 mod 31
= (25)4 + (25)3+(25)2 +(25) + 1 mod 31
= 1+1+1+1+1
= 5.
NOTE: You can try the same with x=3 and cross verify.But if assume x=1 , we will be lost.
Functions in Quadratics
Let us see the application of functions in algebra/Quadratic
Example 1: If 5 is root of a quadratic function of f(x)=0 and 6*f(2)=f(4)
Find another root of f(x)=0
Solution: Firstly, basics on Quadratic eqn , It has only two roots.
One of the root is given to us (ie 5) which means on substituting the value of 5
in the given f(x) it will result a 0.
Now, f(x) = ax2 +bx+c = 0
f(2) = 4a +2b +c =0
f(4)= 16a +4b+c=0
using the relation 6 * f(2)= f(4)
24a+12b +6c = 16a+4b+c
8a+8b+5c=0
and 25a+5b+c=0;
we will get a relationship between a and b, a/b = (- 17/117)
Let the other root be y
sum of roots = 5+y = (- b/a)….eqn 2
solving both the eqns y = 32 /17
Hope the explanation is !!
Pattern Application of Functions
Example 1: If f(x − 1) + f(x + 1) = f(x) and f(2) = 6, f(0) = 1, then what is the value of f(50) ?
1) −7
2) 6
3) 1
4) 7
Solution: Since we know both f(0)=1 and f(2)=6, we can find f(1).
By plugging the value of x=1
f(1) = f(0) + f(2) = 7
f(2) = f(1) + f(3)
f(3) = f(2) – f(1)
= 6 – 7
= −1
Also, f(3) = f(2) + f(4)
f(4) = f(3) – f(2) = −7
Continuing in a similar way, we can find out
f(0) = 1
f(1) = 7
f(2) = 6
f(3) = −1
f(4) = −7
f(5) = −6
f(6) = 1
f(7) = 7 and so on
After every 6 integral values of x, f(x) repeats itself.
f(6) = f(12) = f(18 ) = f(24) = f(30) = f(36) = f(42) = f(48 ) = 1
f(49) = 7
f(50) = 6
Example 2: If f(x) = 4x / (4x + 2)
Then find the value of f(1/100)+f(2/100)+ …+ f(99/100).
Solution: In these type of questions, an important observation has to be made regarding the pattern involved in the “required part”
(1/100 +99/100) = 1 and 99/100 = (1 -1/100) so f(x) and f(1-x) has a certain relation.
f (x) = 4x/4x + 2………(1)
f (1 – x) = 4(1 – x) / 4(1 – x) + 2. ……..(2)= 4/4 + 2.4x= 2/2 + 4x.On adding both the equations (1)and (2), we get
f(x) + f(1 – x) = [4x/4x + 2] + [2/4x + 2 ]= 1.Hence a generalisation is obtained,
f(1 / 100) + f(1 – 1/100) = f(1) + f(99/100) = 1.
f (2/100) + f( 1 – 2/100) = f(2) + f(98/100) = 1.
Similarly f(49/100) + f(50/100) = 1.
Hence f(1/100) + f(2/100) + f(3/100)………………………..f(99/100)
= 49.
|
121 videos|148 docs|111 tests
|
FAQs on Functions from Algebra: Basic Concepts and Application - Quantitative for GMAT
| 1. What are rational expressions and how are their graphs represented? |  |
| 2. How do piecewise functions differ from standard functions? |  |
| 3. What are transformations of graphs and how do they affect the shape of functions? |  |
| 4. What is the significance of identifying maxima and minima in applications? |  |
| 5. How do the greatest integer function and functions in remainders differ from typical functions? |  |