Important Formula: Percentages | Mathematics for RRB NTPC / ASM - RRB NTPC/ASM/CA/TA PDF Download
Percentage Formula
To determine the percentage, we have to divide the value by the total value and then multiply the resultant by 100. 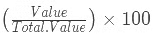

Formulas for Percentages & Definitions
- In mathematics, a percentage is a number or ratio expressed as a fraction whose denominator (bottom) is 100. Thus, x percent means x hundredths, written as x%.
We express x% as a fraction as x/100. - For example 10% = 10/100 = 1/10
Percentages Difference Formula
- When provided with two values and tasked with determining the percentage difference between them, this can be accomplished using the following formula:
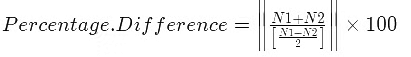
Formulas & Basic Concept of Percentages
- To calculate a % of b
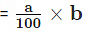
- To find what percentage of a is b
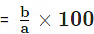
- To calculate percentage change in value
Percentage change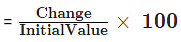
- Percentage Increase or Decrease
- Percentage increase
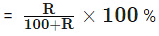
- Percentage decrease
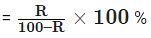
- Percentage increase
- Successive Percentage Change
If there are successive percentage increases of a % and b%, the effective percentage increase is:
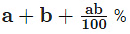
Results on population:
Let the population of a town be P now and suppose it increases at the rate of R% per annum, then:Population after n years
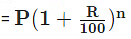
Population n years ago
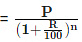
Results on Depreciation:
Let the present value of a machine be P. Suppose it depreciates at the rate of R% per annum. Then:Value of the machine after n years
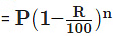
Value of the machine n years ago
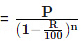
If A is R% more than B, then B is less than A by
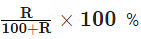
If A is R% less than B, then B is more than A by
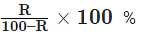
Increase N by S% :
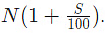
Decrease N by S%:
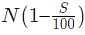
Q1: Peaches are now 50% more expensive at Reliance Smart Point. What percentage reduction in consumption is required to maintain peach expenditure constant?
(a) 35 %
(b) 35.50 %
(c) 33.33 %
(d) 32.50 %
Ans: (c)
If the price of a commodity increases by r%, then the reduction in consumption so as not to increase the expenditure is –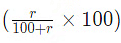 Therefore r is the increased price(i.e 50)By using the formula:
Therefore r is the increased price(i.e 50)By using the formula: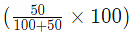

Q2: To pass the NDA Recruitment Test, candidates must receive 290 of the aggregate marks to pass. What is the highest total of marks an applicant can receive if they receive 203 and are considered unsuccessful by 12% of their total scores?
(a) 750
(b) 725
(c) 700
(d) 675
Ans: (b)
Let’s maximum aggregate marks = x
203 + 12% of x = 290
12% of x = 290 – 203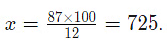
Q3: Raj invested ₹ 10000 in a fund. At the end of first year, he incurred a loss but his balance was more than ₹ 5000. This balance, when invested for another year, grew and the percentage of growth in the second year was five times the percentage of loss in the first year. If the gain of Raj from the initial investment over the two year period is 35%, then the percentage of loss in the first year is
(a) 5
(b) 15
(c) 17
(d) 10
Ans: (d)
Raj invested Rs 10000 in the first year. Assuming the loss he faced was x%.
The amount after 1 year is 10,000*(1 – x/100). = 10000 – 100*x.
Given the balance was greater than Rs 5000 and hence x < 50 percent.
When Raj invested this amount in the second year he earned a profit which is five times that of the first-year percentage.
Hence the amount after the second year is : 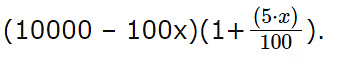 Raj gained a total of 35 percent over the period of two years and hence the 35 per cent is Rs 3500.Hence the final amount is Rs 13,500.
Raj gained a total of 35 percent over the period of two years and hence the 35 per cent is Rs 3500.Hence the final amount is Rs 13,500.
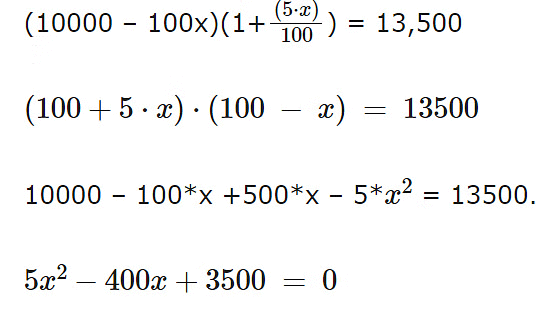
Solving the equation the roots are :
x = 10, x = 70.
Since x < 50, x = 10 percent.
Q4: Jason Statham could set aside 10% of his earnings. However, when his income increased by 20% two years later, he could only save the same amount as before. How much has his spending increased by percentage?
(a) 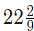 (b)
(b) 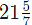 (c)
(c) 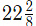 (d)
(d) 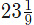 Ans: (a)
Ans: (a)
Let earlier income be 100 Rs
∴ Savings = 10% of 100 = 10 Rs
∴ Expenditure = 90 Rs
New Income = 120 Rs
Savings (same as before) = 10 Rs
∴ Expenditure = 120 – 10 = 110 Rs
∴ Increase in Expenditure = 110 – 90 = 20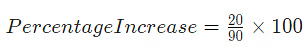
Q5: Robert Pattinson is an IT professional who spends 12% of his monthly income on power, 25% of his income on food, 20% of his income on his children’s education, 30% of his income on rent, and the rest 1040 on everything else. What is the person’s monthly salary?
(a) 7500 Rs
(b) 7700 Rs
(c) 7900 Rs
(d) 8000 Rs
Ans: (d)
Let the monthly salary of the Robert be x. then,
Total spends of Robert = (30 + 25 + 20 + 12) = 87%
Remaining % = 100 – 87 = 13%
So, 13% ≡ 1040
100% ≡ x
Using the cross multiplication method,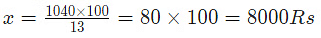
|
146 videos|113 docs|98 tests
|

















