Past Year Questions: Infiltration, Runoff and Hydrographs | Topic wise GATE Past Year Papers for Civil Engineering - Civil Engineering (CE) PDF Download
Q1: A storm with a recorded precipitation of 11.0 cm, as shown in the table, produced a direct run-off of 6.0 cm.
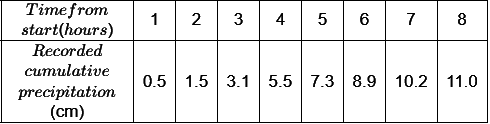
The ϕ-index of this storm is ____ cm/hr (rounded off to 2 decimal places) (2024 SET-2)
Ans: 0.64 to 0.65
Sol: Assume ϕ ≤ ilowest
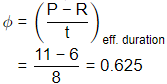Assume 0.625 < ϕ ≤ 0.8
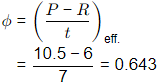
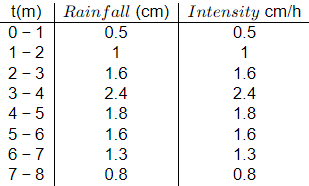
Q2: The ordinates of a 1-hour unit hydrograph (UH) are given below.
These ordinates are used to derive a 3-hour UH. The peak discharge (in m3/s ) for the derived 3-hour UH is ______(rounded off to the nearest integer). (2024 SET-1)
Ans: 86 to 88
Sol: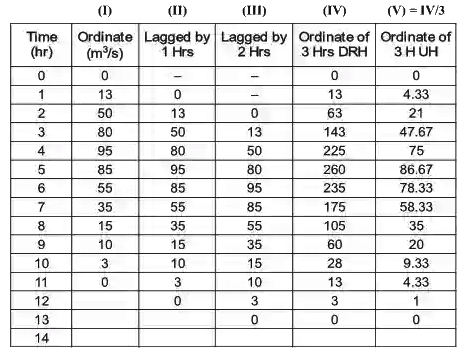 
Maximum ordinate of 3HUH is 86.67 m3/s
Maximum ordinate is 87 m3/s (to nearest integer)
Q1: Which one of the following options provides the correct match of the terms listed in Column-I and Column-II? (2023 SET-2)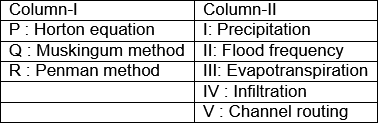
(a) P-IV, Q-V, R-III
(b) P-III, Q-IV, R-I
(c) P-IV, Q-III, R-II
(d) P-III, Q-I, R-IV
Ans: (a)
Sol: Horton's equation is used to calculate total infiltration.
Muskingum method is used in flood response analysis in channels.
Penman equation is used to calculate potential evapotranspiration.
Q2: In Horton's equation fitted to the infiltration data for a soil, the initial infiltration capacity is 10 mm/h; final infiltration capacity is 5 mm/h; and the exponential decay constant is 0.5 h. Assuming that the infiltration takes place at capacity rates, the total infiltration depth (in mm ) from a uniform storm of duration 12 h is ____. (round off to one decimal place) (2023 SET-1 )
Ans: 69.7 to 70.1
Sol: f0 = 10 meter
fc = 5 meter
K = 0.5hr−1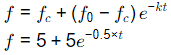
At capacity rates i.e. t→∞
f = 5 + 5e−0.5×∞
= 5 meters
Infiltration in 12hr. = 5 × 12 = 60 mm
If above is not the case :
then
Infiltration = ∫ fdt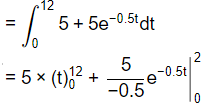
= 60 + 10 (1 - e0.5 x 12)
= 69.795 mm = 70 mm.
Q3: A 12-hour storm occurs over a catchment and results in a direct runoff depth of 100 mm. The time-distribution of the rainfall intensity is shown in the figure (not to scale). The ϕ-index of the storm is (in mmmm, rounded off to two decimal places)_____ (2023 SET-1)
Ans: 3.6 to 3.6
Sol: D = 12 hrs.
Direct runoff (R) = 100 mm = 10 cm
P = total rainfall
P = Area under above diagram
P = (1/2)×(12+2)×20
= 14 × 10 = 140 mm = 14 cm
Total Infiltration = Total rainfall − runoff
=140 − 100 = 40 mm
Assuming infiltration rate as x mm/hr.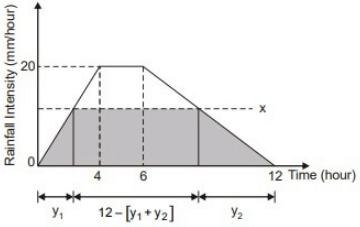
x/y1 = 20/4
y1 = x/5
y2 = x/y2 = 20/6
y2 = 3x/10
Total Infiltration
= Area under rainfall intensity duration curve Area of same curve below ϕ-index line.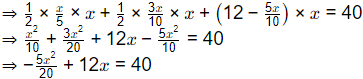
⇒x2−48x+160=0
⇒ x = 3.6 and x = 44.39 [Discarded]
⇒ ϕ = 3.6 mm/hr.
Q4: The ordinates of a one-hour unit hydrograph for a catchment are given below :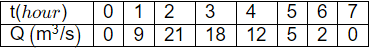
Using the principle of superposition, a D-hour unit hydrograph for the catchment was derived from the one-hour unit hydrograph. The ordinate of the D-hour unit hydrograph were obtained as 3 m3/s at t = 1 hour and 10 m3/s at t = 2 hour. the value of D (in integer) is _____ (2023 SET-1)
Ans: 3 to 3
Sol: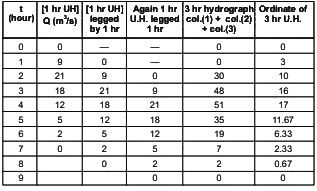 
Clearly seen
The duration D = 3 hours
Q1: A two-hour duration storm event with uniform excess rainfall of 3 cm occurred on a watershed. The ordinates of streamflow hydrograph resulting from this event are given in the table.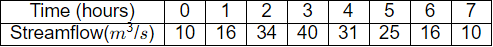
Considering a constant baseflow of 10 m3/s, the peak flow ordinate (in m3/s) of one-hour unit hydrograph for the watershed is ________ . (in integer) (2022 SET-1)
Ans: 12 to 12
Sol: C1 = Time
C2 = Ordinates of 2hr DRH
C3 = Ordinates of 2hr UH = (Ordinates of 2hr DRH)/(Rianfall excess of 3cm)
C4 = S-curve lag by 2hr
C5 = S-curve ordinates S2
C6 = S1 curve
C7 = Ordinates of 1hr UH = (S2−S−1)/1/2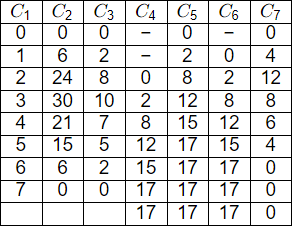
Q1: The hyetograph in the figure corresponds to a rainfall event of 3 cm.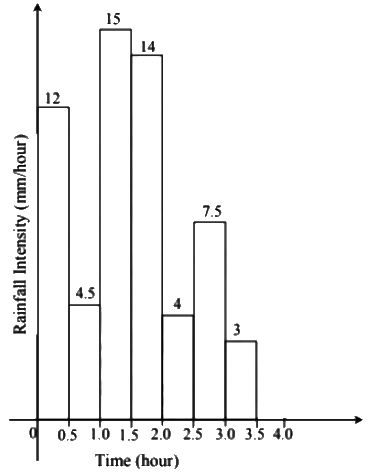
If the rainfall event has produced a direct runoff of 1.6 cm, the ϕ-index of the event (in mm/hour, round off to one decimal place) would be (2021 SET-2)
Ans: 4.2 to 4.2
Sol: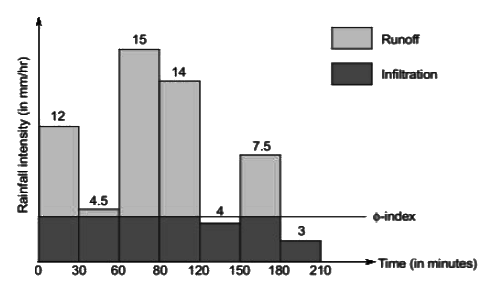 
Total rainfall = 3 cm
Total runoff = 1.6 cm
∴ Total infiltration = 3 − 1.6 = 1.4 cm
∴ W-index = Total infiltration /Total duration of storm
= 1.4/(210/60) cm/hr
= 0.4 cm/hr = 4 mm/hr
As ∅-index > W-index
Hence storm of intensities 4 mm/hr and 3 mm/hr will not produce rainfall exam.
ϕ -index = Total infiltration in which rainfall excess occur / Time period in which rainfall excess occur
= Total infiltration − Infiltration in which no rainfall excess occur / Texcess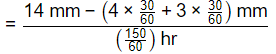
= 4.2 mm/hr
Q2: A 12-hour unit hydrograph (of 1 cm excess rainfall) of a catchment is of a triangular shape with a base width of 144 hour and a peak discharge of 23 m3/s. The area of the catchment (in km2, round off to the nearest integer) is _______ (2021 SET-2 )
Ans: 595 to 598
Sol: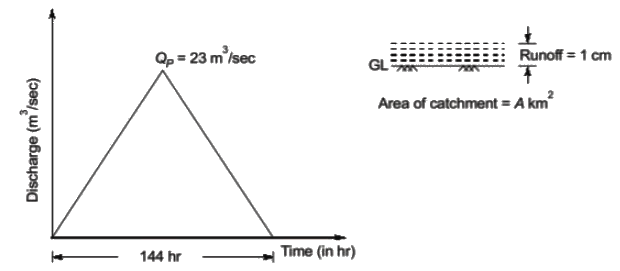 
Area of hydrograph = Total direct runoff volume
⇒ (1/2) × 23 m3/sec × 144 × 3600 sec= Area of catchment × Runoff depth
⇒ (1/2) × 23 x 144 x 3600 m3 = A x (1/100) m
A = 596.16 x 106 m2
∴ Area of catchment = 596.16 km2
Q3: The value of abscissa (x) and ordinate (y) of a curve are as follows: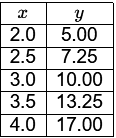
By Simpson's 1/3rd rule, the area under the curve (round off to two decimal places) is ______ (2021 SET-1)
Ans: 20 to 21
Sol: d = 0.5 unit
A = d/3 [(y1 + y5) + 4(y2 + y4) + 2y3]
= 0.5/3 [(5 + 17) + 4(7.25 + 13.25) + 2 × 10]
= 20.67 unit2
Q1: A triangular direct runoff hydrograph due to a storm has a time base of 90 hours. The peak flow of 60 m3/s occurs at 20 hours from the start of the storm. The area of catchment is 300 km2. The rainfall excess of the storm (in cm), is (2020 SET-2 )
(a) 2
(b) 3.24
(c) 5.4
(d) 6.48
Ans: (b)
Sol: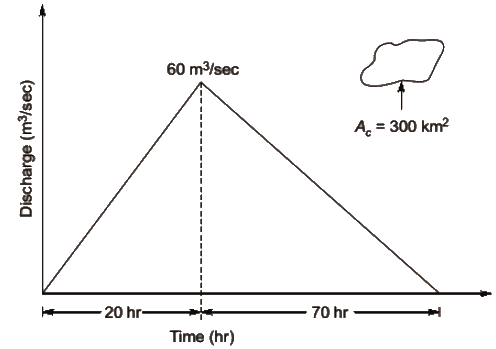 
Rainfall excess = 3.24 cm
Q2: The probability that a 50 year flood may NOT occur at all during 25 years life of a project (round off to two decimal places), is _______. (2020 SET-1)
Ans: 0.59 to 0.61
Sol: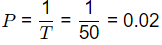
q = 1 - P = 0.98
∴ Probability of non-occurance of an event is given by
Assurance = qn
= (0.98)25
= 0.603
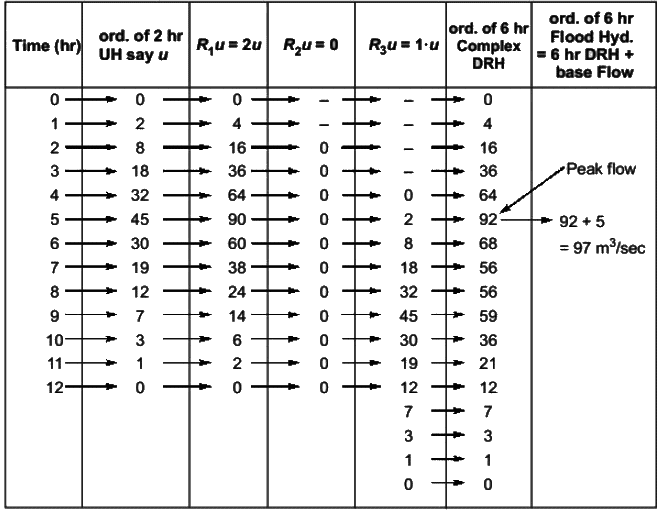
Q1: The ordinates, u, of a 2-hour unit hydrograph (i.e., for 1 cm of effective rain), for a catchment are shown in the table.
A 6-hour storm occurs over the catchment such that the effective rainfall intensity is 1 cm/hour for the first two hours, zero for the next two hours, and 0.5 cm/hour for the last two hours. If the base flow is constant at 5 m3/s, the peak flow due to this storm (in m3/s, round off to 1 decimal place) will be _____ (2019 SET-2)
Ans: 96.5 to 97.5
Sol: Rainfall excess in 1st two hours,
R1 = 1 cm/hr × 2hr = 2cm
Rainfall excess in 2nd two hours
R2 = 0
Rainfall excess in 3rd two hours,
R3 = 0.5 cm/hr × 2hr = 1cm
Q2: An inflow hydrograph is routed through a reservoir to produce an outflow hydrograph. The peak flow of the inflow hydrograph is PI and the time of occurrence of the peak is tItI. The peak flow of the outflow hydrograph is PO and the time of occurrence of the peak is tO. Which one of the following statements is correct? (2019 SET-2)
(a) PI < PO and tI < tO
(b) PI < PO and tI > tO
(c) PI > PO and tI < tO
(d) PI > PO and tI > tO
Ans: (c)
Sol: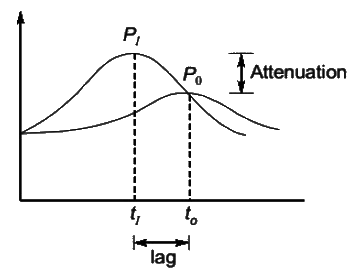 
The outflow from the reservoir is uncontrolled therefore peak of outflow hydrograph will occur at the junction of inflow and outflow hydrograph.
PI > P0
tI < t0
Q3: The hyetograph of a storm event of duration 140 minutesis shown in the figure.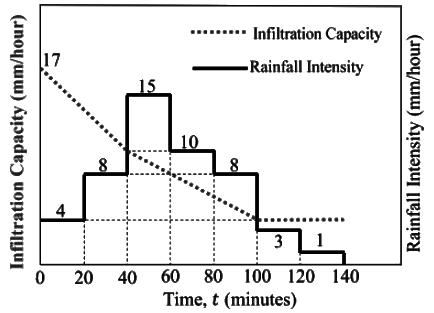
The infiltration capacity at the start of this event (t = 0) is 17 mm/hour, which linearly decreases to 10 mm/hour after 40 minutes duration. As the event progresses, the infiltration rate further drops down linearly to attain a value of 4 mm/hour at t = 100 minutes and remains constant thereafter till the end of the storm event. The value of the infiltration index, ϕ (in mm/hour, round off to 2 decimal places), is _______ (2019 SET-1)
Ans: 7 to 7.3
Sol: P = (4 + 8 + 15 + 10 + 8 + 3 + 1) × (20/60)
= 16.33 minute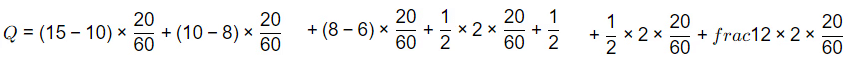
= 4mm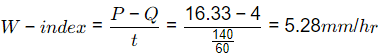
Since, ∅ ≥ W
Assume, ∅ = 5.28 mm/hr
⇒ Corrected, ∅ =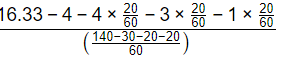 
= 7.2475 mm/hr
Q1: The total rainfall in a catchment of area 1000 km2, during a 6 h storm, is 19 cm. The surface runoff due to this storm computed from triangular direct runoff hydrograph is 1 × 108m3. The ϕindex for this storm (in cm/h, up to one decimal place) is ______ (2018 SET-2)
Ans: 1.5 to 1.5
Sol: Surface runoff = 1×108m3/1000×106m2 = 0.1 m = 10 cm
Total rainfall = 19 cm
Rainfall intensity = 19/6 = 3.167 cm/hr
w-Index = P − Q/t = Total Infiltration/Total duration of storm
∴ w−Index = (19-10)/6 = 1.5 cm/hr
As intensity of rainfall > w-Index
And rainfall intensity is uniform therefore ϕ-index = w-Index = 1.5 cm/hr.
Q2: The infiltration rate f in a basin under ponding condition is given by f = 30 + 10e−2t, where, f is in mm/h and t is time in hour. Total depth of infiltration (in mm, up to one decimal place) during the last 20 minutes of a storm of 30 minutes duration is ______ (2018 SET-1)
Ans: 11 to 12
Sol: Infiltration rate f(t) = 30 + 10e−2t
Total infiltration depth in time 10 min. to 30 min.
i.e., 0.166 hour to 0.5 hour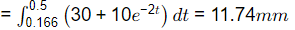
FAQs on Past Year Questions: Infiltration, Runoff and Hydrographs - Topic wise GATE Past Year Papers for Civil Engineering - Civil Engineering (CE)
| 1. What is infiltration in the context of hydrology? |  |
| 2. How is runoff calculated in civil engineering projects? | |
| 3. What is a hydrograph and why is it important in hydrology? | |
| 4. What factors affect the rate of infiltration in soils? | |
| 5. How do urbanization and land use changes impact runoff characteristics? | |
MCQs
,Runoff and Hydrographs | Topic wise GATE Past Year Papers for Civil Engineering - Civil Engineering (CE)
,Previous Year Questions with Solutions
,Past Year Questions: Infiltration
,Objective type Questions
,Runoff and Hydrographs | Topic wise GATE Past Year Papers for Civil Engineering - Civil Engineering (CE)
,Viva Questions
,Past Year Questions: Infiltration
,video lectures
,practice quizzes
,mock tests for examination
,Runoff and Hydrographs | Topic wise GATE Past Year Papers for Civil Engineering - Civil Engineering (CE)
,Summary
,shortcuts and tricks
,Extra Questions
,Exam
,Semester Notes
,Important questions
,Free
,Sample Paper
,study material
,past year papers
,ppt
,Past Year Questions: Infiltration
;
Past Year Questions: Infiltration, Runoff and Hydrographs Free PDF Download
Importance of Past Year Questions: Infiltration, Runoff and Hydrographs
Past Year Questions: Infiltration, Runoff and Hydrographs Notes
Past Year Questions: Infiltration, Runoff and Hydrographs Civil Engineering (CE)
Study Past Year Questions: Infiltration, Runoff and Hydrographs on the App
|
© EduRev
|
Education Revolution
|
|
