Overview: Quadratic Equations | CSAT Preparation - UPSC PDF Download
CSAT Angle
As per the CSAT point of view and the analysis of Previous Years’ Papers it has come to the notice that in the year 2023, two questions and in the years 2022-2016 one question each was asked from this chapter.
The topic ‘Elementary Algebra’ carries a great importance for CSAT exam, not only direct questions like solving an equation, finding the value of some components based on a given equation are asked but the basic concepts of formation of linear equation/quadratic equation is useful in topics like Average, Mensuration and Percentage, etc.
Polynomial is a Greek word formed with ‘Poly’ meaning ‘Many’ and ‘Nomial’ meaning ‘Terms’, so a polynomial is the combination of many terms together in a form of an expression or equation.
Polynomial
An expression of the form: f(x) = a0 + a1x + a2x2 + ... + anxn
where a0, a1, a2, ..., an are constants (real numbers), an ≠ 0, and n is a non-negative integer, is called a polynomial in variable x over reals.
The real numbers a0, a1, a2, ..., an are known as the coefficients of the polynomial.
If a0, a1, a2, ..., an are all integers, then we call it a polynomial over integers. If they are rational numbers, then we call it a polynomial over rationals.
e.g.
(i) 4x2 + 7x - 9 is a polynomial over integers.
(ii) 7/3x3 + 2/3x2 - 7/3 x + 5 is a polynomial over rationals.
(iii) 4x2 - √3x + √5 is a polynomial over reals.
Some important terms related to polynomials are defined as:
Monomial A polynomial having only one term, is called a monomial.
e.g. 7, 2x and 8x3 are monomials.
Binomial A polynomial having two terms, is called a binomial.
e.g. 3x + 4, 8x2 - 3x and x2 + 8 are binomials.
Trinomial A polynomial having three terms, is called a trinomial.
e.g. 7x2 - 3x + 8 is a trinomial.
Degree of a Polynomial
The exponent of the highest degree term in a polynomial, is known as its degree.
Types of polynomials
There are five types of polynominals as given below:
- Zero polynomial A polynomial of degree zero, is called zero polynomial.
e.g. f (x) = 8, f (x) = -5/2
The degree of zero polynomial is not defined. - Linear polynomial A polynomial of degree one, is called a linear polynomial. In general, f (x) = ax + b, where a ≠ 0 is a linear polynomial. e.g. f (x) = 3x − 7 is a linear polynomial as the highest degree of x is 1.
- Quadratic polynomial A polynomial of degree two, is called a quadratic polynomial. In general, f (x) = ax2 + bx + c, where a ≠ 0 is a quadratic polynomial. e.g. f (x) = x2 − 7x + 8 is a quadratic polynomial as the highest degree of x is 2.
- Cubic polynomial A polynomial of degree three, is called a cubic polynomial. In general, f (x) = ax3 + bx2 + cx + d , a ≠ 0 is a cubic polynomial. e.g. f (x) = 2x3 − x2 + 8x + 4 is a cubic polynomial as the highest degree of x is 3.
- Biquadratic polynomial A polynomial of degree four, is called a biquadratic polynomial. In general, f (x) = ax4 + bx3 + cx2 + dx + e, a ≠ 0 is a biquadratic polynomial. e.g. f ( x ) = 4x4 + 3x3 + 9x2 + 5x + 2 = 0 is a biquadratic polynomial as the highest degree of x is 4.
Zero of a Polynomial
A real number α is a zero (or root) of a polynomial f (x), if f (α ) = 0. e.g. If x = 1 is a root of the polynomial 3x3 + 2x2 + x - 2 , then f (1) = 0.
We have, f (x) = 3x3 − 2x2 + x − 2
∴ f(1)= 3 × 13 − 2 × 12 +1 − 2 = 3 − 2 + 1 − 2 = 0
Hence, x = 1 is a root of polynomial f ( x ).
- A polynomial of degree n has maximum n roots.
- A linear polynomial f(x ) = ax + b, where a ≠ 0, has a unique root given by x = -b/a
- Every real number is a root of the zero polynomial.
- A non-zero constant polynomial has no root.
Example: Find the types of the polynomial given below (on the basis of degree).
(i) 3x2+ 4x + 5
(ii) 3 + 3z + 4z4
Sol: (i) Here, the highest power of x in a given polynomial is 2. So, it is a quadratic polynomial.
(ii) Here, the highest power of z in a given polynomial is 4. So, it is a biquadratic polynomial.
Remainder Theorem
Let f(x) be a polynomial of degree greater than or equal to one and a be any real number. If f(x) is divided by (x - a), then the remainder is equal to f(a).
Example: Find the remainder when f(x) = 2x3 − 13x2 + 17x + 10 is divided by (x − 2).
(a) 8
(b) 9
(c) 10
(d) 12
Sol: (a) When f (x) is divided by (x − 2) , then remainder is given by
f(2) = 2(2)3-13(2)2 + 17(2) + 10
=16 - 52 + 34 + 10 = 8
Thus, dividing f (x ) = 2 x3 − 13x2 + 17x + 10 by x − 2 , we get the remainder equal to 8.
Factor Theorem
Let f (x) be a polynomial of degree greater than or equal to one and a be any real number such that f (a) = 0, then (x − a) is a factor of f (x). Conversly, if (x − a) is a factor of f (x), then f (a) = 0.
Example: Show that (x + 2) is a factor of the polynomial x2 + 4x + 4.
Sol: Let f (x) = x2 + 4x + 4, then (x + 2) = {x − (−2)} is a factor of f (x), if f (−2) = 0.
∴ f (−2) = (−2)2 + 4 (−2) + 4 = 4 − 8 + 4 = 0
Hence, (x + 2) is a factor of f (x ).
Important Formulas
- (x + y)2 = x2 + y2 + 2 xy
- (x − y)2 = x2 + y2 − 2 xy
- (x2 − y2) = (x + y) (x − y)
- (x + y + z)2 = x2 + y2 + z2 + 2 (xy + yz + zx)
- (x + y)2 + (x − y)2 = 2(x2 + y2)
- (x + y)2 − (x − y)2 = 4 xy
- (x − y)3 = x3 − y3 − 3xy (x − y)
- ( x + y)3 = x3 + y3 + 3 xy ( x + y)
- (x3 − y3)=(x− y)(x2 + y2 + xy)
- (x3 + y3) = (x + y)(x2 + y2 − xy)
- (x3 + y3 + z3 − 3 xyz) = (x + y + z) (x2 + y2 + z2 − xy − yz − zx)
- If x + y + z = 0, then x3 + y3 + z3 = 3 xyz
Linear Equations
When we equate two algebraic expressions, using the signs of equality, it forms an equation. A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and a single variable. Linear equations are first degree equations and may contain one or more variables. If the equation has only one variable, then the equation itself is sufficient to obtain the value of the variable and if the equation has two variables, then two consistent equations are required to get the value of the variables. In general, if an equation has n variables, then n consistent equations are required to obtain all the values of the n variables.
Linear Equation in One Variable
These are first degree equations with one unknown variable. An equation of the form ax + b = 0, where a , b ∈ R, where a ≠ 0 where x is the variable, is called a linear equation in one variable. There is only one variable x whose value is to be find out. e.g. ( x + 5) = 0 and ( y − 7) = 0 are linear equations in one variable in which we have to find the value of x or y based on equation.
Example. Verify that x = 2 is a solution of the linear equation 2x + 7 = 13 − x.
Sol: Given linear equation is 2x + 7 = 13 − x
On substituting x = 2 in the given equation, we get
LHS = 2× 2+ 7 = 4+ 7 = 11
RHS = 13 − 2 = 11
∴ LHS = RHS
Hence, x = 2 is a solution of the equation.
Linear Equation in Two Variables
These are first degree equations with two unknown variables. An equation of the form ax + by + c = 0, where a, b, c ∈R where a ≠ 0, b ≠ 0 and x, y are variables, is called linear equation in two variables. There are two variables x and y whose values are to be find out.
Any pair of values of x and y, which satisfy the equation ax + by + c = 0, is called its solution.
When two or more equations are satisfied by the same set of values of the variables involved in them, then they are termed as simultaneous equations.
Methods of Solving Two Simultaneous Linear Equations
The methods of solving two linear equations are given below:
Method of Substitution
- Step 1 Find the value of one variable (say y), in terms of the other i.e. x from either of the equation.
- Step 2 Substitute the value of y, so obtained in the other equation. Thus, we get an equation in one variable x.
- Step 3 Solve this equation for x.
- Step 4 Substitute the value of x, so obtained in Step 1 and find the value of y.
Example. Solve the equations x + y = 7, 3x − 2y = 11 and then find the values of x and y.
(a) x = 5, y = 2
(b) x = 2, y = 5
(c) x = 3, y = 1
(d) x = −1, y = 3
Sol: (a) Given equations are
x + y = 7 …(i)
and 3x − 2y = 11 …(ii)
From Eq. (i), y = (7 − x)
On substituting y = (7 − x) in Eq. (ii), we get
3x − 2 (7 – x) = 11
⇒ 3x − 14 + 2x = 11
⇒ 5x = 25
⇒ x = 5
On substituting the value of x in Eq. (i), we get
5 + y = 7
∴ y = 7 − 5 = 2
Hence, x = 5 and y = 2 is the required solution.
Method of Elimination
- Step 1 Obtain the two equations.
- Step 2 Multiply the equation, so as to make the coefficient of the variables, to be eliminated, equal.
- Step 3 Add or subtract the equations obtained in Step 2 according as the terms having the same coefficients are of opposite or of the same sign.
- Step 4 Solve the equation in one variable obtained in Step 3.
- Step 5 Substitute the value found in Step 4 in any one of the equations and find the value of the other variable.
- Setp 6 The values of the variable in Steps 4 and 5 constitute the solutions.
Shortcut Method of Solving Two Linear Equations (Cross-multiplication Method)
Let two equations be a1x + b1 y = c1 and a2 x + b2 y = c2.
Then, the solution is written as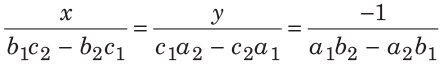
i.e.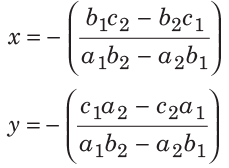 Types of linear equatient on the basis of solvability:
Types of linear equatient on the basis of solvability:
(i) Consistent system of equations A system of linear equations is said to be consistent, if it has a solution.
(ii) Inconsistent system of equations A system of linear equations is said to be inconsistent, if it has no solution.
Consistency of a System of Linear Equations
Consider the system of equations a1x + b1y + c1 = 0 and a2x + b2 y + c2 = 0
(i) There is a unique solution, if a1/b2 ≠ b1/b2
(ii) There are an infinite number of solutions, if
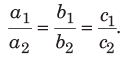
(iii) There is no solution, if
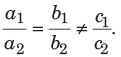
Example. Solve the equations x + 2y = 7, x − y = 1 and then find the values of x and y.
(a) 5, 4
(b) 1, 4
(c) 3, 2
(d) 3, 3
Sol. (c) By using the shortcut method of solving linear equation,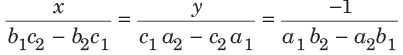 Here, a1 = 1 , b1 = 2, c1 = 7
Here, a1 = 1 , b1 = 2, c1 = 7
and a2 = 1 , b2 = − 1 , c2 = 1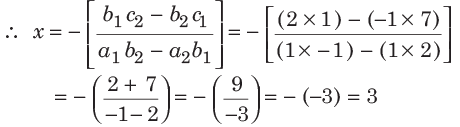 and
and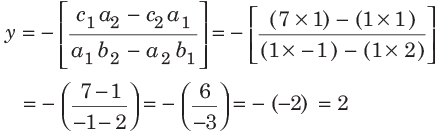
Hence, x = 3 and y = 2 is the required solution.
Quadratic Equations
The equations of the form ax2 + bx + c = 0, where a , b, c ∈ R and a ≠ 0, having highest degree equal to 2. Like a first degree equation in x, which has one value of x that satisfies the equation, a quadratic equation in x will have two values of x that satisfy the equation.
The values of x that satisfy the equation, are called the roots of the equation. These roots may be real or imaginary.
e.g. (i) x2 + 5x + 6 = 0 has roots x = −2 , − 3.
(ii) 15x2 − x − 28 = 0 has roots x = 7/5, -4/3.
(iii) x2 − 8 = 0 has roots x = 2√2, - 2√2
Method to Find the Roots of Quadratic Equations
In general, the roots of the quadratic equation can be found out by the following method :
1. By factorisation If the quadratic equation ax2 + bx + c = 0 can be expressed in the form (x − α) (x − β) = 0, then the roots of the equation are α and β.
Example. Find the possible value of the roots of equation x2 − 10x + 24 = 0.
(a) 4, 4
(b) 6, 4
(c) 6, 6
(d) 7, 6
Sol: (b) We have, x2 − 10x + 24 = 0
⇒ x2 − 6x− 4x + 24 = 0
⇒ x (x− 6) − 4 (x− 6) = 0
⇒ (x − 6) (x − 4) = 0
⇒ (x − 6) = 0 or (x − 4) = 0
∴ x = 6 or 4
2. Using direct formula If the quadratic equation is ax2 + bx + c = 0, then we can use the standard formula know as quadratic formula given below to find out the roots of the equation.
If α and β are the roots of the quadratic equation, then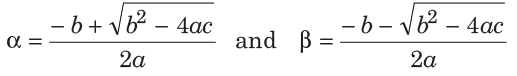
Also, b2 − 4ac = D (discriminant)
- We have, the discriminant, D = b2 − 4ac.
(i) If D < 0, then the roots α and β are imaginary.
(ii) If D > 0, then the roots α and β are real and distinct.
(iii) If D = 0, then the roots α and β are real and equal. - If D is a perfect square, then the roots are rational numbers.
- If D is positive but not a perfect square, then the roots are irrational number containing a radical.
Relationship between the Coefficients and Roots of a Quadratic Equation
Let ax2 + bx + c= 0 be a quadratic equation and α , β be the roots.
Then, sum of roots, and product of roots,
and product of roots,
If sum of the roots of the quadratic equation = (α + β ) and product of the roots of the quadratic equation = αβ
Then, the quadratic equation terms is
x2 − (α + β)x + αβ = 0
i.e. x2 − (Sum of roots)x + Product of roots = 0
(i) If a = c , then the roots are reciprocal of each other.
(ii) If c = 0, then one of the root is zero.
(iii) If c = − a, then the roots are negative reciprocal to each other.
(iv) If b = 0 and c = 0, then both roots are equal to zero.
(v) If a and c are of opposite signs, then the roots must be of opposite signs.
(vi) If b = 0, then the roots are negative of each other.
Solved Example
Example1: The degree of the following polynomial
p (x) = x3 + 1 + 2x = 6x + 1 /x is
(a) 2
(b) 4
(c) 3
(d) 5
Ans: (b)
Sol: 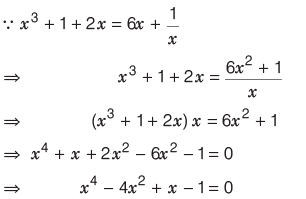
Hence, the degree of polynomial is highest exponent degree term i.e. 4.
Example2: Ramesh and Ganesh had some oranges initially. If Ramesh gave 5 oranges to Ganesh, then Ganesh will have thrice as many oranges as Ramesh. Instead of that, if Ganesh was to give 5 oranges to Ramesh, then they both will have the same number of oranges. Find the ratio of oranges that were distributed between Ramesh and Ganesh.
(a) 3 : 5
(b) 1 : 3
(c) 5 : 7
(d) 7 : 9
Ans: (a)
Let the number of oranges Ramesh has be x and the number of oranges Ganesh has be y.
Then, according to the first condition,
y + 5 = 3 (x − 5)
⇒ 3x − y − 20 = 0 ...(i)
According to the second condition,
x + 5 = y − 5
⇒ x − y + 10 = 0 …(ii)
On subtracting Eq. (ii) from Eq. (i), we get
2 x − 30 = 0
⇒ x = 15
On substituting the value of x in Eq. (ii), we get y = 25
∴ Ratio of oranges to be distributed between Ramesh and Ganesh = 15 : 25 = 3 : 5
|
205 videos|264 docs|136 tests
|
FAQs on Overview: Quadratic Equations - CSAT Preparation - UPSC
| 1. What is the degree of a polynomial and how is it determined? |  |
| 2. What are the different methods to solve two simultaneous linear equations? |  |
| 3. How does the cross-multiplication method work for solving linear equations? |  |
| 4. What is a quadratic equation and how can it be identified? |  |
| 5. What are the methods to solve quadratic equations? |  |
















